碎碎念

好久不更新，四月重新开始！

台大李宏毅机器学习作业——反向传播

Posted on Edited on In
Symbols count in article: 3.8k Reading time ≈ 3 mins.

严格来说不是课程的第四次作业，自己实现了一下全连接反向传播。

反向传播的原理在这一篇博客里面其实就已经大概讲过了，如果我们用的是sigmoid function作为激活函数，我们其实可以将每一层的一个神经元看做是一次逻辑回归。这里也不做太多解释，直接上代码。原本是想用MXNet实现的，但是MXNet和PyTorch都有自动求导函数，这样直接调用不利于深刻理解反向传播的具体过程，因此这里用numpy自己实现了一下。

首先定义自己的数据 

1
2
3
4
5
6
7
8
9
10
dataset = np.array([[2.7810836, 2.550537003, 0],
                    [1.465489372, 2.362125076, 0],
                    [3.396561688, 4.400293529, 0],
                    [1.38807019, 1.850220317, 0],
                    [3.06407232, 3.005305973, 0],
                    [7.627531214, 2.759262235, 1],
                    [5.332441248, 2.088626775, 1],
                    [6.922596716, 1.77106367, 1],
                    [8.675418651, -0.242068655, 1],
                    [7.673756466, 3.508563011, 1]])

这个数据集有十个样本，前面两列是feature，最后一列是y。

首先我们将一些零零散散的函数定义掉，比如说激活函数以及激活函数的导数，还有metric。这里使用了最经典的sigmoid作为激活函数，如果要用ReLu或者其他的都可以自己实现。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def sigmoid(weights, inputs):
    z = np.dot(inputs, weights)
    return 1 / (1 + np.exp(-z))


def sigmoid_derivative(weights, inputs):
    z = sigmoid(weights, inputs)
    return z * (1 - z)


def accuracy(y, y_hat):
    count = 0
    for i in range(len(y)):
        if y[i] == y_hat[i]:
            count += 1
    return count / len(y)

对于一个神经网络而言，实际上每一个隐藏层都是一组weight，因此我们定义一个函数来初始化隐藏层： 

1
2
3
def initialize_layer(num_features, num_hidden):
    weights = np.random.uniform(-0.1, 0.1, num_features * num_hidden).reshape((num_features, num_hidden))
    return weights

这个函数是按照指定的输入特征数量和指定的隐藏节点数量生成一个weight matrix。这里我没有加入bias，当然要加入也很简单。

然后我们知道，全连接，或者说神经网络其实都是两个步骤，第一步forward propagation，计算结果，第二部backward propagation将误差告诉给weight。所以我们先实现第一步的forward propagation。 

1
2
3
4
5
6
7
8
9
10
11
12
13
def forwark_propagate(network, inputs):
    outputs = []
    input_data = [inputs]
    outputs_derivative = []
    next_inputs = inputs
    for i in range(len(network)):
        output = sigmoid(network[i], next_inputs)
        output_d = sigmoid_derivative(network[i], next_inputs)
        outputs.append(output)
        input_data.append(output)
        outputs_derivative.append(output_d)
        next_inputs = output.copy()
    return outputs, outputs_derivative, input_data[:len(network)]
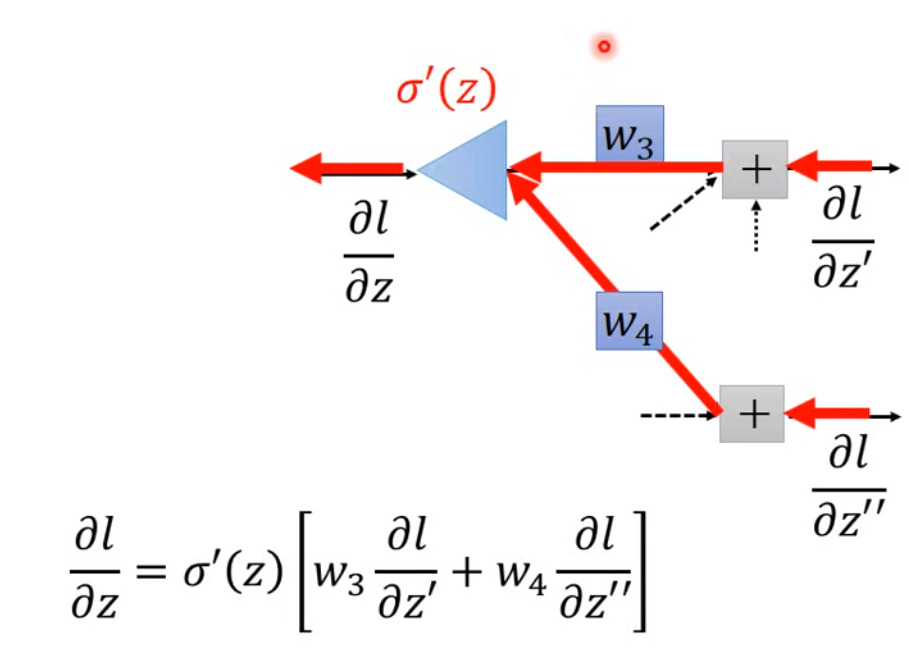
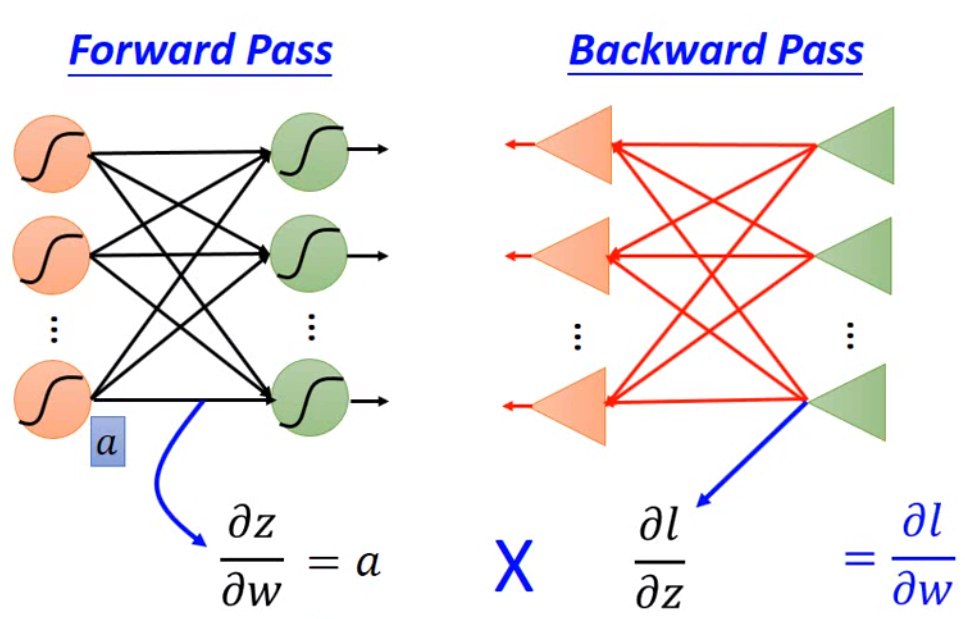
这里需要解释一下，我实现的比较绕，前馈的过程其实很简单，就是一个样本放进去，各种叉乘weight就好了，但是我们其实backward propagation需要用到很多中间过程的数据，回顾一下下面的过程：

我们可以看到，如果我们要计算第\(i\)层cost function对\(w\)的导数，我们需要用到第\(i\)层的输入以及激活函数的导数，第\(i+1\)层的weight和cost function对下一层\(z\)的导数。所以我将forward propagation过程中每一层的输入，每一层的输出，每一层activation derivative在输出的取值都保存下来。那实际上，上一层的输出就是下一层的输入。

然后我们实现一下反馈，也就是最核心的部分： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def backward_propagate(network, outputs, outputs_derivative, inputs, y_true):
    gradients = [1 for _ in range(len(network))]
    deltas = [1 for _ in range(len(network))]
    for i in reversed(range(len(network))):
        if i == len(network) - 1:
            delta = -(y_true - outputs[i].flatten())
            delta = delta.reshape(outputs[i].shape)
            deltas[i] = delta
            gradient = np.dot(inputs[i].T, delta)
            gradients[i] = gradient
        else:
            delta = outputs_derivative[i] * np.dot(deltas[i + 1], network[i + 1].T)
            deltas[i] = delta
            gradient = np.dot(inputs[i].T, delta)
            gradients[i] = gradient
    return gradients

这里我写的也还是有点绕，因为最后一层输出层是比较特殊的层，我们如果将这里看做是一个逻辑回归，那么我们就可以用之前逻辑回归推的方法，直接算出这一层的权重，然后就会发现，原本后面那个\(\sigma'(z)[w_3 \frac{\partial l}{\partial z'} + w_4 \frac{\partial l}{\partial z''}]\)其实就是\(-(y_{true} - y_{predict})\)，然后我们一样的，将每一层的导数存下来。这样我们就把核心的部分全部实现了。然后就是试一下能不能跑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
network = []
# network.append(initialize_layer(2, 1))
network.append(initialize_layer(2, 4))
network.append(initialize_layer(4, 1))

for epoch in range(20):
    output, output_d, inputs = forwark_propagate(network, dataset[:, :2])
    gradients = backward_propagate(network, output, output_d, inputs, dataset[:, 2])
    for i in range(len(network)):
        network[i] -= 0.1 * gradients[i]
    res = []
    for i in output[len(network) - 1]:
        if i < 0.5:
            res.append(0)
        else:
            res.append(1)
    print('Epoch %s, Accu %.2f%%' %(str(epoch), accuracy(dataset[:, 2], res)*100))

结果如下

Epoch 0, Accu 50.00%
Epoch 1, Accu 50.00%
Epoch 2, Accu 70.00%
Epoch 3, Accu 100.00%
Epoch 4, Accu 100.00%
Epoch 5, Accu 100.00%
Epoch 6, Accu 100.00%
Epoch 7, Accu 100.00%
Epoch 8, Accu 100.00%
Epoch 9, Accu 100.00%
Epoch 10, Accu 100.00%
Epoch 11, Accu 100.00%
Epoch 12, Accu 100.00%
Epoch 13, Accu 100.00%
Epoch 14, Accu 100.00%
Epoch 15, Accu 100.00%
Epoch 16, Accu 100.00%
Epoch 17, Accu 100.00%
Epoch 18, Accu 100.00%
Epoch 19, Accu 100.00%

当然，如果只有一层的话就是最普通的逻辑回归，效果也差不多。另外这样一个tiny fc可以试试看learning rate对结果的影响，效果非常明显。