深度学习入门介绍,主要是MLP
深度学习本身不是很复杂的模型,只是机器学习的一个子分支,就是神经网络的加深加宽版本。当然,这么说也不完全对,不过深度学习的基础还是神经网络。
最早的时候深度学习就是 MLP 或者就叫神经网络,但是因为种种历史原因,早年间这种方法死活干不过 SVM,所以只能改名重出江湖。这其中各种恩怨情仇很八卦。
当然,后来 MLP 改名深度学习之后就重出江湖了,在 ImageNet 这个大赛上一举夺冠之后就一发不可收拾了。
深度学习其实就是机器学习的一个子分支,因此深度学习也满足机器学习的一般流程:提出假设模型,计算模型好坏,选择表现最好的模型。对于深度学习而言,模型就是神经网络。
一般最基础的深度学习模型就是全连接,也就是 Fully Connect Feedforward Network,如下图。
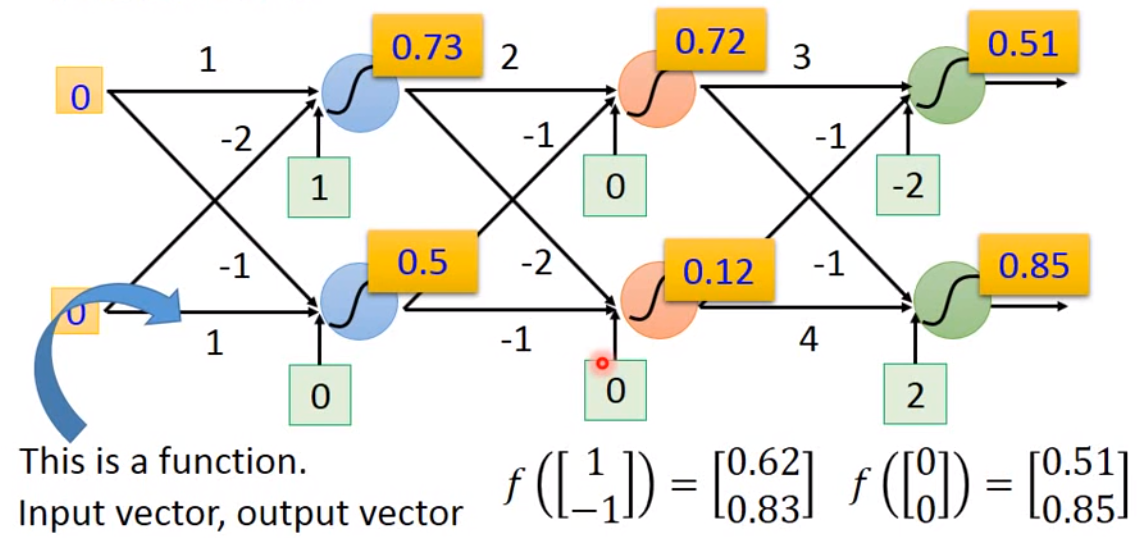
这个神经网络的基本工作流程就是输入一个向量,乘以不同的系数,再将结果用 sigmoid 函数输出到下一层作为输入。这里每一个神经元都是一个函数,我们叫做激活函数。现在的神经网络设计中,sigmoid 函数已经很少用了,比较常用的是 ReLu 或者 tanh。
一个常见的神经网络可以分为输入层(Input Layer),隐藏层(Hidden Layer)以及输出层(Output Layer),基本结构如下:
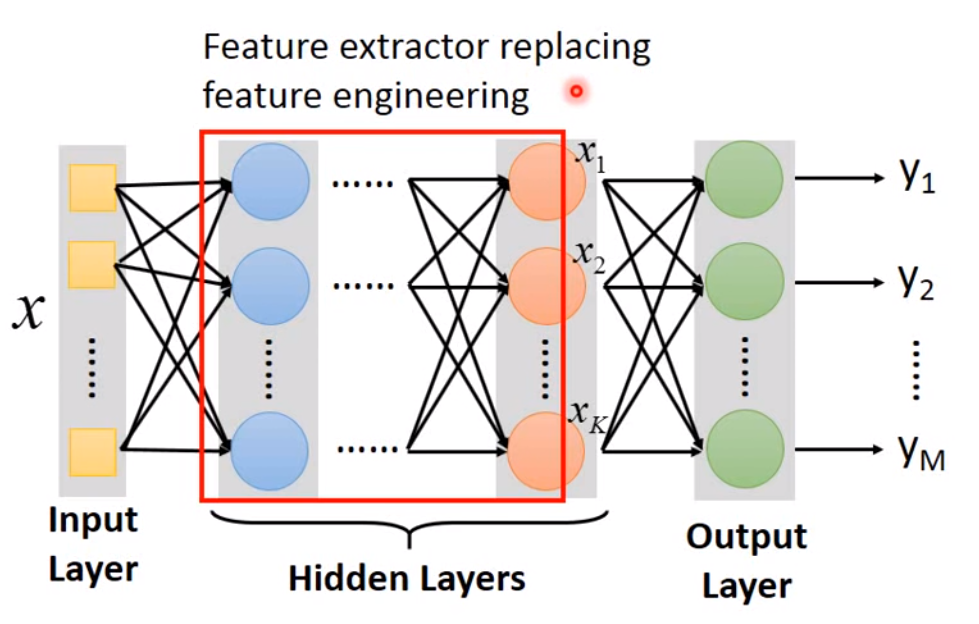
所以深度学习这边的模型假设就是设计神经网络结构,包括网络层数,每层的神经元数量等等。
其他的部分,设计 Loss function 和其他机器学习方法并没有什么本质区别,多分类一样可以用交叉熵,回归一样可以用 MSE。求解方法也是用梯度下降。
从理论上而言,只要有一个隐藏层就可以拟合任何连续函数。那么为什么我们要设计 Deep Learning 而不是 Fat Learning 呢?事实上,虽然理论上多层神经网络的表达能力和单层神经网络一样,但是在实操中,单层神经网络效果不如多层神经网络。
在之前的课程中,梯度下降需要求导的函数是比较简单的,现在多层神经网络要如何求导呢?神经网络本质上就是一个向量乘以多个矩阵,再经过激活函数进行变换。因此这里需要使用到链式求导:
如果\(y=g(x), z=h(y)\),则 \(\frac{d z}{d x} = \frac{d z}{d y} \frac{d y}{d x}\)
如果\(x=g(s), y=h(s), z=k(x, y)\),则\(\frac{d z}{d s} = \frac{\partial z}{\partial x} \frac{d x}{d s} + \frac{\partial z}{\partial y} \frac{d y}{d s}\)
这样我们就可以想办法对神经网络进行求导。神经网络求系数的方法叫做 Backpropagation。假设我们这里要对多分类问题进行求导,我们整个模型的 loss function 定义为\(L(\theta) = \sum_{n=1}^N l_n(\theta)\),每一个 \(l\) 是每个小分类的交叉熵。因此我们要求的就是\(\frac{\partial L(\theta)}{\partial w} = \sum_{n=1}^N \frac{\partial l_n(\theta)}{\partial w}\)。
我们拿一个 neuron 来分析:
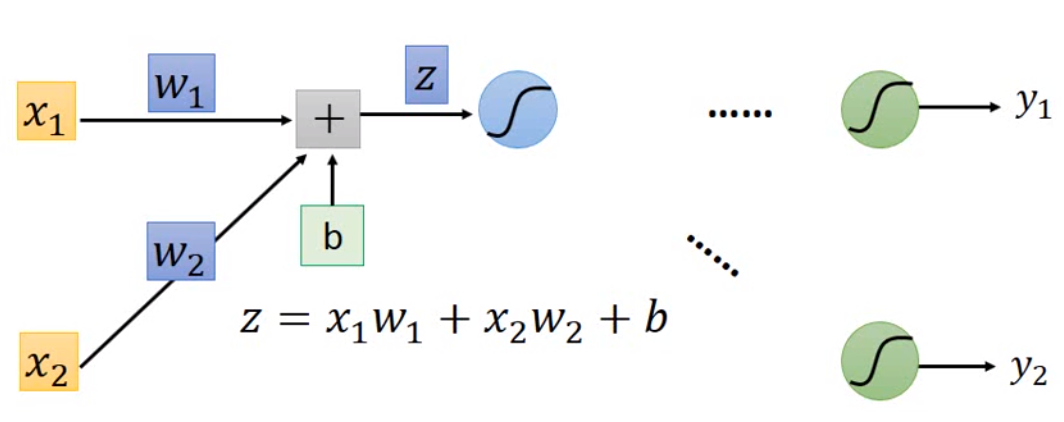
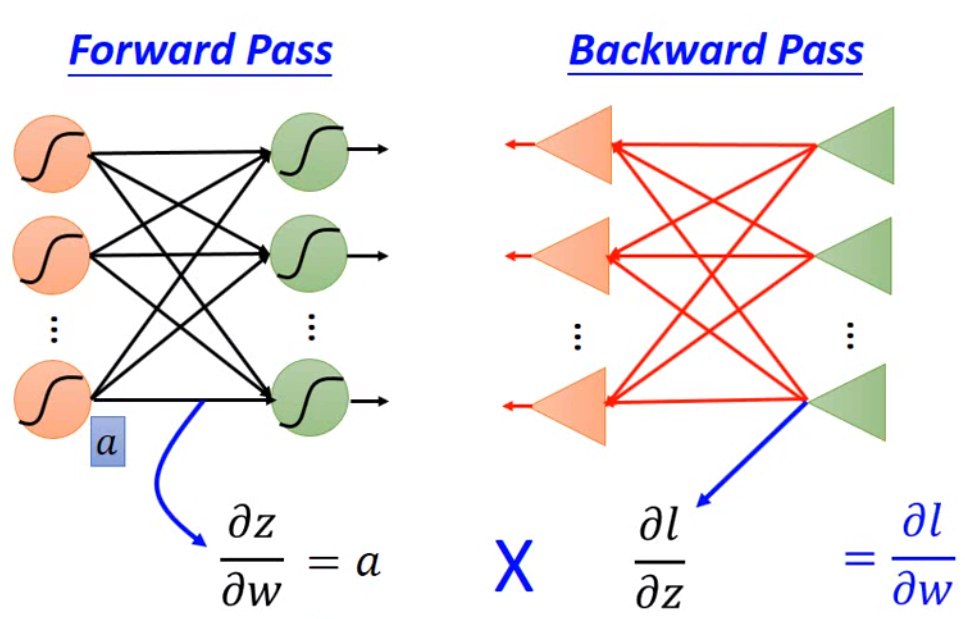
那基于链式求导,我们可以知道,我们要求的是\(\frac{\partial l_n(\theta)}{\partial w}\),那么可以拆解为\(\frac{\partial z}{\partial w} \frac{\partial l_n(\theta)}{\partial z}\)。因此Backpropagation 分为两个步骤,一个是 Forward(\(\frac{\partial z}{\partial w}\)),一个是 Backward(\(\frac{\partial l_n(\theta)}{\partial w}\))。
首先是 Forward 部分,我们要计算\(\frac{\partial z}{\partial w}\),这个其实很好算,就是这一层的 input。
最后是 Backward 部分。我们假设 \(a = \sigma(z)\):
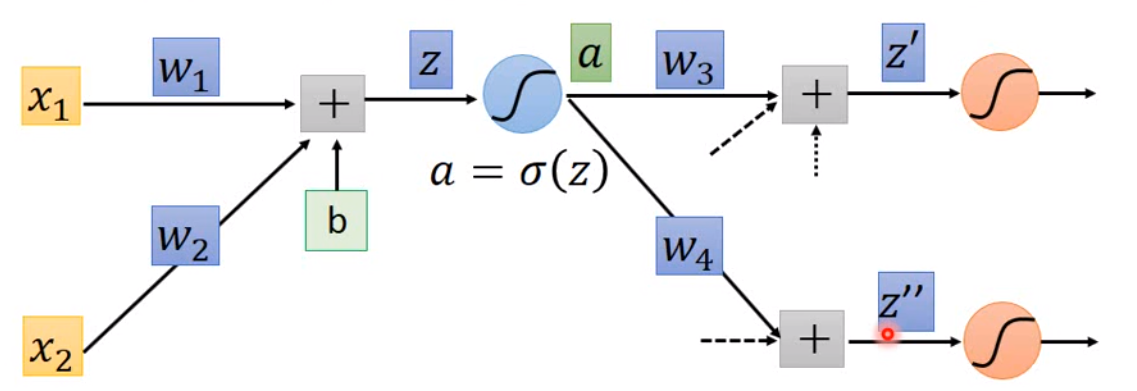
那么\(\frac{\partial l}{\partial z} = \frac{\partial a}{\partial z} \frac{\partial l}{\partial a}\),而因为\(a\)会影响后面的参数,因此 \(\frac{\partial l}{\partial a} = \frac{\partial z'}{\partial a} \frac{\partial l}{\partial z'} + \frac{\partial z''}{\partial a} \frac{\partial l}{\partial z''}\)。那事实上,\(\frac{\partial z'}{\partial a}\)就是\(w_3\),其他相应可以算出来。如下图:
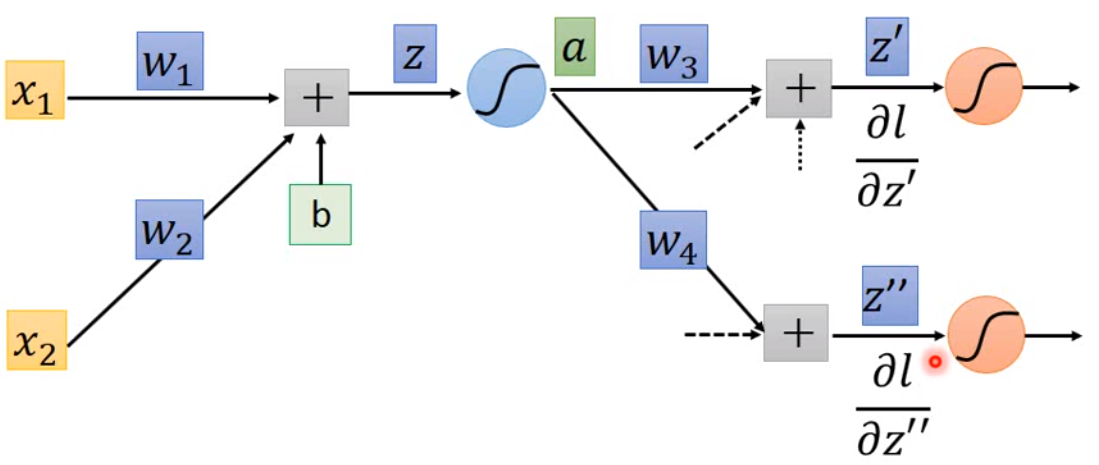
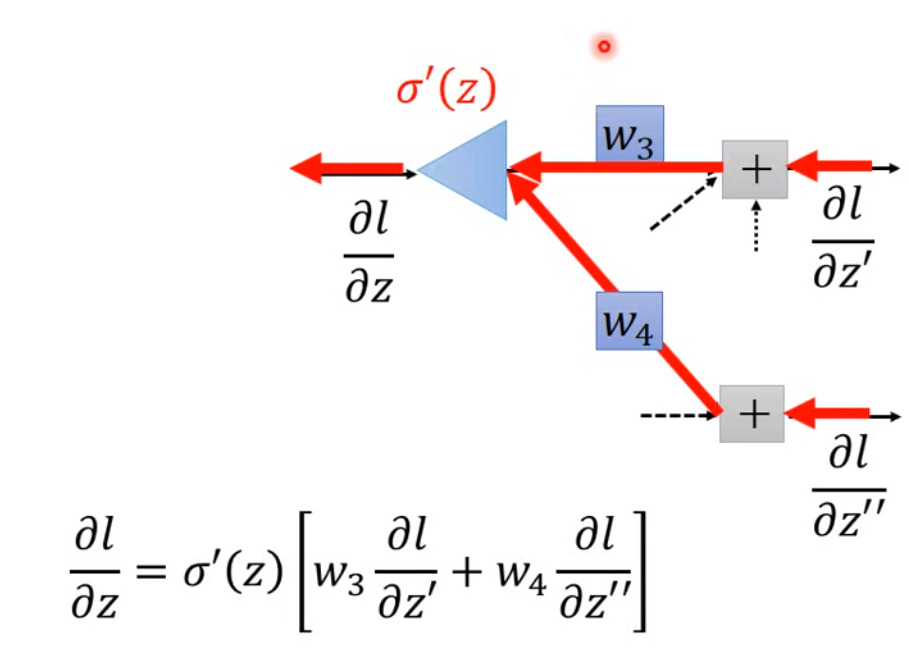
我们现在假设\(\frac{\partial l}{\partial z'}\)和\(\frac{\partial l}{\partial z''}\)已知,那么\(\frac{\partial l}{\partial z} = \sigma'(z)\Big[w_3 \frac{\partial l}{\partial z'} + w_4 \frac{\partial l}{\partial z''} \Big]\),这里用\(\sigma'(z)\)表示激活函数的导数。因此我们也可以将这个方程看成另一个类似神经网络的结构:
如果这就是最后的output layer,那么\(\frac{\partial l}{\partial z'} = \frac{\partial y_1}{\partial z'} \frac{\partial l}{\partial y_1}\),其他同理可求。
如果这不是output layer,就一直算,一直算到最后的output layer。这样的方法计算量似乎非常大,那么为了提高运算效率,我们可以从output向前计算。所以整个的解法大概如下: