深度学习入门——常见网络结构
全连接网络
深度学习讲到底其实就是个各种神经网络的变种。最基础的神经网络结构就是全连接层。全连接就是上一层的神经元都与下一层的神经元相互连接。这样的网络结构看上去就像下面的图一样：
那出于方便的考虑，我们这样声明一个权重\(w_{ij}^l\)这里的上标\(l\)用来表示第\(l\)层的神经元，而下标\(j\)表示起始的位置，而\(i\)表示结束的位置。这样的定义实际上是为了看起来方便。原因是，我们将\(z_1^l\)拆开来看，可以表达为\(z^l_1 = w_{11}^{l}a^{l-1}_1 + w_{12}^{l}a^{l-1}_2 + \cdots + w_{1n}^{l}a^{l-1}_n\)。如果我们将\(z^l_i\)表示为一个向量，这样就能得到一个权重的矩阵。我们将这个表示如下： \[ \begin{bmatrix} z^l_1 \\ z^l_2 \\ \vdots \\ \end{bmatrix} = \begin{bmatrix} w^l_{11}, &w^l_{12}, &\cdots \\ w^l_{21}, &w^l_{22}, &\cdots \\ \vdots, &\vdots, &\ddots \\ \end{bmatrix} \begin{bmatrix} a^{l-1}_1 \\ a^{l-1}_2 \\ \vdots \end{bmatrix} + \begin{bmatrix} b^l_1 \\ b^l_2 \\ \vdots \end{bmatrix} \] 由于我们之前的下标定义方式是输入层在后，输出层在前，因此我们的权重矩阵看上去是这样的，那么这样我们将这个公式简写成上图中的格式的时候\(W^l\)就不需要转置。如果下标定义跟上文的定义相反，采用输入层在右边，输出层在左边的方法，那么这里的权重矩阵就需要做一个转置。
循环神经网络（Recurrent Neural Network）
循环神经网络有多种多样的变形，最基本的深度循环神经网络的结构如下： 
一个循环神经网络由这样一个个的block组成。每一层的block用的是同样的function。每个function接受同样两个输入，同时有两个输出，表示为\(h, y = f(h, x)\)。
一个深度循环神经网络是需要将上一轮的\(y\)作为下一层的输入的，因此他们的dimension必须是一致的。
Naive RNN
最简单的RNN结构就是上图的样子，每一个block有两个输入两个输出。计算的逻辑是： \[ h' = \sigma(W^h h + W^i x) \\ y = \sigma(W^o h') \] 这里如果我们需要输出概率，也可以将sigmoid激活函数改成softmax。另外这里的\(W^o\)指的是output weight。
最简单的RNN结构也可以是双向的： 
LSTM
LSTM是RNN的一个变种，也是目前主流的RNN基本结构。LSTM的结构比naive RNN复杂一些。简化的block如下图：
LSTM之所以被叫做是有memory的网络，是因为这里的两个参数\(c和h\)更新速度是不是一样的。
\(c\)的更新速度比较慢，通常\(c^t\)就是\(c^{t-1}\)加上某一个值，因此这里可以有很长时间的记忆。也就是long term的memory。
而\(h\)的更新速度比较快，前后两个阶段的\(h\)可以毫无关系。因此这里就是short term的memory。
这样一个复杂的block的计算方法是这样的，首先我们将\(x^t和h^{t-1}\)拼成一个很大的vector，我们为了方便考虑这里就记做\(V\)。首先我们做四个计算： \[ z = \tanh(WV) \\ z^i = \sigma(W^i V) \\ z^f = \sigma(W^f V) \\ z^o = \sigma(W^o V) \] 计算这四个值是因为扒开LSTM的block，一个block除了对输入做activate，还有三个gate，分别是input gate，forget gate和output gate。大概的结构如下：
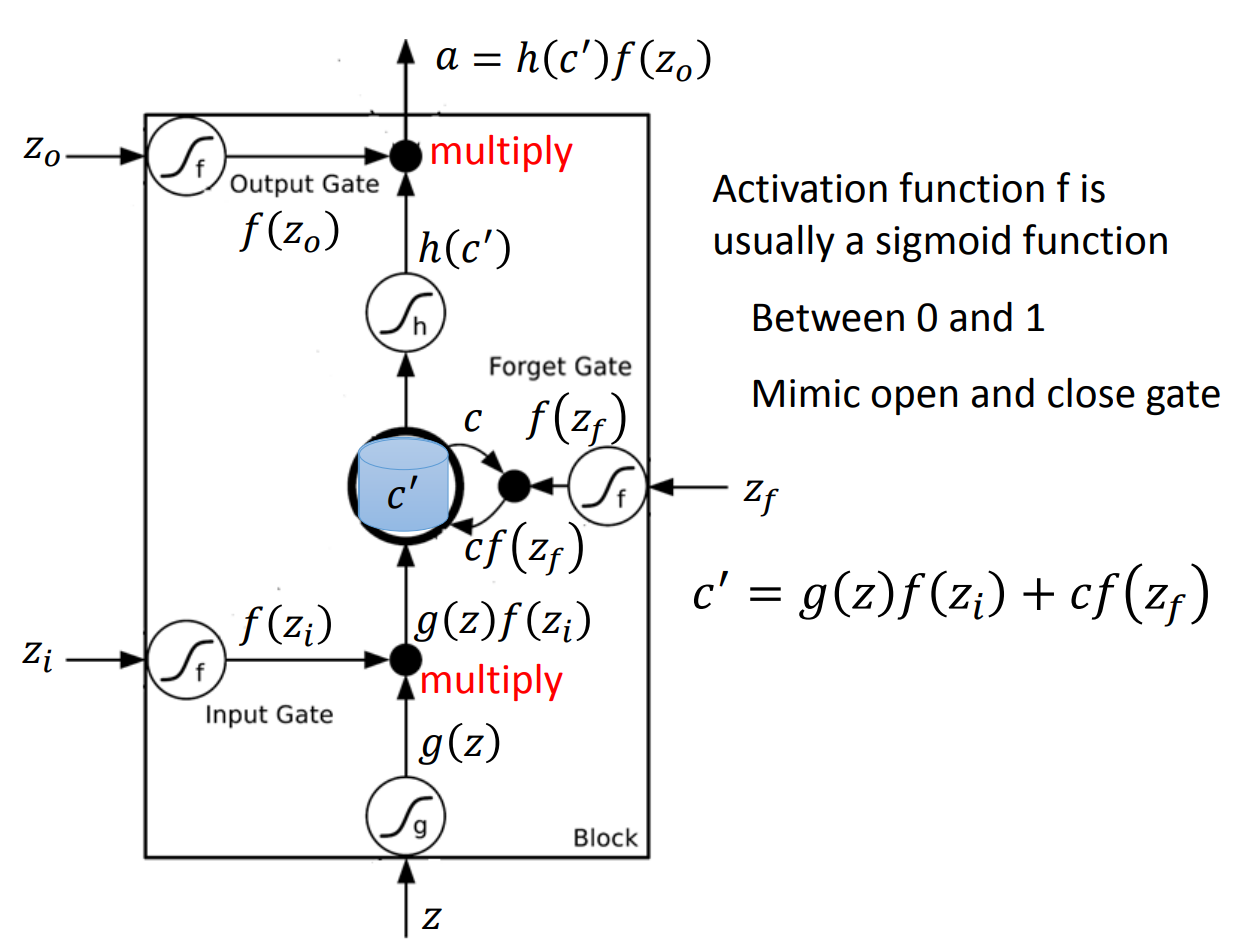
具体的一个计算过程可以看之前的一篇博客。这篇博客里有一个toy LSTM的分步计算过程。
另外还有一种做法是将\(c\)跟\(x和h\)一起拼成一个更大的vector，[x, h, c]这样的顺序。然后我们可以看到其实我们前面计算的大weight matrix可以看做是三个部分的权重，分别对应这三块。一般而言，我们会要求对应\(c\)这部分的权重是diagonal的，原因是参数过多可能会过拟合，因此我们会希望这部分额外加入的部分尽量参数简单一些。这个过程我们叫做peephole。
这些计算完成以后，我们就要计算三个输出： \[ c^t = z^f \odot c^{t-1} + z^i \odot z\\ h^t = z^o \odot \tanh(c^t) \\ y^t = \sigma(W' h^h) \] 这里都是elementwise的乘法。
我们计算完成之后的三个输出就可以作为下一个block的输入继续计算。
GRU
GRU可以看做是对LTSM的一个简化版本。不同于LSTM还需要更新\(c\)，GRU不需要这部分的参数，因此需要更新的参数量较LSTM少了很多，可以更快计算完成。GRU简化的block如下：
这个结构是比较简单的，跟naive RNN一样只有两个输入两个输出。GRU的计算逻辑是这样的，首先一样将\(x^t和h^{t-1}\)合并为一个大vector，还是记做\(V\)，然后计算 \[ z^u = \sigma(W^u V) \\ z^r = \sigma(W^r V) \\ h' = \sigma(W' (h^{t-1} \odot z^r)) \] 这里的\(r和u\)分别代表GRU里面的reset和update。然后我们开始计算两个输出： \[ h^t = z^u \odot h^{t-1} + (1-z^u) \odot h' \\ y = \sigma(W h^t) \]
所以在GRU中，reset gate其实是给过去longterm的memory给一个权重。
卷积网络（Convolution Neural Network）
和RNN不一样的，RNN主要用在NLP领域，而CNN则在图像领域大放异彩。
实际上卷积网络是一个对全连接层的特殊简化版本，关于卷积网络可以参考之前的另一篇博客。这篇博客将基本原理讲的比较清楚，这里就不做更多阐述。
