暌违一年的更新, 最近用到NER相关的算法,简单记录一下,主要是HMM和CRF。感觉概率图比较牛逼。
NER发展
NER是NLP里面一个非常基础的任务,从NLP的处理流程上看,NER可以看做是词法分析中未登录词的一种。同时NER也是关系抽取、事件抽取、知识图谱、机器翻译、问答系统等诸多NLP任务的基础。一般而言NER主要是识别人们、地名、组织机构等,常见的NER算法大赛就是这样。实际上任何我们想要的特殊文本片段都可以认为是实体。比如价格、产品型号等。
NER的发展基本上是四个阶段,最初是基于规则和字典的方法,依赖专家构建复杂的词库,通过分词器和正则表达式等方式抽取。第二阶段就是以HMM和CRF为代表的机器学习时代,第三阶段是CNN+CRF或者RNN+CRF的方式,第四阶段也就是现在基本上是半监督或者Attention等深度学习方法。
马尔科夫链
一般而言,我们假设\(X\)是一个随机数据集合\(\{X_1, X_2, \ldots, X_t\}\),这些值源自状态集合\(S=\{s_1, \ldots, s_N\}\)。一个马尔科夫链满足下面两个条件: \[ \begin{matrix} P(X_{t+1} = s_k|X_1,\ldots,X_t) = P(X_{t+1} = s_k|X_t) & \text{Limited horizon} \\ P(X_2=s_k|X_1=s_j) = P(X_{t+1} = s_k|X_t = s_j), \forall t,k,j & \text{Time invariant} \end{matrix} \] 一个马尔科夫链会有一个转移矩阵来表示从每一个状态转移到下一个状态的概率,同时有一个初始概率来表示第一个时刻每个状态的概率。假设我们有两个状态0和1,有一个转移矩阵: \[ \begin{array} {|c|c|c|} \hline \ & 0 & 1 \\ \hline 0 & 0.3 & 0.7 \\ \hline 1 & 0.6 & 0.4 \\ \hline \end{array} \] 初始概率\(P(S = 0)=0.2, P(S=1)=0.8\),那么对于序列1011,我们就可以很容易算出来概率是\(0.8 \times 0.6 \times 0.7 \times 0.4=0.1344\)
HMM
那么隐马尔可夫又是什么呢?上面的马尔科夫是一个可以直接观测到的状态转移序列。那么现在存在一种序列,表面上是我们可以观测到的随机序列,但是背后却有我们无法得知的隐藏序列来生成这一个序列。比如恋爱的经典笑话。 1
2
3
4
5
6
7
8
9
10
11
12
13
14男:你怎么了?
女:没事。
男:你真的没事?
女:真的,你睡吧。
男:你确定没事?
女:真的。
男:好吧,那我睡了。
转头女的发了朋友圈,终究还是一个人扛下了所有。
男:到底发生了什么。
女:没事。
男:你不说我没法睡觉。
女:你睡你的。
男:好吧。
女的发了第二条朋友圈,果然还是没有人理解我。
一个HMM有两个序列,一个是观测序列\(O\),一个是隐藏序列\(H\)。HMM要满足以下假设: \[ \begin{cases} P(H_t=h_t|H_{1:t-1}=h_{1:t-1}, O_{1:t} = o_{1:t}) = P(H_t=h_t | H_{t-1} = h_{t-1}) & \text{Markovinanity} \\ P(O_t = o_t|H_{1:t} = h_{1:t}, O_{1:t-1}=o_{1:t-1}) = P(O_t=o_t|H_t=h_t) & \text{Output independence} \\ P(H_t=j|H_{t-1}=i) = P(H{t+s}=j|H_{t+s-1}=i), \forall i,j \in H & \text{Stationarity} \end{cases} \]
一个完整的HMM包含三个要素,transition matrix \(A\),emission matrix \(B\),还有初始状态分布概率\(\Pi\),可以将HMM表示为\(\lambda = (A, B, \Pi)\)。
那么HMM就有三个问题需要解决,一个是概率计算问题,也就是likelihood,第二个是参数学习问题,第三个是序列的解码问题。
HMM likelihood
要计算一个HMM生成序列的概率,首先想到的就是暴力解法,穷举所有可能状态的组合,那么通过暴力运算就可以将所有的可能性算出来。但是暴力运算的问题在于计算复杂度过高,复杂度达到\(O(TN^T)\)。所以一般解法有两种,一种是前向算法,另一种是后向算法。
前向算法的过程很简单,首先初始化各个状态下在时间1时候观测状态为o_1的概率,\(\alpha(i) = \pi_i b_i(o_1)\),然后递归求解,\(\alpha_{t+1}(j) = \Big[ \sum\limits_{i=1}^N \alpha_t a_{ij} \Big] b_j(o_{t+1})\),最后到了\(T\)时刻,\(P(O|\lambda) = \sum\limits_{i=1}^N \alpha_T(i)\)。这样的话复杂度就降低到了\(O(TN^2)\)的水平。因为每次只计算两个时刻之间的所有可能性。
这里演示一个简单的前向算法计算过程,假设有红白两种颜色的球,分别有三个盒子。我们可以观测到的球的颜色,隐藏的是球来自哪个盒子。初始概率\(\Pi = (0.2, 0.4, 0.4)\),transition matrix \(A = \begin{bmatrix} 0.5 & 0.2 & 0.3 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.3 & 0.5 \end{bmatrix}\),emission matrix \(\begin{bmatrix}0.5 & 0.5 \\ 0.4 & 0.6 \\ 0.7 & 0.3 \end{bmatrix}\),观测到的序列是\(O=\{红,白,红\}\),所以分步计算如下:
第一步,初始化。 \[\alpha_1(1) = \pi_1 b_1(o_1) = 0.2 \times 0.5 = 0.1, \ \alpha_1(2) = \pi_2 b_2(o_1) = 0.4 \times 0.4 = 0.16, \ \alpha_1(3) = \pi_3 b_3(o_1) = 0.4 \times 0.7 = 0.28\]
第二步,递归。时刻2的观测状态是白球,所以时刻2来自盒子1的概率是\[\alpha_2(1) = \Big[\sum\limits_{i=1}^3 \alpha_1(i) a_{i1}\Big] b_2(o_2) = (0.1 \times 0.5 + 0.16 \times 0.3 + 0.28 \times 0.2) \times 0.5 = 0.077\]其他盒子类推,得到\[\alpha_2(2) = 0.1104, \ \alpha_2(3) = 0.0606\] 重复第二步,\[\alpha_3(1) = 0.04187, \ \alpha_3(2) = 0.03551, \ \alpha_3(3) = 0.05284\]
最后我们得到序列的概率\(P(O|\lambda) = \sum\limits_{i=1}^3 \alpha_3(i) = 0.13022\)。
那么后向算法与前向算法类似,但是计算起来相对比较反直觉一点。一样的初始化每个状态最后一个时刻的概率\(\beta_T(i) = 1, i=1, 2, \ldots, N\)。接着根据\(t+1\)时刻的后向概率,递归计算前一个时刻每个隐藏状态的后向概率。也就是\(\beta_t(i) = \sum\limits_{j=1}^N a_{ij}b_j(o_{t+1}) \beta_{t+1}(j), i=1,2,\ldots,N\)。最后\(P(O|\lambda) = \sum\limits_{i=1}^N \pi_i b_i(o_1) \beta_1(i)\)。
一般来说用一个解法来算概率就好了,可以将这两种统一到一个公式上,也就是\(P(O|\lambda) = \sum\limits_{i=1}^N \sum\limits_{i=1}^N \alpha_{t}(i) a_{ij}b_j(o_{t+1}) \beta_{t+1}(j), t=1,2,\ldots,T-1\)。
HMM learning problem
HMM的参数学习有两种一种是有监督学习,一种是无监督学习。
有监督学习比较简单,因为HMM是生成模型,所以有监督学习直接根据标注的隐藏状态计算频率就可以了。也就是\(a_{ij} = \frac{A_{ij}}{\sum_{j=1}^N A_{ij}}, i=1,2,\ldots,N; j=1,2,\ldots,N\),\(b_i(k) = \frac{B_{ik}}{\sum_{k=1}^M B_{ik}}, i=1,2,\ldots,N;\),\(\pi_i = \frac{Count(h_i)}{\sum_{j=1}^N Count(h_j)}\)。
另一种是用EM算法做无监督学习。一般HMM用的是Baum-Welch算法。
EM算法就包括了两个步骤,一个是E,一个是M。我们假设有一个数据集合是\(\{O_1, O_2, \ldots, O_S\}\),\(O_i = o_{i_1}, o_{i_2}, \ldots, o_{i_T}\),\(H_i = h_{i_1}, h_{i_2}, \ldots, h_{i_T}\),为了方便区分,下面用上标来表示隐藏状态的index。\(O=\{o^1, o^2, \ldots, o^M\}\),\(H=\{h^1, h^2, \ldots, h^N\}\)。那么E步就是计算\[Q(\lambda, \bar{\lambda}) = \sum\limits_{H} P(H|O,\bar{\lambda}) \log P(O,H|\bar{\lambda})\] M步就是找到一个\(\bar{\lambda}\)使得上面的期望最大,也就是 \[ \bar{\lambda} = \arg \max_{\lambda} \sum\limits_H P(H|O,\bar{\lambda})\log P(O,H|\lambda) \]
那么\(Q\)函数可以改写成: \[ \sum\limits_{H} P(H|O,\bar{\lambda}) \log P(O,H|\bar{\lambda}) = \sum\limits_{H} \frac{P(H,O|\bar{\lambda})}{P(O|\bar{\lambda})} \log P(O,H|\lambda) \] 因为P(O|{})是常数,所以上面等价于 \[ \sum\limits_{H} P(H,O|\bar{\lambda}) \log P(O,H|\bar{\lambda}) \] 因为\(P(O,H|\lambda) = \pi_{h_1}b_{h_1}(o_1)a_{h_1h_2}b_{h_2}(o_2) \cdots a_{h_{T-1}h_T}b_{h_T}(o_T)\),所以最后将公式可以替换为: \[ Q(\lambda, \bar{\lambda}) = \sum\limits_{H}P(O,H|\bar{\lambda}) \log \pi_{h_1} + \sum\limits_{H}(\sum\limits_{t=1}^{T-1} \log a_{h_t h_{t+1}})P(O,H|\bar{\lambda}) + \sum\limits_{H}(\sum\limits_{t=1}^T \log b_{h_1}(o_t))P(O,H|\bar{\lambda}) \]
那么分步求偏导,我们对第一个部分求偏导, \[ \sum\limits_{H} \log \pi_{h_1} P(O,H| \bar{\lambda}) = \sum\limits_{i=1}^N \log \pi^{i} P(O, h_1 = h^i | \bar{\lambda}) \] 由于\(\sum_{i=1}^N \pi^i = 1\),所以这是受限制的求解极值问题,用拉格朗日乘子法构建拉格朗日函数如下: \[ \sum\limits_{i=1}^N \log \pi^i P(O,h_1 = h^i | \bar{\lambda}) + \gamma(\sum\limits_{i=1}^N \pi^i - 1) \] 接着求导: \[ \frac{\partial}{\partial\pi^i}[\sum\limits_{i=1}^N\log\pi^i P(O,h_1=h^i|\bar{\lambda})+\gamma(\sum\limits_{i=1}^N\pi^i-1)]=P(O,h_1=h^i|\bar{\lambda})+\gamma\pi^i \] 让上式等0,且因为有N个,全部求和就可以得到\(\gamma\)值也就是\(\gamma=-P(O|\bar{\lambda})\)。
所以\(\pi^i = \frac{P(O,h_1 = h^i|\bar{\lambda})}{P(O|\bar{\lambda})}\)。
然后按照一样的方法求第二部分: \[ \sum\limits_{H}(\sum\limits_{t=1}^{T-1}\log a_{h_th_{t+1}})P(O,H|\bar{\lambda})=\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}\log a_{ij}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda}),\sum\limits_{j=1}^N a_{ij}=1 \]
我们设定拉格朗日函数为 \[ L=\sum\limits_{i=1}^N\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}\log a_{ij}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})+\sum\limits_{i=1}^N\gamma_i(\sum\limits_{j=1}^N a_{ij}-1) \]
然后一样求偏导 \[ \frac{\partial L}{\partial a_{ij}}=\sum\limits_{t=1}^{T-1}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})+a_{ij}\sum\limits_{i=1}^N\gamma_i=0 \]
同样通过求和得到\(\sum\limits_{i=1}^N\gamma_i = -\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})\)
最后得到 \[ a_{ij}=\frac{\sum\limits_{t=1}^{T-1}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})}{\sum\limits_{j=1}^N\sum\limits_{t=1}^{T-1}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})}=\frac{\sum\limits_{t=1}^{T-1}P(O,h_t=h^i,h_{t+1}=h^j|\bar{\lambda})}{\sum\limits_{t=1}^{T-1}P(O,h_t=h^i|\bar{\lambda})} \]
现在求最后一部分 \[ \sum\limits_{H}(\sum\limits_{t=1}^{T}\log b_{h_t}(o_t)) P(O,H|\bar{\lambda})=\sum\limits_{i=1}^N \sum\limits_{k=1}^M \sum\limits_{t=1}^T \log b_{ik}P(O,h_t=h^i,o_t=o^k|\bar{\lambda}),\sum\limits_{k=1}^M b_{ik}=1 \]
构造拉格朗日函数 \[ L=\sum\limits_{i=1}^N \sum\limits_{k=1}^M \sum\limits_{t=1}^T \log b_{ik}P(O,h_t=h^i,o_t=o^k|\bar{\lambda})+\sum\limits_{i=1}^N \gamma_i(\sum\limits_{k=1}^Mb_{jk}-1) \]
求偏导 \[ \frac{\partial L}{\partial b_{ik}}=\sum\limits_{t=1}^T P(O,h_t=h^i,o_t=o^k|\bar{\lambda})+b_{ik}\sum\limits_{i=1}^N\gamma_i=0 \]
求和得到\(\sum\limits_{i=1}^N\gamma_i = -\sum\limits_{k=1}^M\sum\limits_{t=1}^T P(O,h_t=h^i,o_t=o^k|\bar{\lambda})\)
最后可以得到 \[ b_{ik}=\frac{\sum\limits_{t=1}^T P(O,h_t=h^i,o_t=o^k|\bar{\lambda})}{\sum\limits_{k=1}^M\sum\limits_{t=1}^T P(O,h_t=h^i,o_t=o^k|\bar{\lambda})}=\frac{\sum\limits_{t=1}^T P(O,h_t=h^i,o_t=o^k|\bar{\lambda})}{\sum\limits_{t=1}^T P(O,h_t=h^i|\bar{\lambda})} \]
按照之前的向前先后算法,计算\(t\)时刻处于隐藏状态\(h^i\)的概率为\(\gamma\),而\(\xi\)表示\(t\)时刻从\(h^i\)转移到\(h^j\)的概率。 \[ P(O,h_t=h^i|\lambda)=\gamma_t(i)=\frac{\alpha_t(i)\beta_t(i)}{\sum_{j=1}^N\alpha_t(j)\beta_t(j)} \]
\[ P(O,h_t=h^i,h_{t+1}=h^j|\lambda)=\xi_t(i,j)=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum\limits_{i=1}^N\sum\limits_{j=1}^N\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)} \]
将上面的两个式子带入之前的偏导结果里面,就得到我们想要的参数了。
HMM decoding problem
最后就是HMM的解码问题,一般来说解码都是用viterbi算法来完成。实践上就是每一步都取最大的可能性,然后记下上一个时刻是哪一个隐藏状态有最大的可能性转移到当前状态。
过程就是
1、\(\delta_1(i) = \pi_i b_i(o_1), i = 1,2,\ldots, N \\ \psi_1(i) = 0, i = 1, 2, \ldots, N\)
2、\(\delta_t(i) = \max\limits_{1 \leqslant j \leqslant N}[\delta_{t-1}(j) \alpha_{ji}] b_i(o_t) \\ \psi_t(i) = \arg \max\limits_{1 \leqslant j \leqslant N}[\delta_{t-1}(j)\alpha_{ji}]\)
3、\(P = \max\limits_{1 \leqslant j \leqslant N} \delta_T(i) \\ i_T = \arg\max\limits_{1 \leqslant j \leqslant N}[\delta_T(i)]\)
CRF
CRF与HMM要解决的问题是类似的,都是要从观测序列中推测出隐藏序列。与HMM不同,CRF是一个典型的有监督学习算法。同样的CRF有一个transition matrix和一个emission matrix。
CRF要优化的loss函数就是一个序列生成的最大概率。 \[ P(y|x) = \frac{1}{Z(x)} \exp \Big(\sum\limits_{i,k} \lambda_k t_k(y_{i-1},y_i, x,i) +\sum\limits_{i,l}\mu_ls_l(y_i, x,i)\Big) \\ Z(x) =\sum\limits_{y} \exp \Big(\sum\limits_{i,k} \lambda_k t_k(y_{i-1},y_i, x,i) +\sum\limits_{i,l}\mu_ls_l(y_i, x,i)\Big) \]
CRF的序列概率计算方式与HMM类似,也是前向-后向算法。这里举一个简单的例子来说明,假设有三个单词,两个隐藏状态。那么emission matrix和transition matrix如下: \[ \begin{array} {|c|c|c|} \hline \ & l_1 & l_2 \\ \hline w_0 & x_{01} & x_{02} \\ \hline w_1 & x_{11} & x_{12} \\ \hline w_2 & x_{21} & x_{22} \\ \hline \end{array} \]
\[ \begin{array} {|c|c|c|} \hline \ & l_1 & l_2 \\ \hline l_1 & t_{11} & t_{12} \\ \hline l_2 & t_{21} & t_{22} \\ \hline \end{array} \]
现在一步一步来前向传播运算序列概率,目标是算出\(log(e^{S_1} + e^{S_2} + \ldots + e^{S_n})\)。
首先第一步,第一个词是\(w_0\),我们有两个变量,\(obs = [x_{01}, x_{02}]\), \(previous = None\),所以\(\text{total_score} = \log(e^{x_{01}} + e^{x_{02}})\)。
第二步从\(w_0 \to w_1\),\(obs = [x_{11}, x_{12}]\),\(previous = [x_{01}, x_{02}]\),接下来为了计算方便,我们对obs和previous做一个broadcast,得到下面的结果: \[ previous = \begin{bmatrix} x_{01} & x_{01} \\ x_{02} & x_{02} \end{bmatrix} \]
\[ obs = \begin{bmatrix} x_{11} & x_{12} \\ x_{11} & x_{12} \end{bmatrix} \]
\[ score = previous + obs + transition = \begin{bmatrix} x_{01} + x_{11} + t_{11} & x_{01} + x_{12} + t_{12} \\ x_{02} + x_{11} + t_{21} & x_{02} + x_{22} + t_{22} \end{bmatrix} \]
然后更新previous,得到 \[previous = [\log(e^{x_{01} + x_{11} + t_{11}} + e^{x_{02} + x_{11} + t_{21}}), \log(e^{x_{01} + x_{12} + t_{12}} + e^{x_{02} + x_{22} + t_{22}})]\]
然后反复迭代得到所有的结果。
这里有个文章里面的图示非常明显:

这样可以完成全部可能路径的概率计算。
接下来就是跟HMM一样的解码问题,同样采用维特比算法就可以解开隐藏序列。如下图: 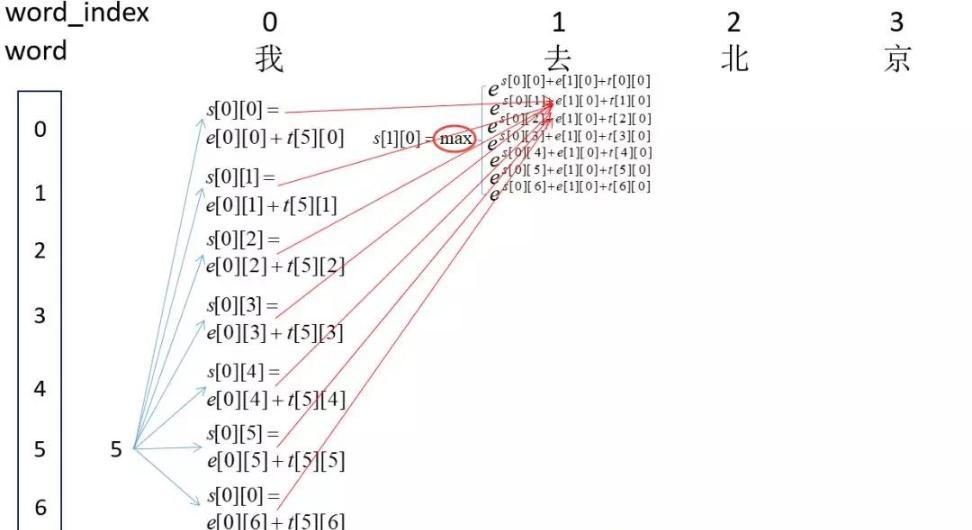
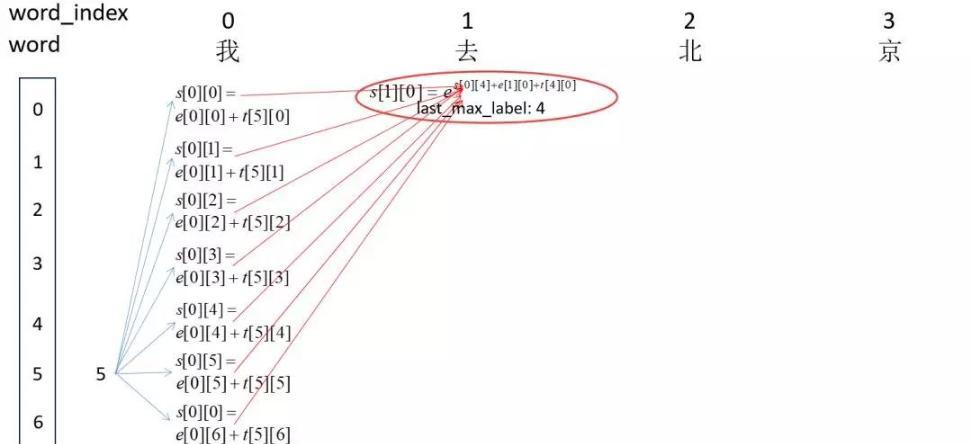


这样就完成了CRF的全过程。至于CRF的参数学习过程,只要用梯度下降去学习那个极大似然函数就可以了。
BiLSTM+CRF
实际上对于命名实体识别任务而言,每一个词后面用BIOES标注,那么是不是直接就可以用LSTM来分类了。实际上也是可以的,用BiLSTM来做如下图:
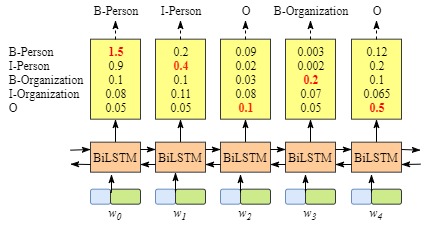
但是纯粹用LSTM来做的话会有一个问题,就是可能输出的分类是不合理的,比如下图:
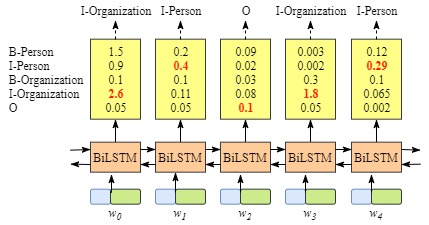
那么这种时候,如果在上层补上CRF的转移矩阵来做限制,就可以得到合理的结果。
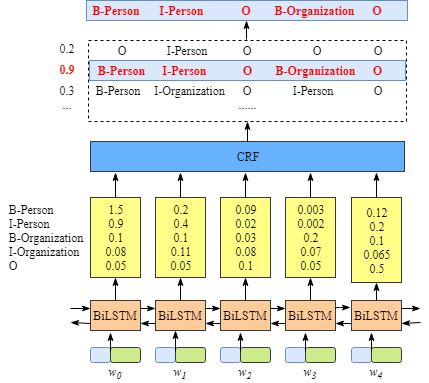
总体而言,我习惯把BiLSTM看做是CRF的改良版,用BiLSTM来替代CRF的emission score学习过程,实现比CRF更好的效果。
具体的代码可以直接看PyTorch的官方教程,不过里面的是单个记录的训练,大规模训练比较慢,我这里改了一版基于batch训练的可以参考。notebook地址。
