深度学习调参技巧入门
深度学习有很多框架,个人最喜欢的是dmlc的MXNet还有PyTorch。keras是另外一个非常友好的框架,后台可以调用tensorflow,但是tensorflow本身不是一个非常友好的框架,所以有兴趣的可以自己看看,上手很快。
这里大概介绍深度学习炼丹的一些入门技巧。
之前提到,深度学习也是机器学习的一个特例,因此深度学习的过程也是设计模型,计算模型的好坏,选择一个最好的模型。
最基础的一个方法跟一般机器学习一样,先看在training上的效果,如果够好,再看在testing上的效果。但是这里有个不同,一般的机器学习基本上都可以在training上得到百分百正确的结果,例如决策树。但是深度学习并不一定能够在training上得到百分百正确。因此在训练深度学习的时候,不要一步到位只看testing的效果。
这里有入门的五个小技巧:
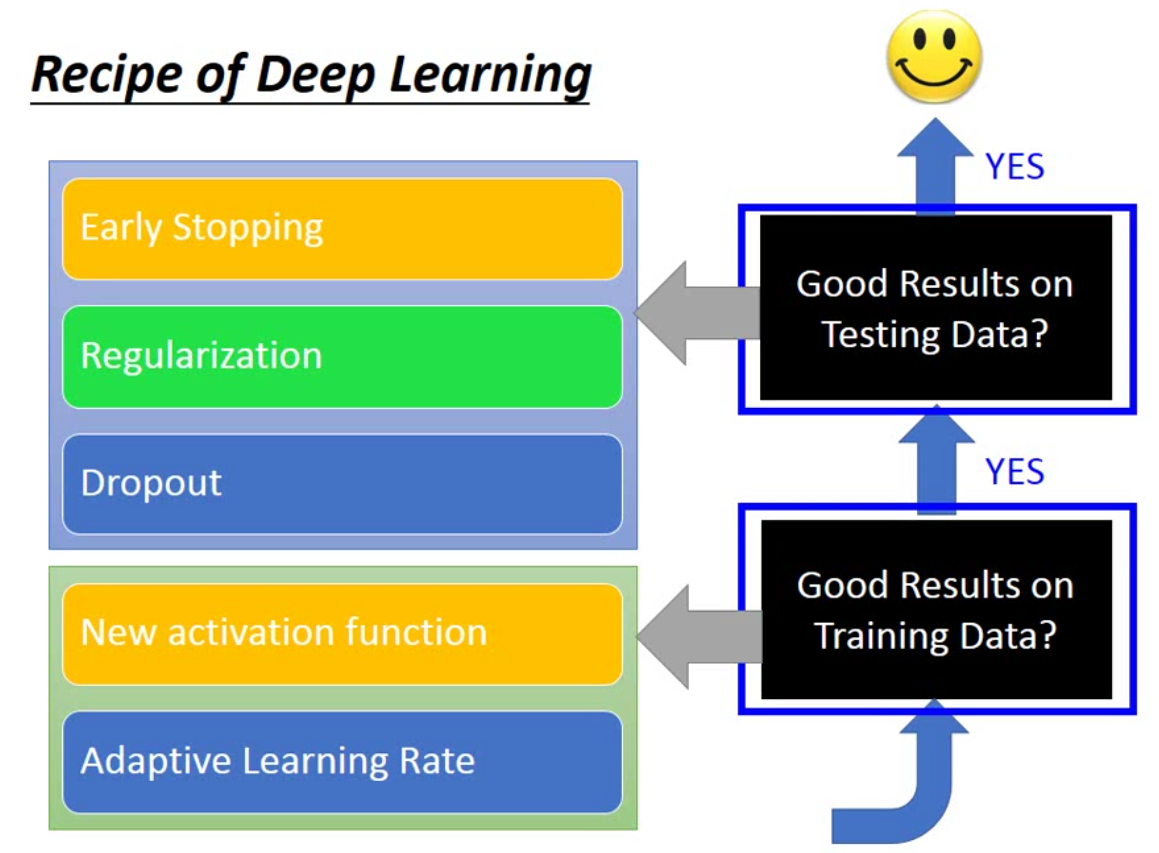
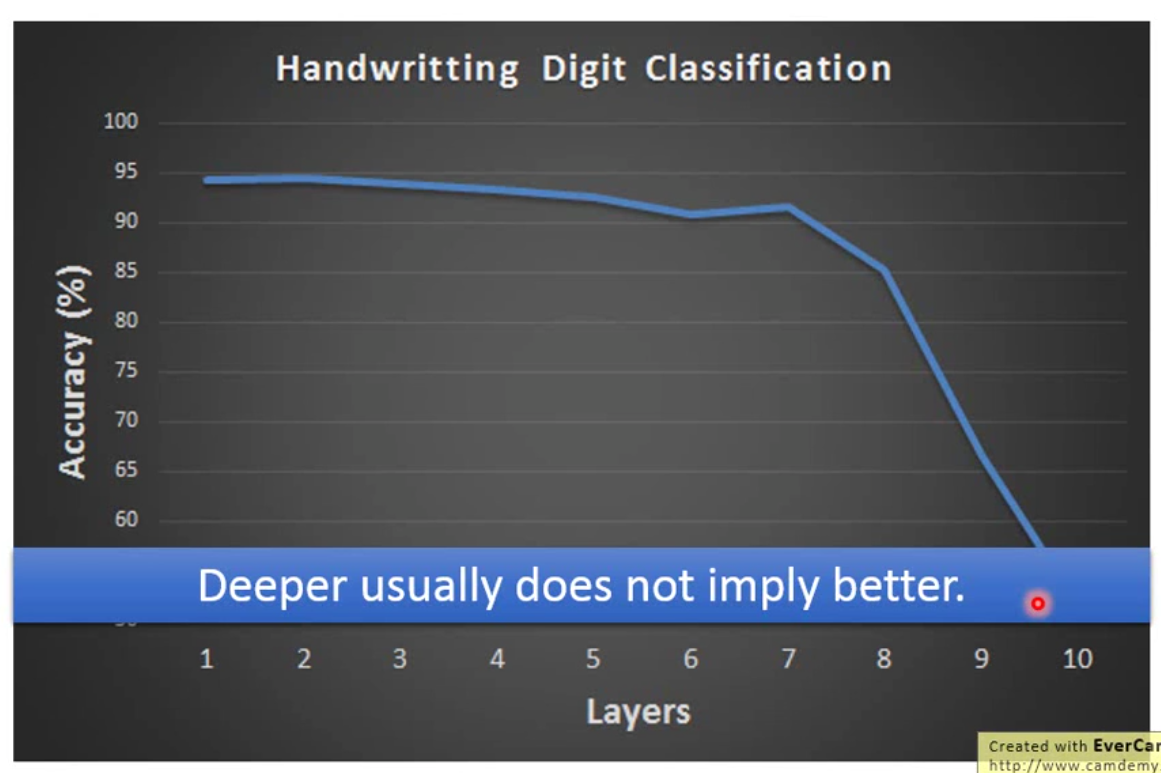
那么首先我们想一下,是否深度网络越深效果越好呢?答案是不一定的。举例而言,用全连接层和sigmoid函数训练mnist的时候,当层数加到很大的时候,训练效果可能就很不好了。
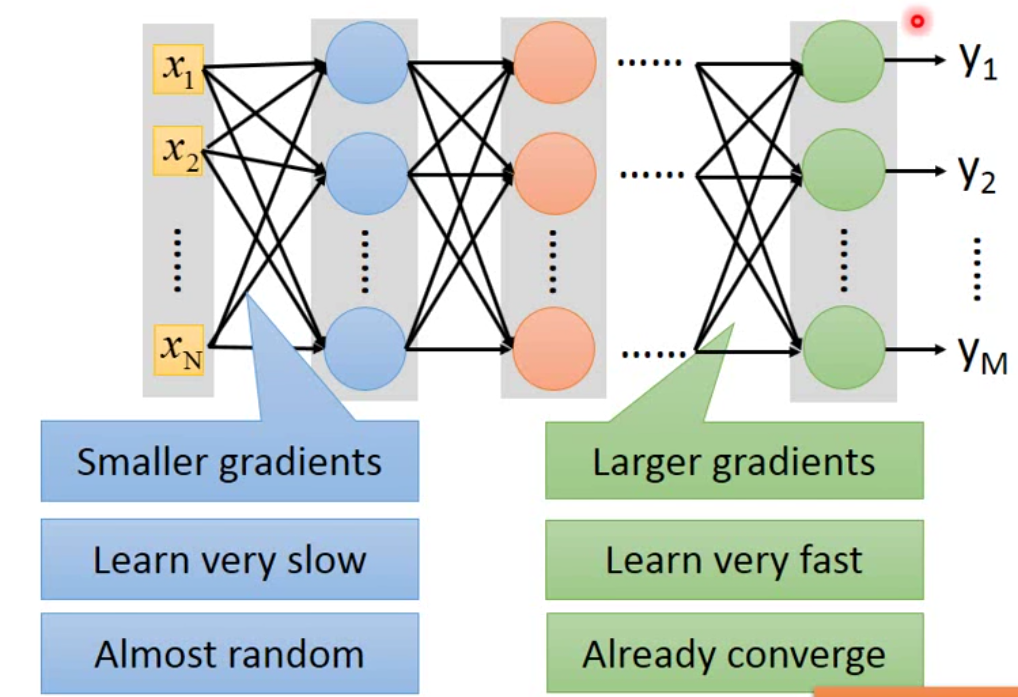
一般而言,如果我们的neuron用的是sigmoid函数,那么我们会发生这样的现象。这个现象的原因就是梯度消失 Vanishing Gradient。
所以,按照之前的反向传播更新参数的方法,靠近output layer的地方参数已经更新完毕,但是靠近input layer的地方还没train。用图形表示如下:
那sigmoid函数为什么会发生这样的事情呢?我们不用严格去计算\(\frac{\partial l}{\partial w}\),按照导数的定义,我们可以知道,\(\frac{\partial l}{\partial w} = \frac{\Delta l}{\Delta w}\)。所以我们把这种思想代入sigmoid作为激活函数的神经网络当中,我们可以发现当第一层的\(w_1\)发生很大的变化,那么\(z_1 = w_1 \cdot x + b_1\)发生很大的变化,但是经过sigmoid函数后,这个变化被缩小了,因此\(\sigma(z_1)\)是小于\(z_1\)的,而随着层数的增加,这样的影响就会不断加强。这就导致了在input layer地方的梯度会变得很小。也就是梯度消失的问题。
那么理论上而言,用dynamic的learning rate也是可以解决这样的问题的,但是直接将sigmoid函数替换掉来得更干脆一点。
现在有一个很常用的激活函数是ReLu(Recitified Linear Unit)。ReLu有很多好处,一个是求导更快;一个是Hinton提出无数个sigmoid叠加可以得到ReLu;当然,最重要的是ReLu可以解决梯度消失的问题。ReLu的函数可以表示如下: \[ a = \begin{cases} 0, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \] 这样的一个激活函数不是一个连续可导的函数,那么梯度下降是依赖于导数的,能不能求解呢?
事实上,因为ReLu是分段可导的,而且在实际模型中,经过ReLu计算的神经元,每一层会有有一半的神经元是0,因此,如果现在一个神经网络的激活函数用的是ReLU,那么我们可以将整个神经网络表示为:
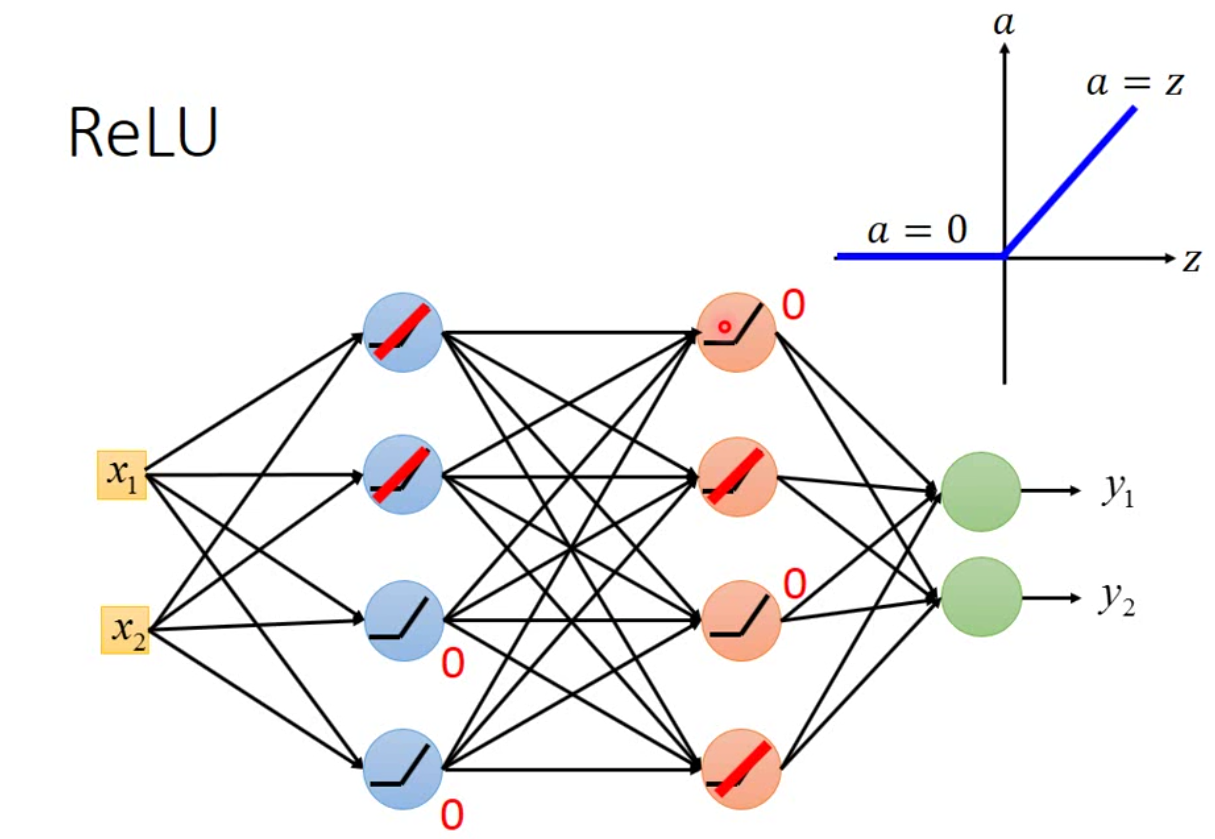
那我们可以将那些\(0\)的neuron直接不要掉,得到一个更瘦的网络。那因为现在的网络变成了线性的神经元,因此每次传递的梯度没有经过缩放,因此不会有梯度消失的问题。
ReLu有各种各样的变型,一种是Leaky ReLu: \[ a = \begin{cases} 0.01z, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \] 还有一个种是parametric ReLu: \[ a = \begin{cases} \alpha z, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \]
那事实上我们可以让网络自己决定每个neuron要用什么样的激活函数。这样的结构是Goodfellow提出的maxout network。maxout network跟之前的网络不一样的地方是,原先下图中我们得到的\(5\),\(7\)这些数字都是要经过activation function变成其他值的。但是在maxout network里面,我们会把这些值变成一个group,然后去group里面的比较大的一个值作为output。这个事情,其实跟CNN里面的max pooling一样。
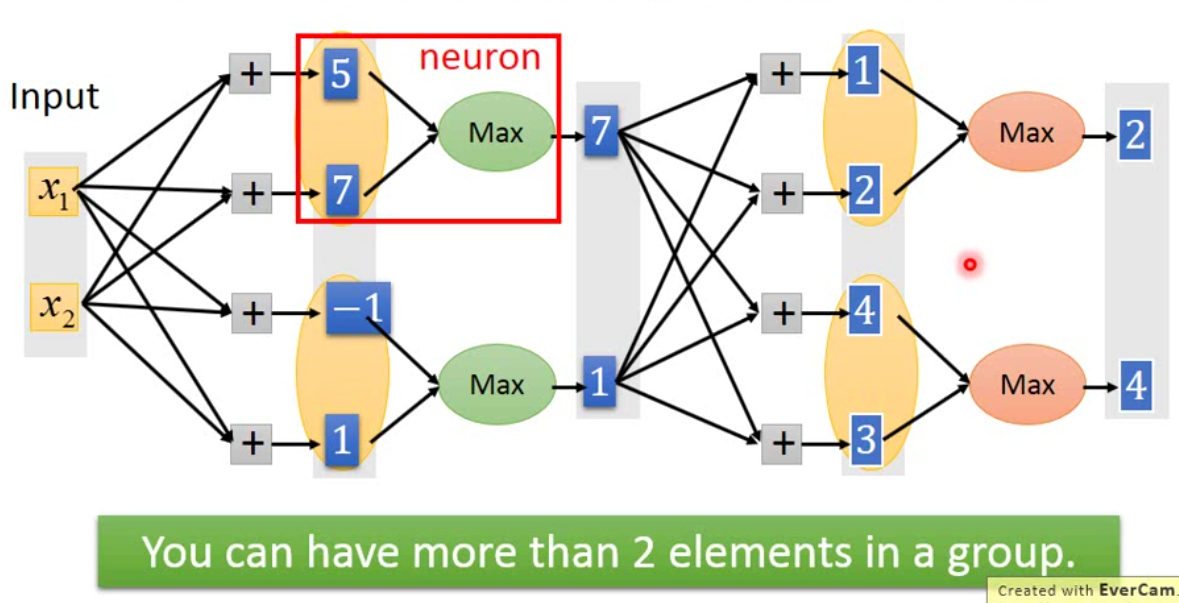
这个网络中,哪几个神经元要结合,每个group中放多少个element需要事先设定好。由此我们可以发现,ReLu其实是maxout的一种特殊情况,而ReLu的其他变种也是,都是maxout的真子集。那事实上maxout并不能学习非线性的activation function,它只能学习分段线性的激活函数。
那我们如果element放的越多,maxout network学到的激活函数分段就越多。从某种程度上而言,maxout network比较强的地方就是,不同的样本喂进去以后,通过更新\(w\),可能得到ReLu,也可能得到Leaky ReLu这样的activation function,也可能是其他的activation function。也就是说maxout network是一个会学习的网络。
现在的问题是,这样一个分段的函数是否开进行梯度下降呢?实践上而言,这是可行的。因为在maxout network中,每一次传递的都是最大的那个值,那其余的神经元不对loss做贡献,因此每一次传递的都是一个linear的结果,那梯度下降是可以对linear的函数求解的。这里不用担心有一些\(w\)不会被训练到,因为不同的batch喂进去的时候,不同的\(w\)会被影响到。示意图如下:
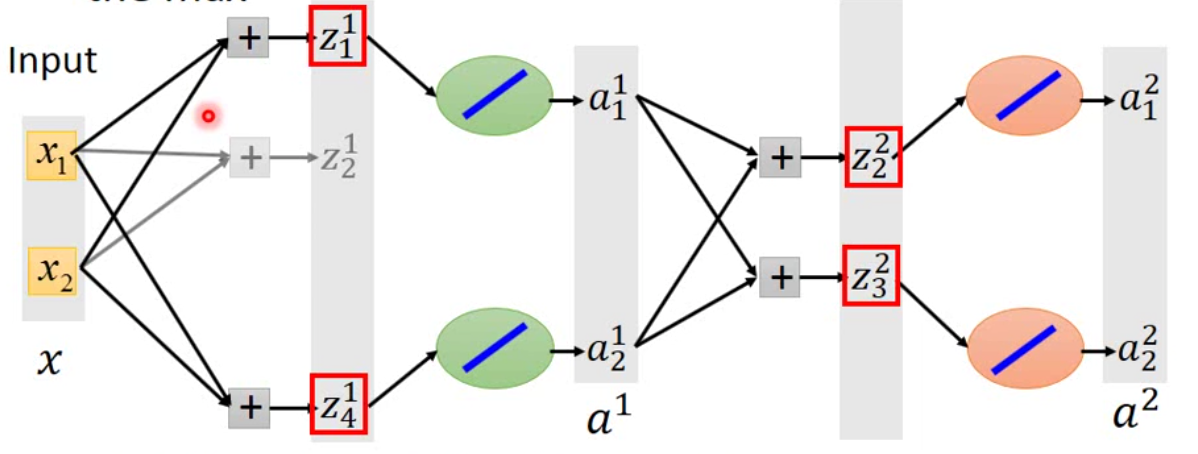
在这个网络中,\(z_2^1\)没被训练到,但是如果用一笔新的数据,就有可能训练到这个值。
另外如果不调整激活函数,我们就可以使用adagrad这样的方法。现在回顾一下adagrad,adagrad更新参数的方法是: \[ w^{t+1} = w^t - \frac{\eta}{\sqrt{\sum g_i^2}} g^t \]
Hinton 提出了一种新的更新方法,RMSProp,更新步骤如下: \[ w^{t+1} = w^t - \frac{\eta}{\sigma^t} g^t, \sigma^t = \sqrt{\alpha (\sigma^{t-1})^2 + (1-\alpha) (g^t)^2} \] 这是对Adagrad的一种变形。
此外,我们也可以用物理的方法来考虑一下梯度下降。在物理世界中,一个小球从山丘向下滚动的时候,会因为惯性的关系继续滚动下去,越过saddle point,甚至可能越过一些小坑和小坡。因此我们也可以在梯度下降中加入一个类似的概念。示意如下:
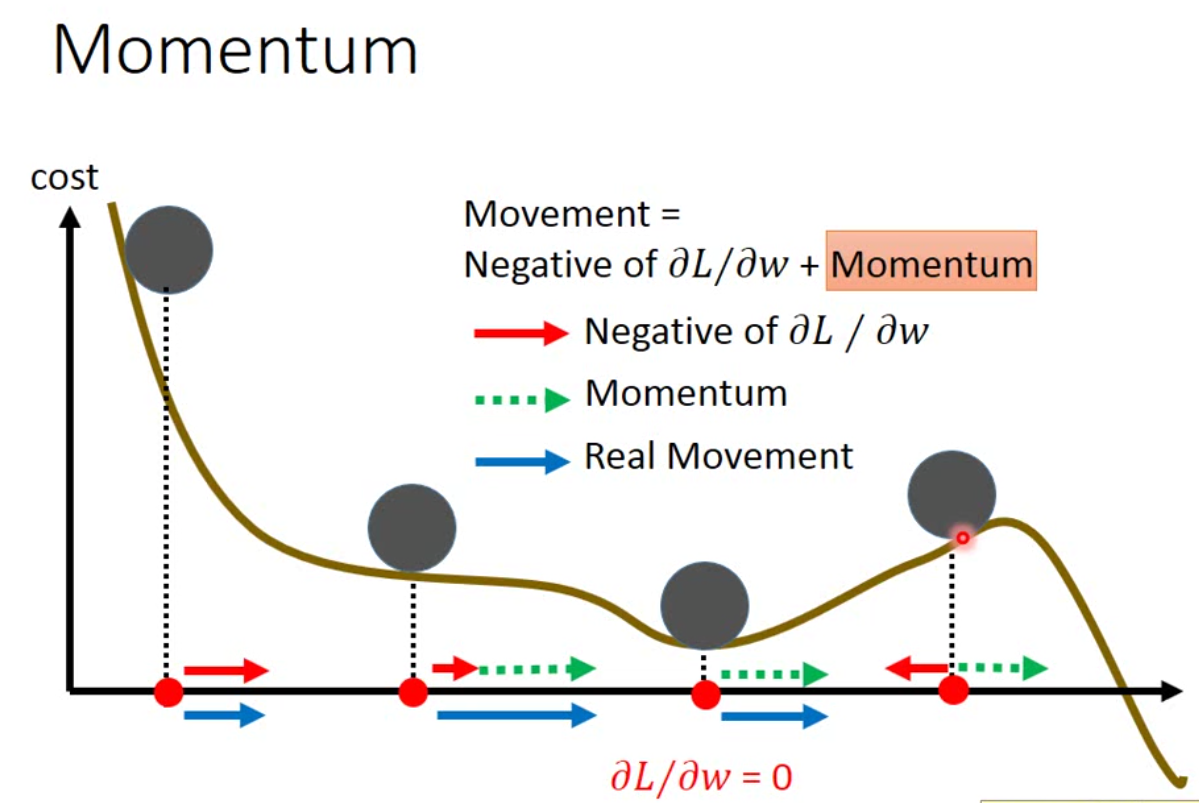
一般而言,这样的方法能躲过saddle point,但是不一定能够躲过local minimum。现在如果我们考虑了monentum,那么我们的迭代方式就是: \[ w^{t+1} = w^t + v^{t+1} \\ v^{t+1} = \lambda v^t - \eta g^{t+1} \] 我们可以看到,实际上用momentum的更新方法,我们实际上是考虑了之前每一次的移动。现在流行的Adam这个方法,实际上结合了RMSProp和momentum两种。
那上面两种方法都是针对training进行优化的。现在看另外三种对testing进行优化的方法。
第一种是early stopping。 Early stopping就是当模型在validation set上没有提升的情况下,就提前停止模型训练。当然,前提是模型在training上面可以正常收敛。
第二种是regularization。Regularization有两种,一种是L1 regularization,另一种是L2 regularization。
L2 regularization表示如下: \[ L'(\theta) = L(\theta) + \lambda \frac{1}{2}||\theta||_2, \quad ||\theta||_2 = (w_1)^2 + (w_2)^2 + \dots + (w_n)^2 \] 那么我们更新参数的方法就是: \[ w^{t+1} = w^t - \eta \frac{\partial L'}{\partial w} = w^t - \eta (\frac{\partial L}{\partial w} + \lambda w^t) = (1-\eta \lambda)w^t - \eta \frac{\partial L}{\partial w} \] 由于后面还跟了一个当前的梯度,因此不用担心这样的更新方法会导致所有的参数迭代到0。
那L1 regularization表示如下: \[ L'(\theta) = L(\theta) + \lambda ||\theta||_1, \quad ||\theta||_1 = |w_1| + |w_2| + \dots + |w_n| \] 所以我们更新参数的方法就是: \[ w^{t+1} = w^{t} - \eta \frac{\partial L'}{\partial w} = w^t - \eta(\frac{\partial L}{\partial w} + \lambda \text{sign}(w^t)) \] 所以用L1,我们的参数每一次都会向0移动一个\(\lambda \eta\)。
实际上因为deep learning在初始化参数的时候,都会选择接近0的位置开始,因此实际上regularization在深度学习当中的作用可能还不如early stopping来得有用。
最后一种就是dropout。dropout就是随机丢掉一部分的neuron,每一次mini-batch进入网络,都要重新dropout一些网络,也就是每一个batch的网络实际上是不一样的。从某种程度而言,这也是一种集成算法。
这里需要注意的是,我们在training的时候需要进行dropout,但是在testing的时候是不进行dropout的。那这个时候,我们在training学到的\(w\),在testing上就要将\(w\)乘以\(1-p\),其中\(p\)是dropout的概率。
那为什么要做这样的动作呢?之前我们说过,dropout是也是一种ensemble,ensemble方法如下:
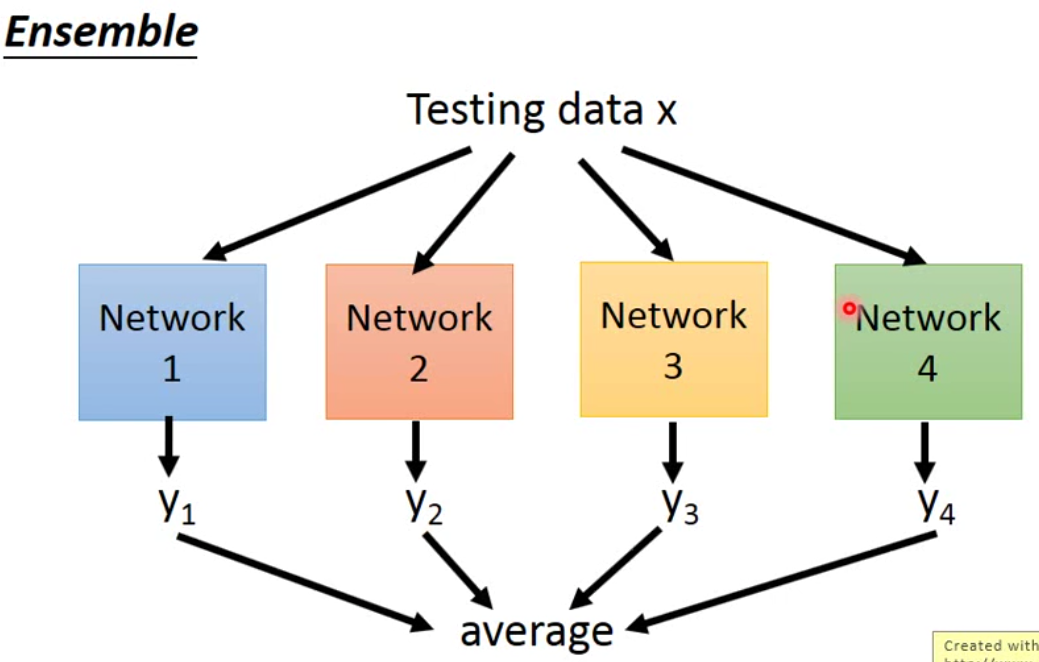
那dropout实际上是ensemble的一个变种。因为每一个neuron都有可能被drop,假设有m个neuron,那么我们理论上有可能得到\(2^m\)种网络,而这些网络之间有些参数是共用的。
那如果我们用ensemble的方法,那么我们就是将所有网络的结果进行平均。但是dropout是直接将所有的参数乘以\(1-p\),然后直接预测。而神奇的地方就在于,这样的方法得到结果跟ensemble的结果是接近的。
举例而言,如下图:
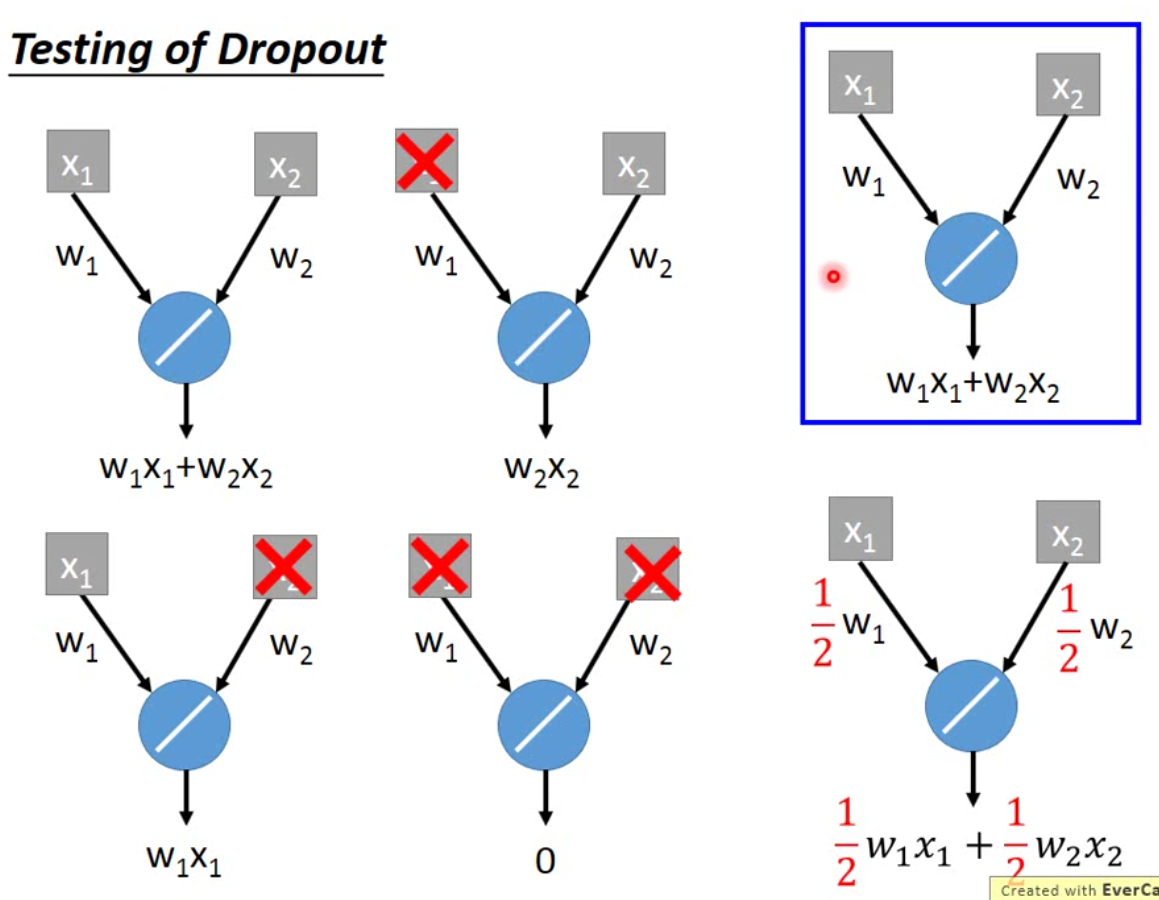
我们假设右上角就是我们用dropout训练好的模型,那么这个模型所有可能出现的network是左边的四种。假设每个neuron被dropout的概率一样,都是0.5,那么这四种结构出现的概率就是一样的,因此这四个结构的average就是右下角的结果,刚好就是training的weight乘以\(1-p\)。
那实际上,这个事情理论上只有在activation function是linear的时候才能work,nonlinear的模型实际上是不work的。但是神奇的就是,在真实使用的时候,nonlinear的模型,一样也可以使用。不过一般来说,如果activation function是linear的时候,dropout的效果会比较好。
以上就是深度学习入门级的调参技巧。还是散沙的一句话,深度学习已经变成实验科学了,多动手是王道。
