分类算法常年扛把子,逻辑回归
逻辑回归是按照线性的方程进行分类的算法。最基本的逻辑回归是针对二分类的。二分类的数据我们记取值范围为\([0, 1]\),由于回归方程不能直接对分类数据进行计算,因此我们引入\(\sigma\)函数。 \[
\sigma(z) = \frac{1}{1+\exp(-z)}.
\] \(\sigma\)函数的作用就是将二分类的值平滑成一条曲线。 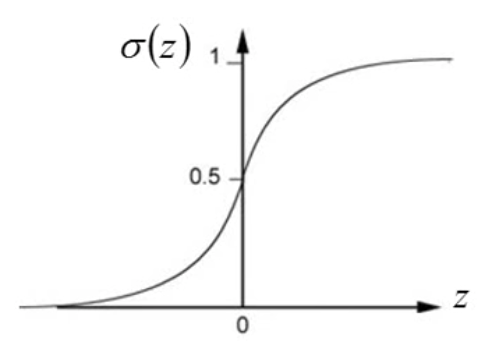
在开始逻辑回归之前,先回顾一下上一篇博客的内容。上一篇大致介绍了贝叶斯方法。贝叶斯方法是按照 posterior probability 来进行分类的。
posterior probability 在二分类时候表示为: \[ \begin{align} \text{P}(C_1|x) &= \frac{\text{P}(x|C_1) \text{P}(C_1)}{\text{P}(x|C_1) \text{P}(C_1) + \text{P}(x|C_2) \text{P}(C_2)} \\ &= \frac{1}{1+\frac{\text{P}(x|C_2) \text{P}(C_2)}{\text{P}(x|C_1) \text{P}(C_1)}} \\ &= \frac{1}{1+\exp(-z)} \\ &= \sigma(z) \end{align} \]
我们很神奇地发现,其实上下都除以分子以后,就变成了sigmoid函数的样子。
因此,\(z = -\ln(\frac{\text{P}(x|C_2) \text{P}(C_2)}{\text{P}(x|C_1) \text{P}(C_1)}) = \ln(\frac{\text{P}(x|C_1) \text{P}(C_1)}{\text{P}(x|C_2) \text{P}(C_2)})\)。之前假设数据分布是符合正态分布的,因此\(\text{P}(x|C_i) \text{P}(C_i)\)符合正态分布\(\frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma|^{1/2}} \exp(-\frac{1}{2}(x-\mu)^{\top} \Sigma^{-1} (x-\mu))\)。 因为\(P(C_i) = \frac{N_i}{\sum N_n}\),因此\(z = \ln(\frac{\text{P}(C_1)}{\text{P}(C_2)}) + \ln(\frac{\frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma_1|^{1/2}} \exp(-\frac{1}{2}(x-\mu_1)^{\top} \Sigma_1^{-1} (x-\mu_1))}{\frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma_2|^{1/2}} \exp(-\frac{1}{2}(x-\mu_2)^{\top} \Sigma_2^{-1} (x-\mu_2))})\)。加号左边就是一个常数,很好计算,先不去管,化简一下右边的部分。 \[ \ln(\frac{\frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma_1|^{1/2}} \exp(-\frac{1}{2}(x-\mu_1)^{\top} \Sigma_1^{-1} (x-\mu_1))}{\frac{1}{(2\pi)^{D/2}} \frac{1}{|\Sigma_2|^{1/2}} \exp(-\frac{1}{2}(x-\mu_2)^{\top} \Sigma_2^{-1} (x-\mu_2))}) = \ln(\frac{\frac{1}{|\Sigma_1|^{1/2}}}{\frac{1}{|\Sigma_2|^{1/2}}}) + \ln(\frac{\exp(-\frac{1}{2}(x-\mu_1)^{\top} \Sigma_1^{-1} (x-\mu_1))}{\exp(-\frac{1}{2}(x-\mu_2)^{\top} \Sigma_2^{-1} (x-\mu_2))}) \] 因为我们在上一节课中假设了两个变量的方差相等,因此上面式子的左边部分又可以消掉,只剩下右边部分。 将右边部分展开化简: \[ \begin{align} \ln(\frac{\exp(-\frac{1}{2}(x-\mu_1)^{\top} \Sigma_1^{-1} (x-\mu_1))}{\exp(-\frac{1}{2}(x-\mu_2)^{\top} \Sigma_2^{-1} (x-\mu_2))}) &= \ln(\exp(-\frac{1}{2}(x-\mu_1)^{\top} \Sigma_1^{-1} (x-\mu_1))) - \ln(\exp(-\frac{1}{2}(x-\mu_2)^{\top} \Sigma_2^{-1} (x-\mu_2))) \\ &=-\frac{1}{2}\Big[(x-\mu_1)^{\top}\Sigma^{-1}_1(x-\mu_1) - (x-\mu_2)^{\top}\Sigma^{-1}_2(x-\mu_2) \Big] \\ &= -\frac{1}{2}\Big[x^{\top} \Sigma^{-1}_1 x - x^{\top} \Sigma^{-1}_1 \mu_1 - \mu_1^{\top} \Sigma_1^{-1} x + \mu_1^{\top} \Sigma_1^{-1} \mu_1 - (x^{\top} \Sigma^{-1}_2 x - x^{\top} \Sigma^{-1}_2 \mu_2 - \mu_2^{\top} \Sigma_2^{-1} x + \mu_2^{\top} \Sigma_2^{-1} \mu_2) \Big] \\ &= -\frac{1}{2} \Big[ -2(x^{\top}\Sigma^{-1}\mu_1 - x^{\top}\Sigma^{-1}\mu_2) + \mu_1^{\top} \Sigma^{-1} \mu_1 - \mu_2^{\top} \Sigma^{-1} \mu_2 \Big] \end{align} \] 将这个结果代回原来的式子当中,我们可以得到,其实这也是一个线性模型。 \[ z = (\mu_1 - \mu_2)^{\top} \Sigma^{-1} x - \frac{1}{2}(\mu_1)^{\top}(\Sigma)^{-1} \mu_1 + \frac{1}{2}(\mu_2)^{\top}(\Sigma)^{-1} \mu_2 + \ln(\frac{N_1}{N_2}) \] 所以,\(\boldsymbol{w}^{\top} = (\mu_1 - \mu_2)^{\top} \Sigma^{-1},b = \frac{1}{2}(\mu_1)^{\top}(\Sigma)^{-1} \mu_1 + \frac{1}{2}(\mu_2)^{\top}(\Sigma)^{-1} \mu_2 + \ln(\frac{N_1}{N_2})\)。
这个式子看起来很复杂,但是其实化简之后就是之前的线性模型。那么上一节课中,我们用的方法是 generate probability 的方法,也就是我们根据数据的情况,假设数据符合某种分布,比较常用的是正态分布,根据数据的均值和协方差矩阵计算当我们 sample 到一个 point 的时候,那么它属于某个 \(\text{class}_i\) 的概率是多少。
这种方法也叫作线性判别,也就是 LDA ,需要跟 NLP 中的 LDA 区别。如果我们假设每个变量之间都是完全独立的,那么这个模型就变成了朴素贝叶斯模型。想想就觉得好神奇诶 :-)。
现在问题来了,如果是一个线性模型,那么我们能不能用梯度下降的方法一次性把参数学出来,而不是去计算好几个均值和方差?
首先我们先按照最早的线性模型的方法,构造我们的 function set。逻辑回归的目的是为了计算一个 sample 属于某个类别的概率有多少,因此,我们构建的函数可以是: \[ f_{w, b}(x) = P_{w, b}(C_1|x) = \sigma(z) \] 其中\(z = w \cdot x + b = \sum w_i x_i + b\),这样就可以包括所有可能的\(w,b\)。
同回归模型相比,因为逻辑回归这里加入了 sigmoid 函数,因此逻辑回归的取值范围只有\((0, 1)\),而线性方程因为没有做任何限制,因此取值是\((-\infty, \infty)\)。
现在我们有了模型,那么如何衡量模型的好坏呢?参考原来的极大似然法,我们可以得到: \[ L(w, b) = f_{w, b}(x^1)f_{w, b}(x^2)(1-f_{w, b}(x^3)) \dots \] 我们的目的是让这个概率最大,也就是 \[ w^*, b^* = \arg \max_{w,b}(L(w, b)) = \arg \min_{w, b}-\ln(L(w, b)) \] 我们假设 class 1 是 1, class 2 是 0。那么我们的目标函数就能写作: \[ \sum_n-\Big[y^n \ln f_{w, b}(x^n) + (1-y^n) \ln (1-f_{w, b}(x^n)) \Big] \] 这个其实就是信息论里的交叉熵。交叉熵定义为:\(H(p, q) = - \sum_x p(x) \ln(q(x))\)。因此,在这里,我们的 loss function 就可以定义为 \(L(f) = \sum_n C(f(x^n), y^n)\)。根据交叉熵的意义,当\(f(x^n)\)与真实概率越接近,交叉熵越小。
得到这个损失函数,我们就可以用梯度下降的方法来求解。我们想让损失函数最小,可以对其求偏导。实际上就是对 \(\ln f_{w,b}(x^n)\) 和 \(\ln (1-f_{w,b}(x^n))\) 求偏导。
分别计算一下,第一个式子: \[ \begin{align} \frac{\partial{\ln(f(x^n))}}{\partial{w_i}} &= \frac{\partial{\ln \sigma(z)}}{\partial{z}} \frac{\partial{z}}{\partial{w_i}} \\ &= \frac{\partial{\sigma(z)}}{\sigma(z)} \frac{\partial{\sigma(z)}}{\partial{z}} \frac{\partial{z}}{\partial{w_i}} \\ &= \frac{1}{\sigma} \sigma(1-\sigma) x^n \\ &= (1-\sigma)x^n \end{align} \] 第二个式子: \[ \begin{align} \frac{\partial \ln(1-f_{w,b}(x))}{\partial w_i} &= -\frac{1}{1-\sigma} \sigma(1-\sigma) x \\ &= -\sigma x \end{align} \] 代回原来的公式中,我们就能得到,原来函数对 \(w_i\) 的偏导数为: \[ \sum_n -\Big[y^n(1-\sigma)x^n_i - (1-y^n)\sigma x_i^n \Big] = \sum_n -\Big[y^n - y^n \sigma - \sigma + y^n \sigma \Big] x_i^n = \sum_n -(y^n - \sigma)x^n_i \]
那么我们发现一个很有意思的事情,那就是,这个梯度下降的方程,和我们最早的 linear regression 的梯度下降是一模一样的。
这里就有一个问题,为什么同样是线性模型,这里不可以使用回归模型中的 MSE 作为 loss function?
我们这里强行使用 MSE 试验一下。
如果今天的 loss function 是 MSE,那么,我们的偏导数就是: \[ \begin{align} \frac{\partial \frac{1}{2}(f_{w, b}(x) - y)^2 }{\partial w_i} &= (f_{w, b}(x) - y) \frac{\partial f_{w, b}(x)}{\partial z} \frac{\partial z}{\partial w_i} \\ &= (f_{w, b}(x) - y) f_{w, b}(x) (1 - f_{w, b}(x)) x_i \end{align} \] 假如,我们的\(y=1\),如果\(f_{w, b}(x) = 1\),那么我们的偏导数趋近于0,非常好。但是如果现在我们的\(f_{w, b}(x) = 0\),我们会发现,其实我们的损失函数依然等于0。 同样的,如果\(y=0\)也会得到这样的结果。
下图就是这个结果的原因:
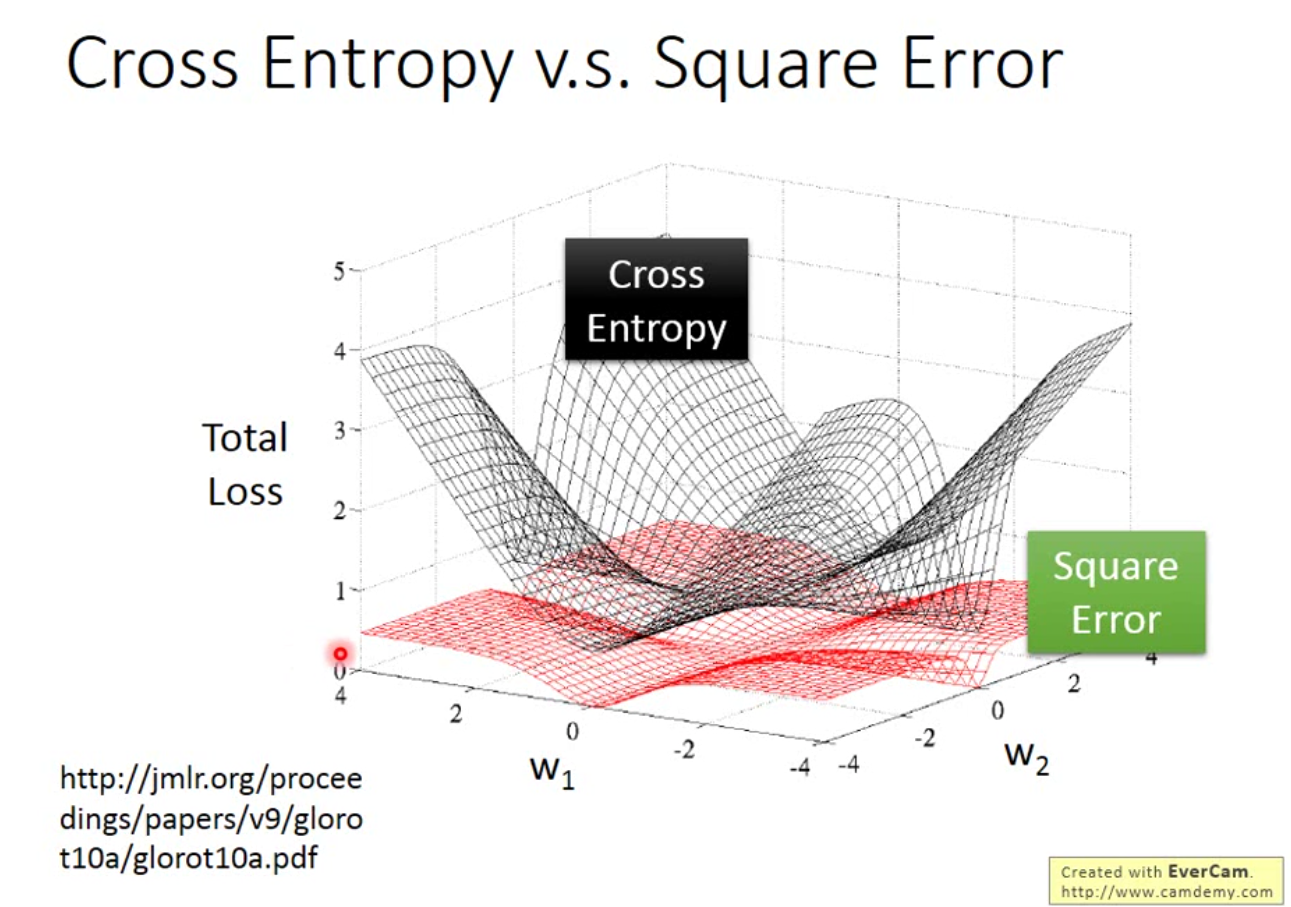
一般情况下,逻辑回归这类的模型称为 Discriminative ,而上一节里的LDA,或者贝叶斯方法被称为 Generative。
一般情况下,Discriminative model 会比 Generative model 要好。但是因为 Generative model 带入了一定的分布的假设,因此只需要少量的数据就可以训练,同时对噪音比较鲁棒。另外,先验分布和类别依赖可以从不同的数据来源进行估计。
对于多分类问题,与二分类类似,我们对每一个类别计算\(\sigma\)函数,计算\(y_i = \frac{e^{z_i}}{\sum e^(z_j)}\),这个就叫做 Softmax。那么\(y_i\)就可以看成是属于 class i 的概率。然后依然用 cross entropy 作为 loss function,就能得到我们想要的结果。
那么事实上逻辑回归有很明显的缺点,那就是逻辑回归无法解决 XOR 问题。如何解决 XOR 问题呢?最简单的方法是做坐标映射,将原线性不可分的坐标映射到线性可分的空间中。但是事实上,这种坐标映射是非常 tricky 的,一般有 domain knowledge 会有很大的帮助,但是如果什么都不会怎么办呢? 我们就可以使用两个逻辑回归来将原来的坐标进行转换。示例图如下:
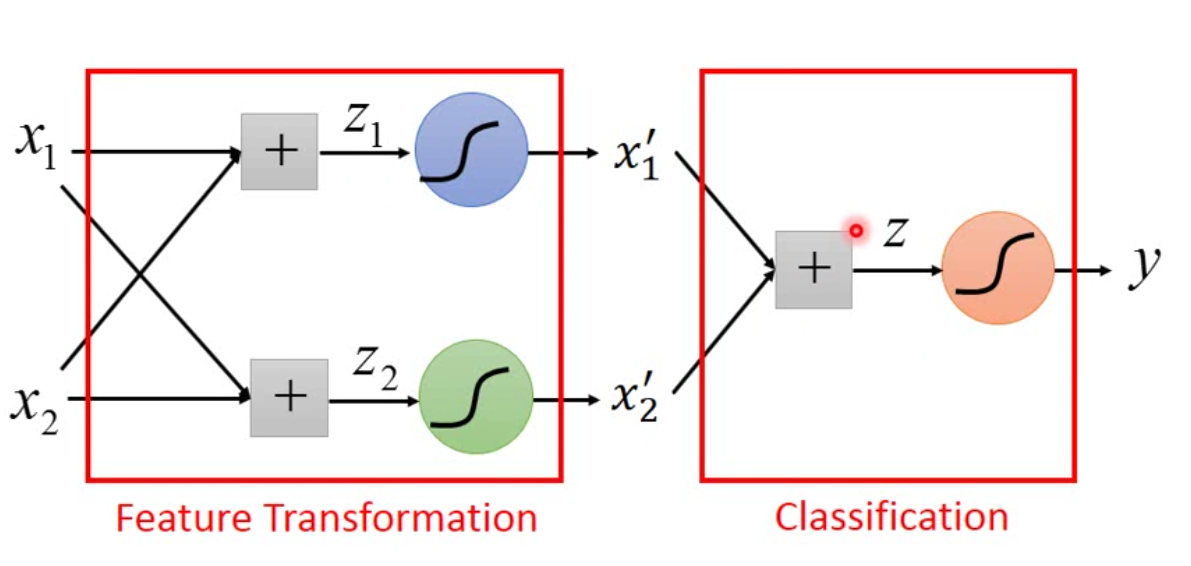
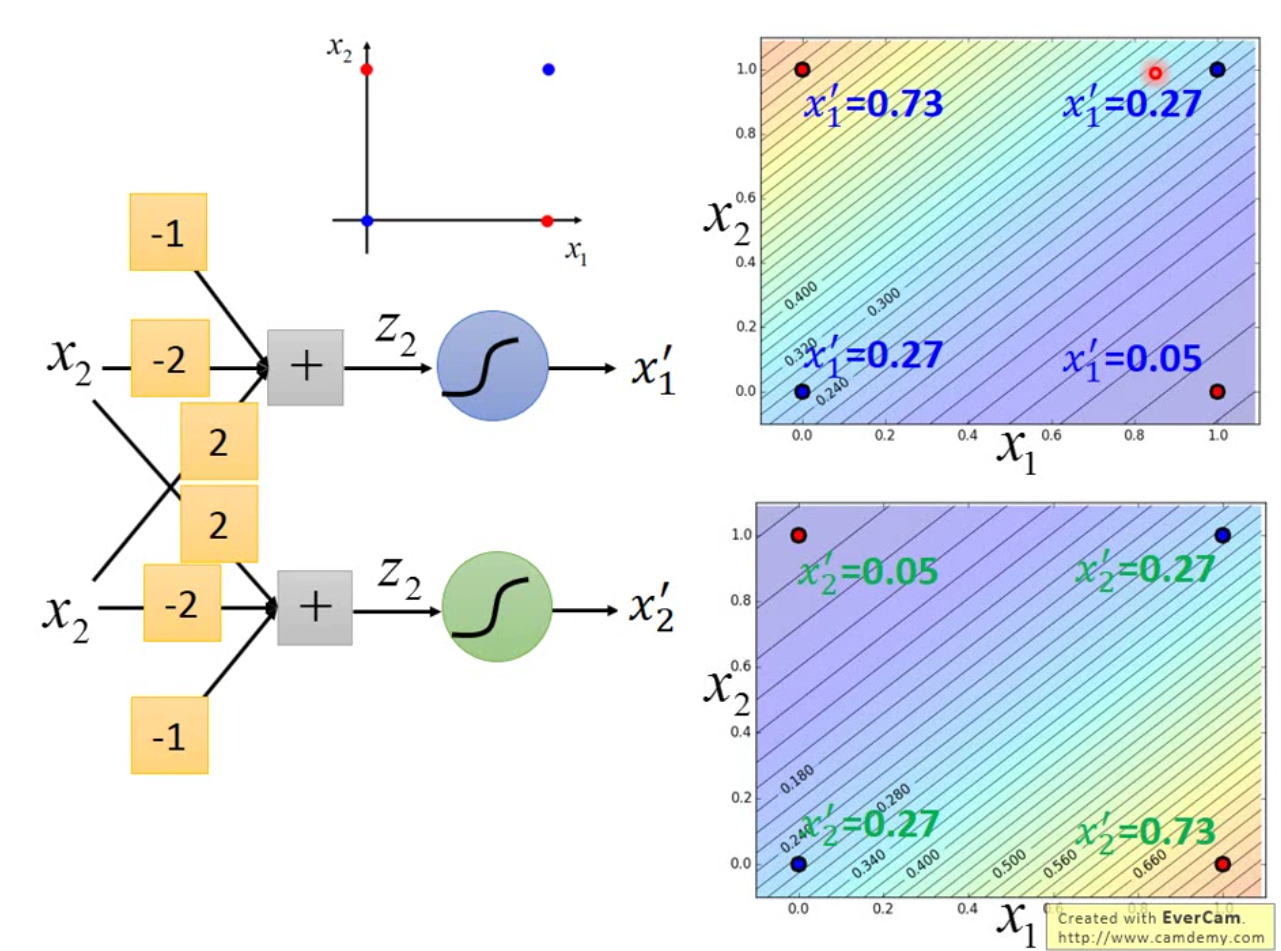
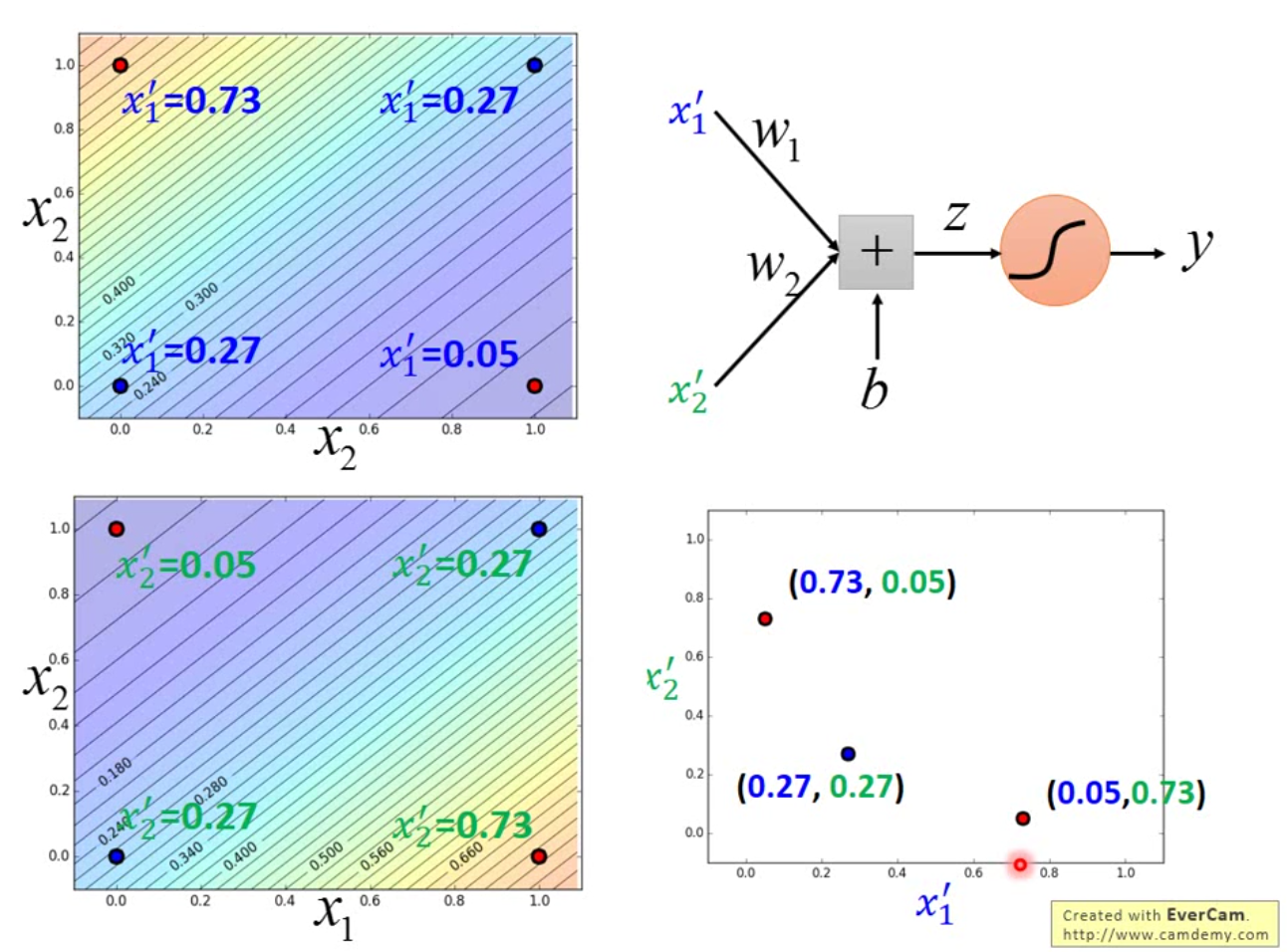
我们构造这样的一个模型,先用两个逻辑回归进行 feature transform,再用一个逻辑回归进行分类。
这样的设计就是传说中的多层感知机(MLP),也就是传统的神经网络,我们将这中间的每一个模型叫做神经元,每一个平行的神经元之间就叫做层。多放几层就变成了现在最火的深度学习,再加宽一点,也就是多放一些神经元,就能硬刚各种模型了。好神奇诶。
那么一个逻辑回归可以梯度下降,这里有三个,怎么算呢?现在的框架下,这三个模型是可以同时学习参数的。下一节的内容就是关于深度学习的。
