分类算法的一些提纲挈领的概念。
分类算法就是将数据喂给模型,模型输出这一笔数据属于哪一类。而之前的回归算法是喂一部分数据后吐出一串连续值。
不同于回归,分类模型的 Loss function 可以记为 \[ L(f) = \sum_n \delta(f(x^n) \ne \hat{y}^n)。 \]
这一个 Loss function 不可微分,不能使用梯度下降的方法解。不用梯度下降的解法可以有感知机或者 SVM 等。
这里介绍另一种方法,也就是基于条件概率的方法。给定类1和类2的概率,以及类1下\(x\)的条件概率,类2下\(x\)的条件概率,然后我们就可以计算,给定\(x\)的情况下,属于类1和类2的条件概率是多少。概率大的那个就是\(x\)最有可能属于的类:
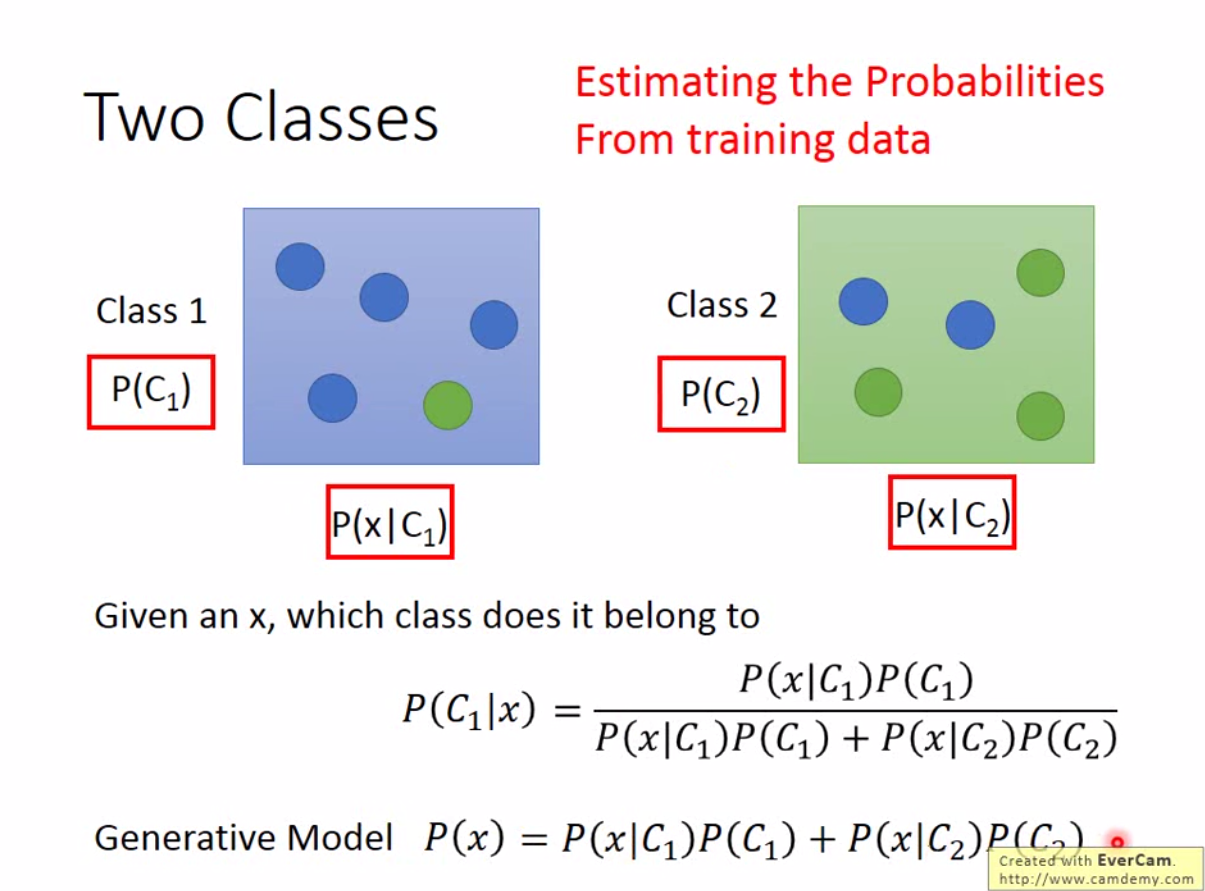
上述方法有一个问题,如果数据不出现在 training data 里,怎么计算在某个类别下,这个 sample 的概率?比如下图中,海龟是 training data 外的数据,那么取到海龟的概率是否记为0?

那其实我们可以假设数据是符合一定分布的,然后去计算在该分布下,出现这个样本的概率。比如现在假设数据符合高维正态分布,这里可以使用极大似然法,也就是找到一组参数\(\mu\)和\(\Sigma\)使得每一个样本的概率乘积最大。
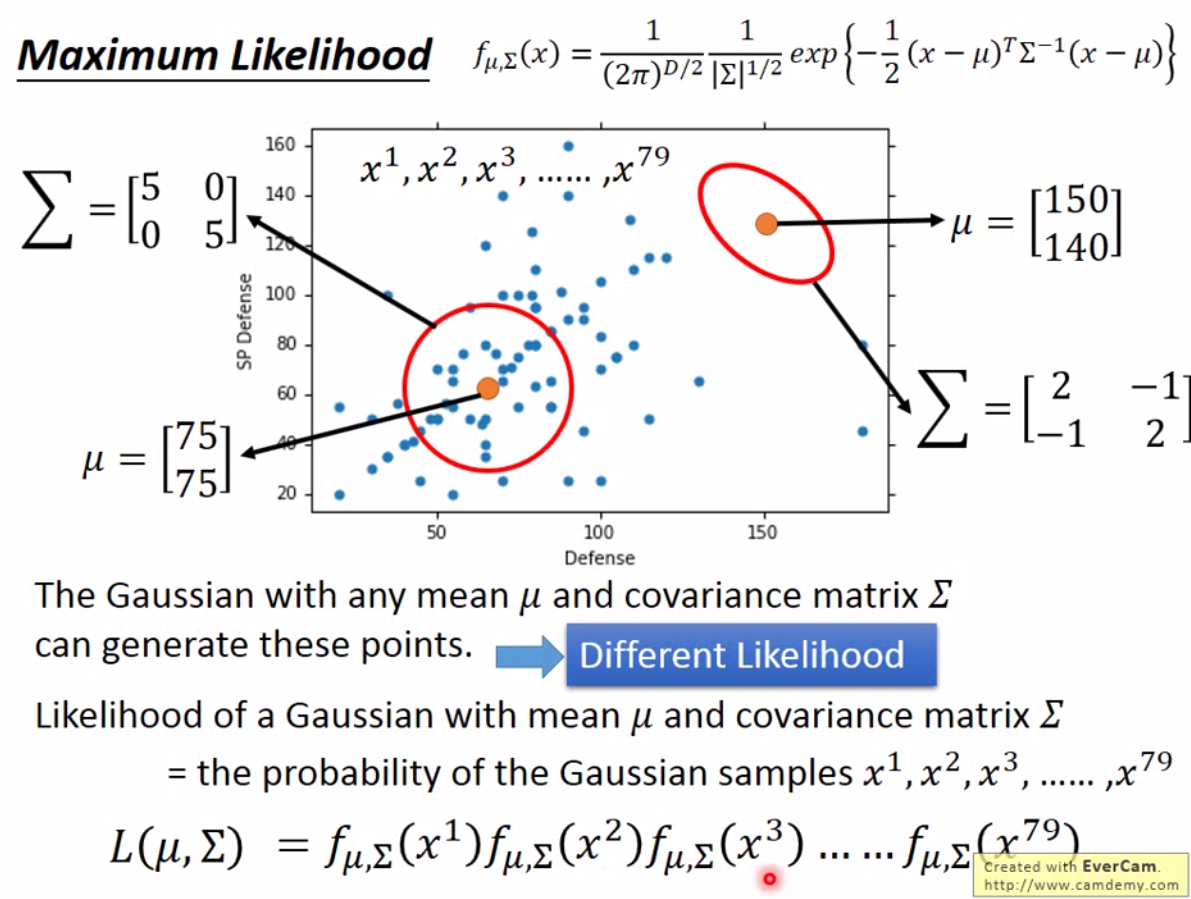
那么要让上面的 Likelihood 最大,就是要找到 \(\mu^*, \Sigma^*\)得到\(\arg \max_{\mu,\Sigma} L(\mu, \Sigma)\)。由于正态分布的概率密度函数在均值处取得最大值,因此相应的均值、标准差可以很直观计算出来。

不过实操上,用上图的计算方法,我们并不会得到一个很好的结果。因为我们没有考虑两个 class 的协方差。所以我们将原来的公式改进为:
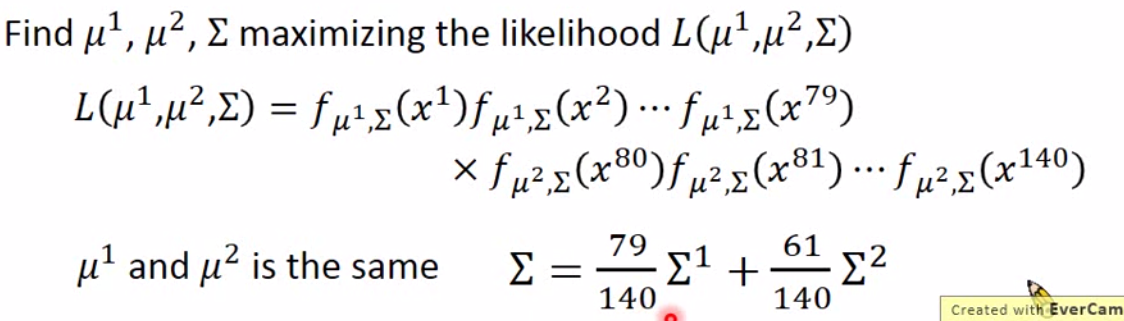
现在的公式就考虑了两个类的协方差,相对来说会比单考虑一个类别的方差效果好。
当然,理论上,这边可以用任意概率分布函数,可以根据实际的数据情况来决定,不过一般来说用正态分布比较多,毕竟好算。
