关于梯度下降的理论基础
梯度下降是要解决这样的一个凸优化问题: \[ \theta^* = \arg \max_{\theta} L(\theta), L \text{ is the object function, }\theta \text{ is parameters}. \] 用向量 \(\bigtriangledown L = \begin{bmatrix} \frac{\partial L}{\partial \theta_1} \\ \frac{\partial L}{\partial \theta_2} \\ \vdots \\ \frac{\partial L}{\partial \theta_n} \end{bmatrix}\) 表示梯度。
为了求解这个目标函数,我们需要按照下面方法更新\(\theta\): \(\boldsymbol{\theta}^1 = \boldsymbol{\theta}^0 - \eta \begin{bmatrix} \frac{\partial L}{\partial \theta_1} \\ \frac{\partial L}{\partial \theta_2} \\ \vdots \\ \frac{\partial L}{\partial \theta_n} \end{bmatrix}.\)
这里我们发现有个\(\eta\)参数。这个参数我们称为 Learning Rate。Learning Rate 本身是机器学习中需要调节的一个重要参数。如果我们将梯度下降当做是爬山,那么Learning Rate我们可以认为是每一次爬山迈的步子大小,而梯度是我们面向的方向。所以很多时候,我们会将learning rate叫做步长。
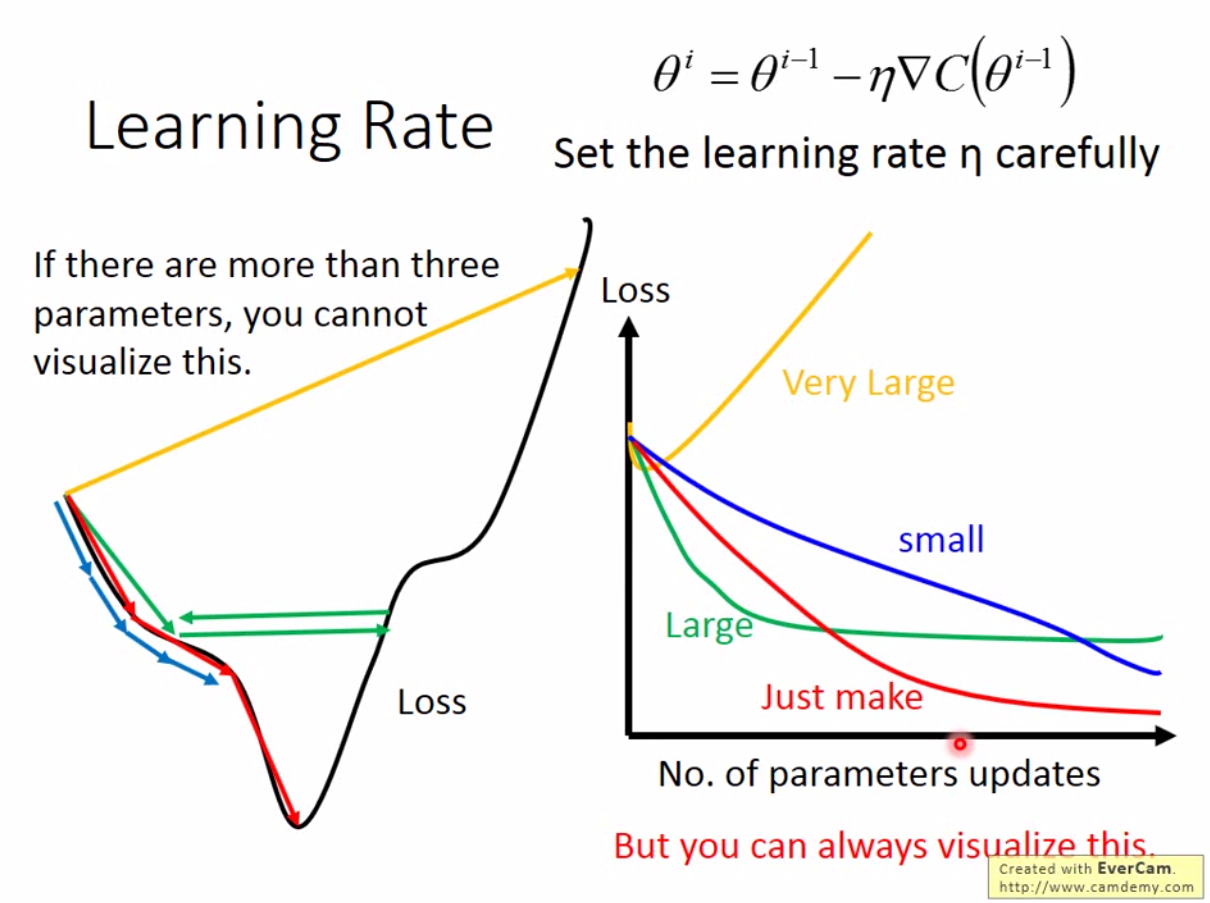
上图显示了,如果我们有个很大的learning rate,那么我们可能会一步跨到更高的地方,或者来回震荡,无法迭代到最优解,相反,很小的 learning rate 可以让你到达最优解,但是将消耗大量的时间。
那么是否有办法来自适应调节 learning rate?
比如,一开始我们通常离最优解很远,那么可以让 learning rate 大一点,随着迭代次数增加,可以减少 learning rate。因此我们可以这样设计 \(\eta^t = \eta^0 / \sqrt{t+1}\)。
事实上有很多种自适应的方法,例如Adagrad,Adam等。李老师介绍了Adagrad。定义为每个 parameter 都去除之前所有的微分的 root mean square。
比如我们有一个参数 \(w\), 原来的梯度下降是这样定义的: \[ w^{t+1} = w^t - \eta^t g^t, \] 而adagrad是: \[ w^{t+1} = w^t - \frac{\eta^t}{\sigma^n} g^t, \] 那 \(\sigma^t\) 就是 \(w\) 在前 \(t\) 步微分的 root mean square。
所以 adagrad 这样更新 \(w\):
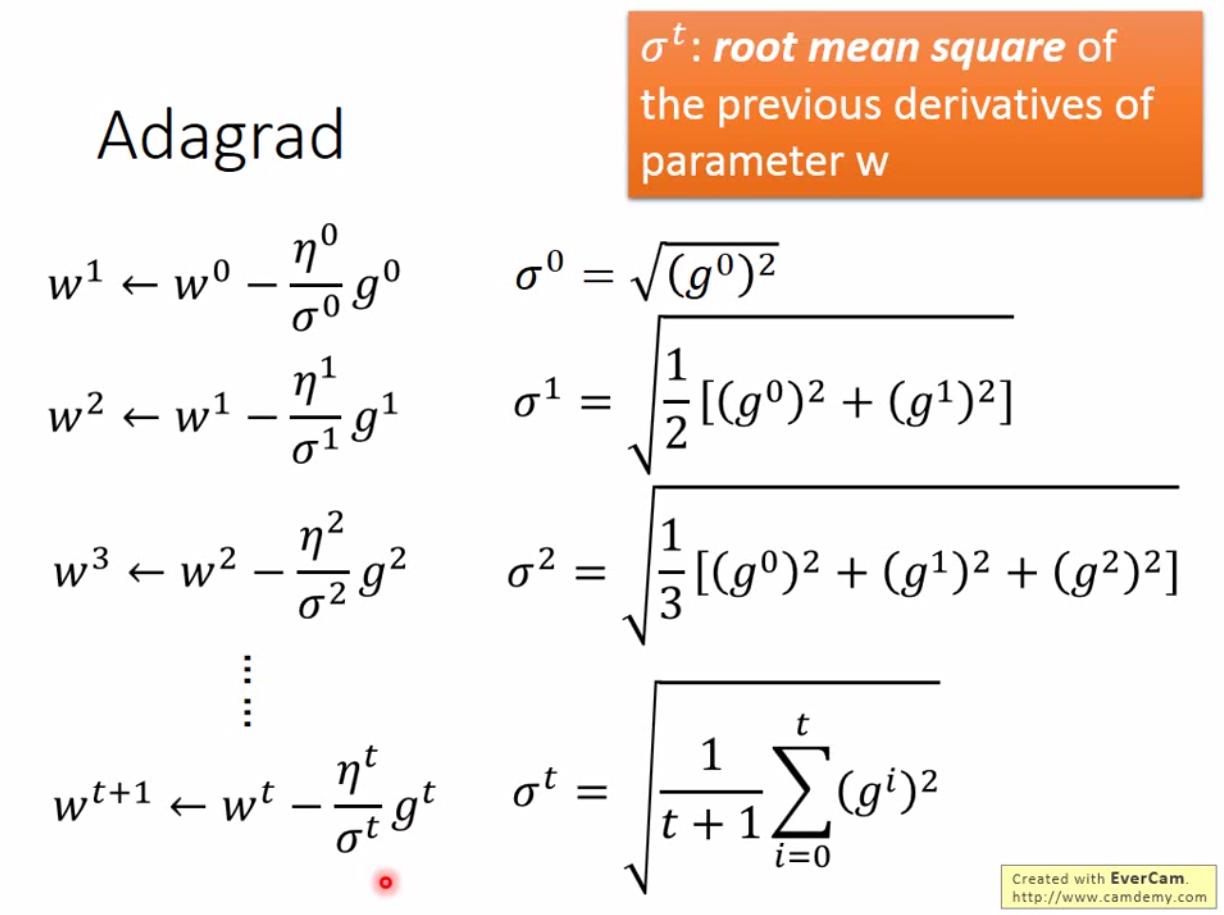
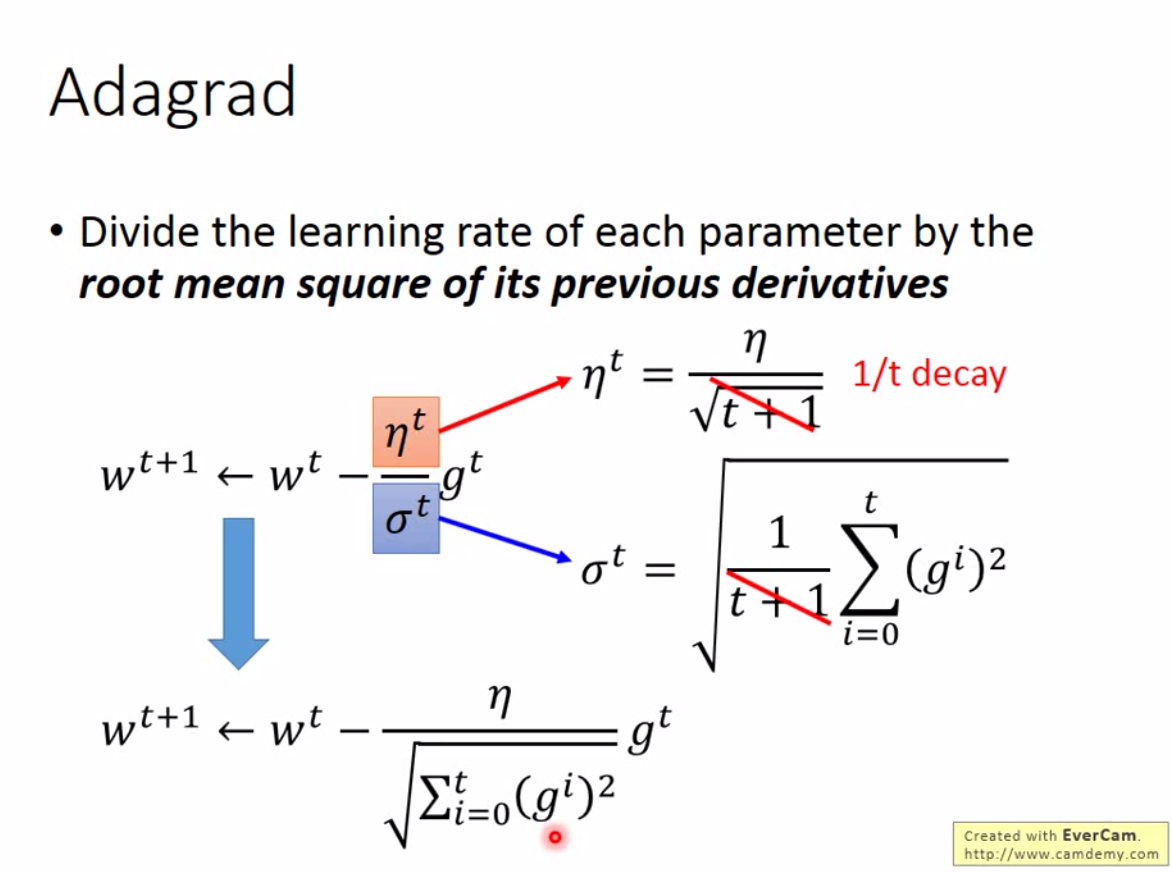
这里要注意一点,adagrad中,梯度算出来越大,说明在这个参数方向上离最优解越远。直观上步长应该越大越快收敛,但是分母部分,梯度越大,步长越小。对于单个参数而言,这没有问题,但是如果现在考虑多个参数,那么梯度越大,不一定离最优解越远。如下图:
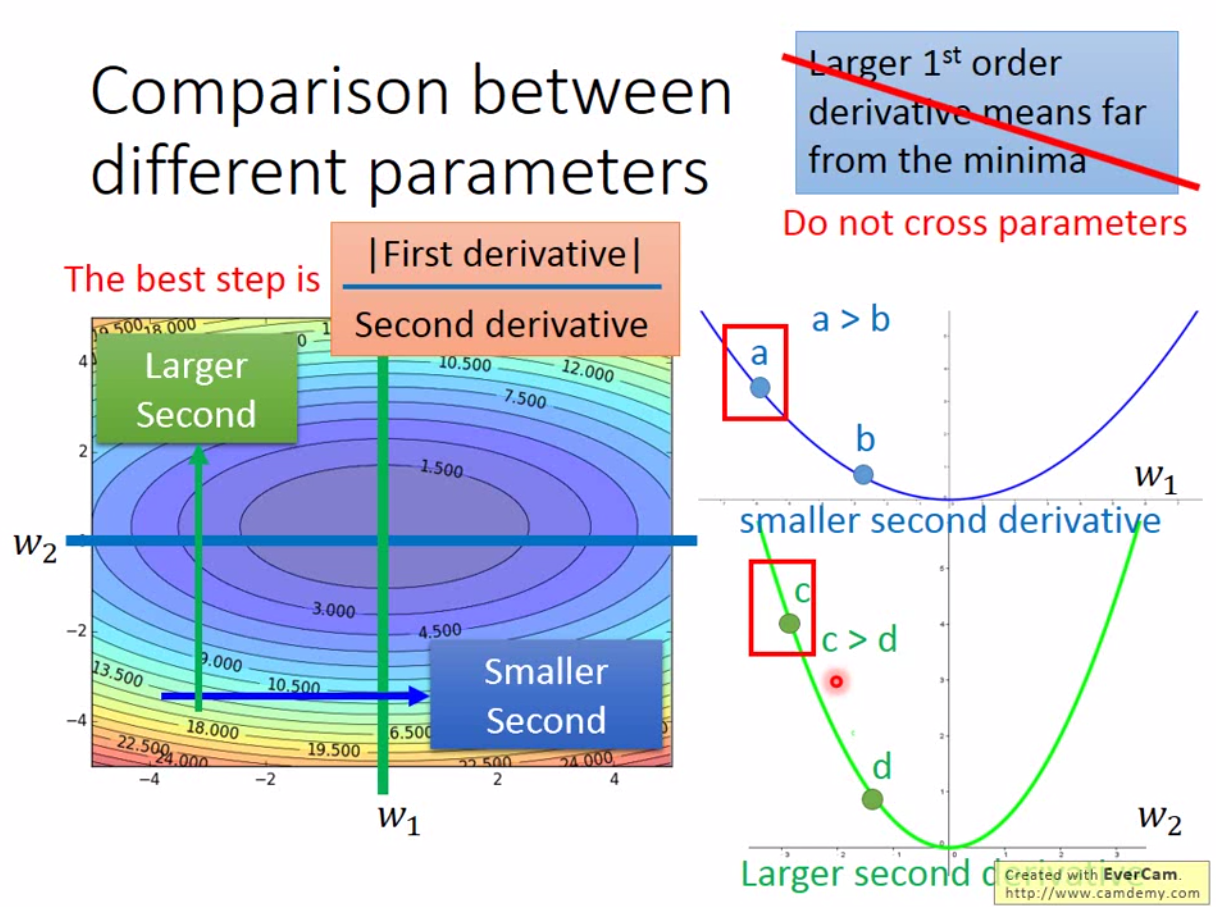
我们看到,绿色的曲线,我们离最优解其实是比较近的,但是梯度很大,这时候如果我们只用一阶导数的话,要走好几步才能走到底。这就跟我们之前想的不太一致了,我们希望步长是慢慢减小的,但是我们希望的是步长在该大的地方大,改小的地方小。所以只考虑一阶段远远不够。
因此最好的 step 应该是还要考虑二次微分,最好的步长是一阶微分的绝对值除以二阶微分,这样才能在不同参数之间比较。
回过头来,adagrad 里面的分母起到的作用就是来替代二阶微分的作用。为什么这样的设计能够work?
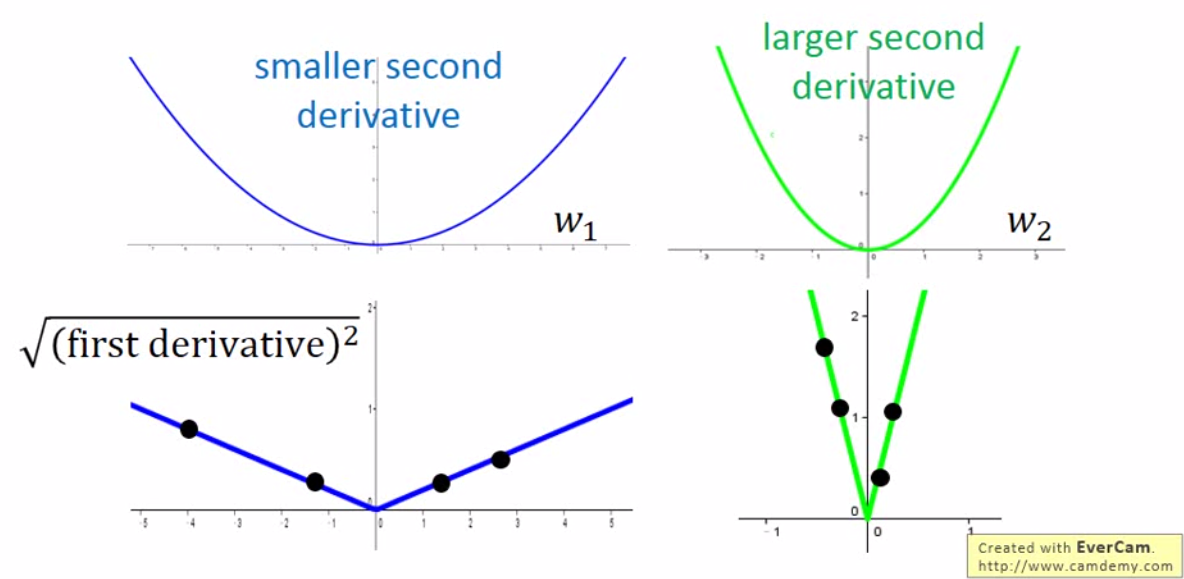
如图所示,我们画出一阶微分的绝对值,只要我们 sample 足够多的数据,我们就能得到,由于二阶微分较小,所以左边的函数一阶微分的 root mean square 就比较小。
那么有没有提高梯度下降效率的方法?一般梯度下降需要遍历整个数据集,而 SGD(Stochastic Gradient Descent)每一次更新仅仅考虑一个 sample 的 Loss。
从图上看,两者的差别就在于 SGD 更散乱,但更快收敛。
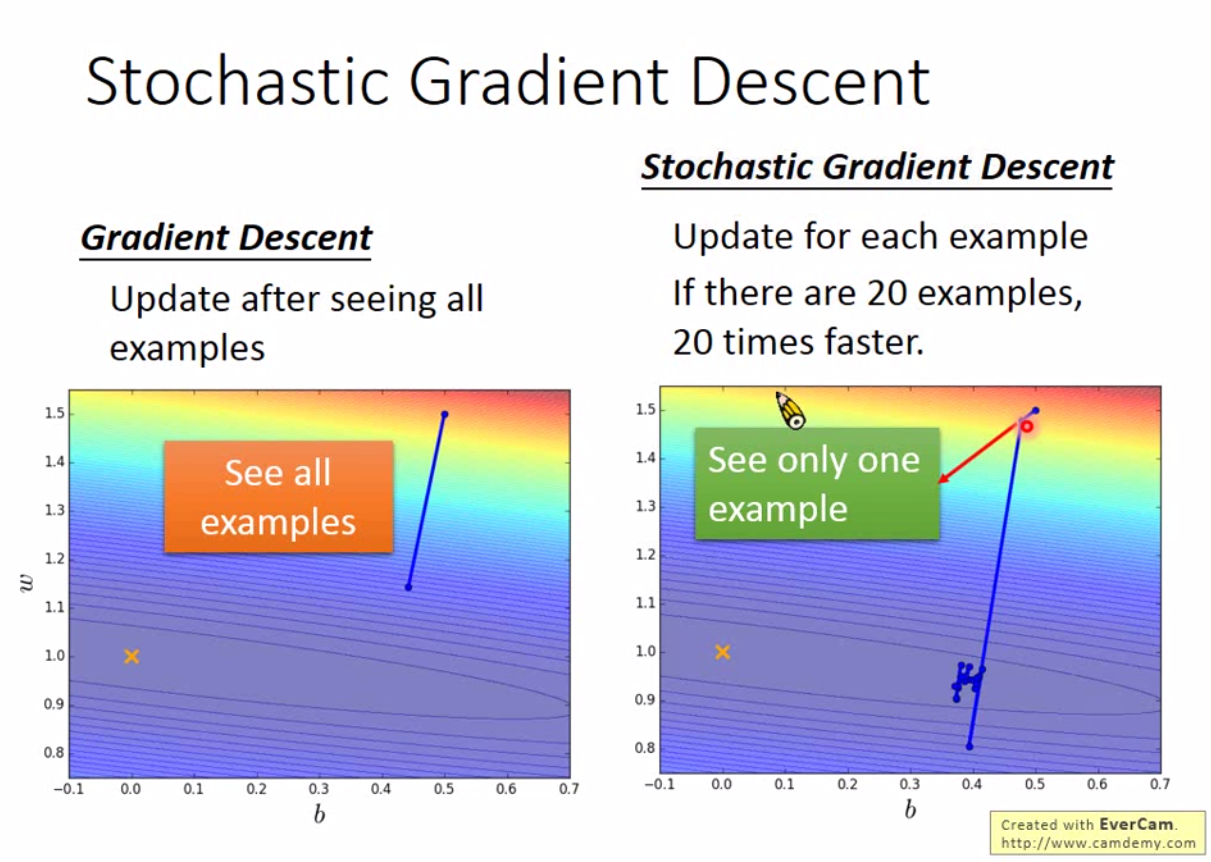
实践上,为了让模型收敛不是太散乱,同时兼顾效率,会考虑使用 mini-batch SGD。也就是说,一次性用一小批数据来更新梯度。
另外一个可以加速收敛的方法是做 feature scaling。考虑下图的情况
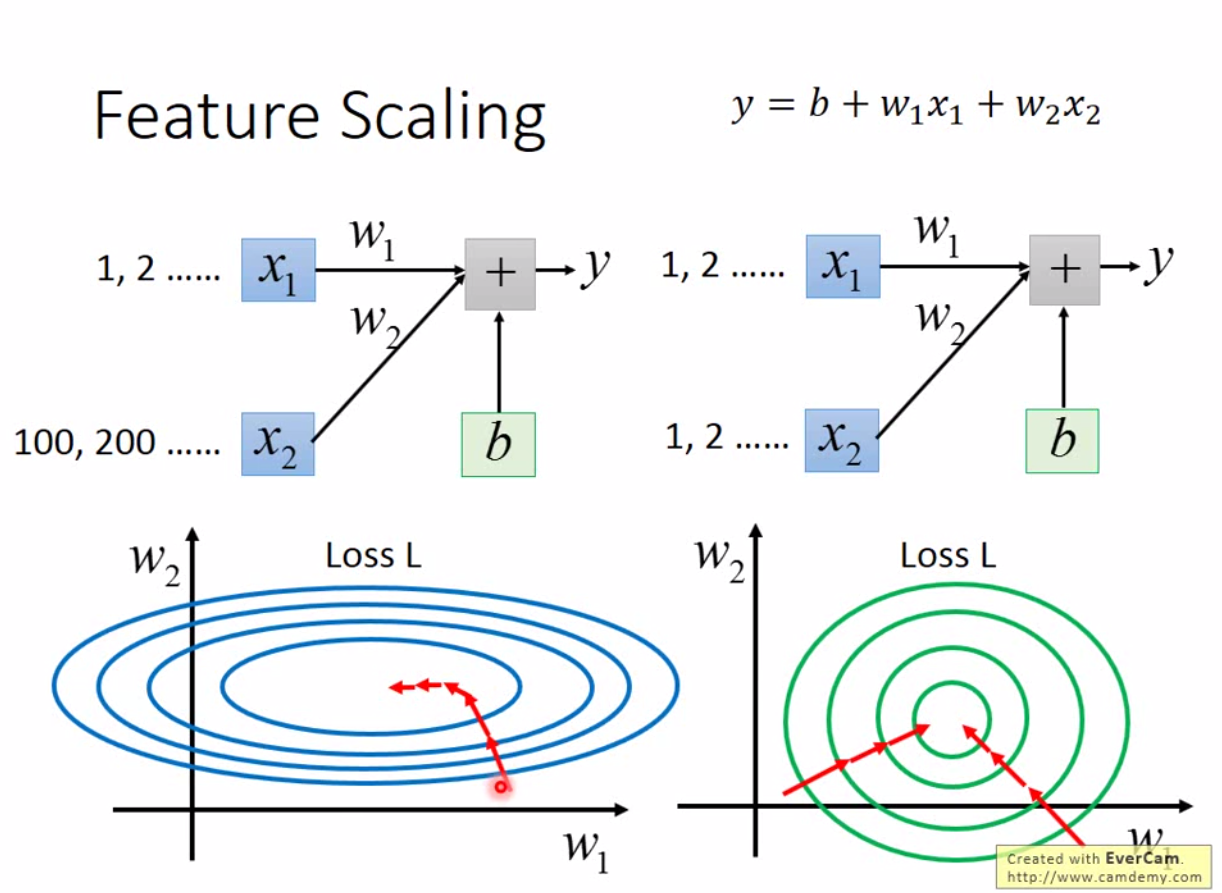
在做 scaling 前,左边的 \(x_2\) 导致 \(w_2\) 的变动对 loss function 的影响非常大,所以左图最后收敛方向都会沿着 \(w_1\) 缓慢下降。因此不用 adagrad 的话,左图的收敛非常慢。而右图因为接近正圆形,沿着任意方向都能快速接近最优解。
那么 scaling 方法有哪些?常见的比如 z-score,0-1标准化等。这个也叫作normalization。
这里开始讨论梯度下降的数学原理。
梯度下降可以成立是基于泰勒展开,Taylor series。那么函数可以写成: \[ \begin{align} h(x) &= \sum_{k=0}^{\infty} \frac{h^{(k)}(x_0)}{k!}(x-x_0)^k \\ &= h(x_0) + h'(x_0)(x-x_0)+\frac{h''(x_0)}{2!}(x-x_0)^2+\dots \end{align} \] 当 \(x\) 无限趋近于 \(x_0\) 时候,我们取一阶泰勒展开就可以近似估计原函数。相应的,如果原函数是个多元函数,那么相应的将导数改成偏导数就可以。
那么,基于泰勒公式,我们的 Loss function 就可以用泰勒展开为一阶多项式。
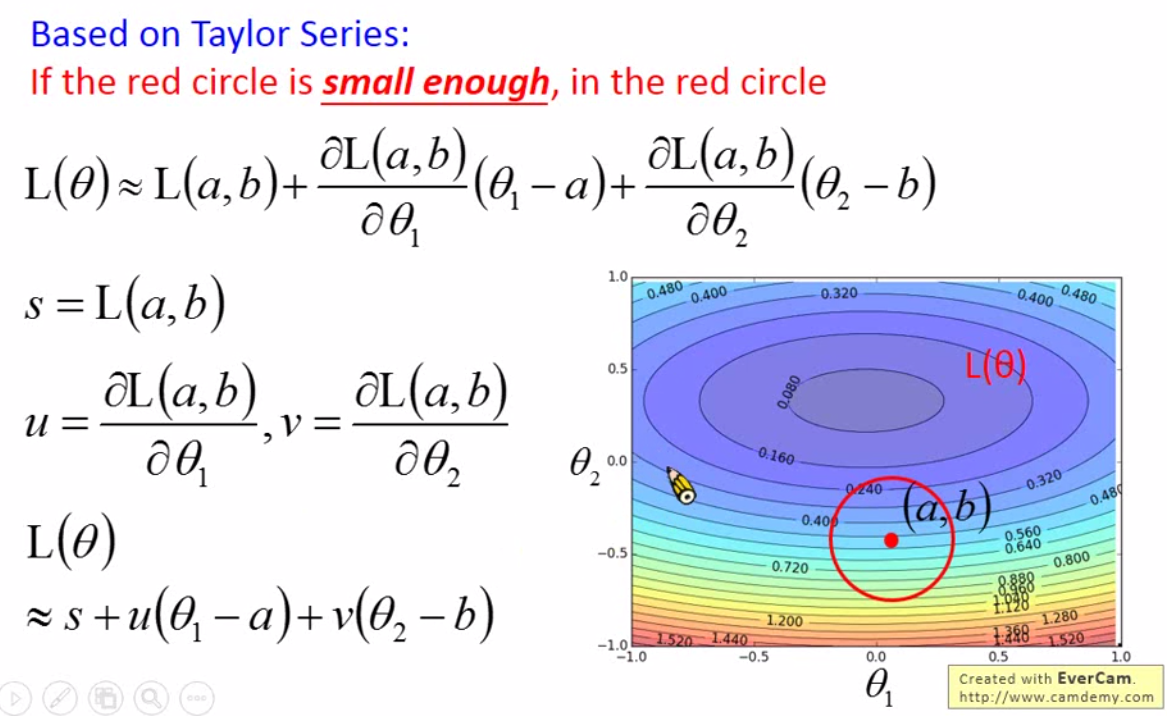
那么在图上一个红色的圆圈内,如何让 Loss 最小?我们可以发现,Loss 只跟两个向量有关,一个是\((u, v)\),另一个是\((\theta_1 - a, \theta_2 - b)\)。我们用\((\Delta \theta_1\), \(\Delta \theta_2)\) 表示第二个向量。
因此我们可以知道,要让Loss最小,就是上述两个向量的内积最小,也就是找\((u, v)\)反方向上长度最长的向量: \[ \begin{bmatrix} \Delta \theta_1 \\ \Delta \theta_2 \end{bmatrix} = -\eta \begin{bmatrix} u \\ v \end{bmatrix} \] 也就是 \[ \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix} = \begin{bmatrix} a \\ b \end{bmatrix} - \eta \begin{bmatrix} u \\ v \end{bmatrix} \]
优化方法有很多,之前博客里面写的遗传算法,退火算法,蚁群算法等都是,但是 mini-batch SGD 是目前最常用的方法,因为效率极高。但是这不意味着 SGD 就是最好的方法,因为这是一个很典型的贪心算法,大部分情况下只能接近局部最优。 如下图:
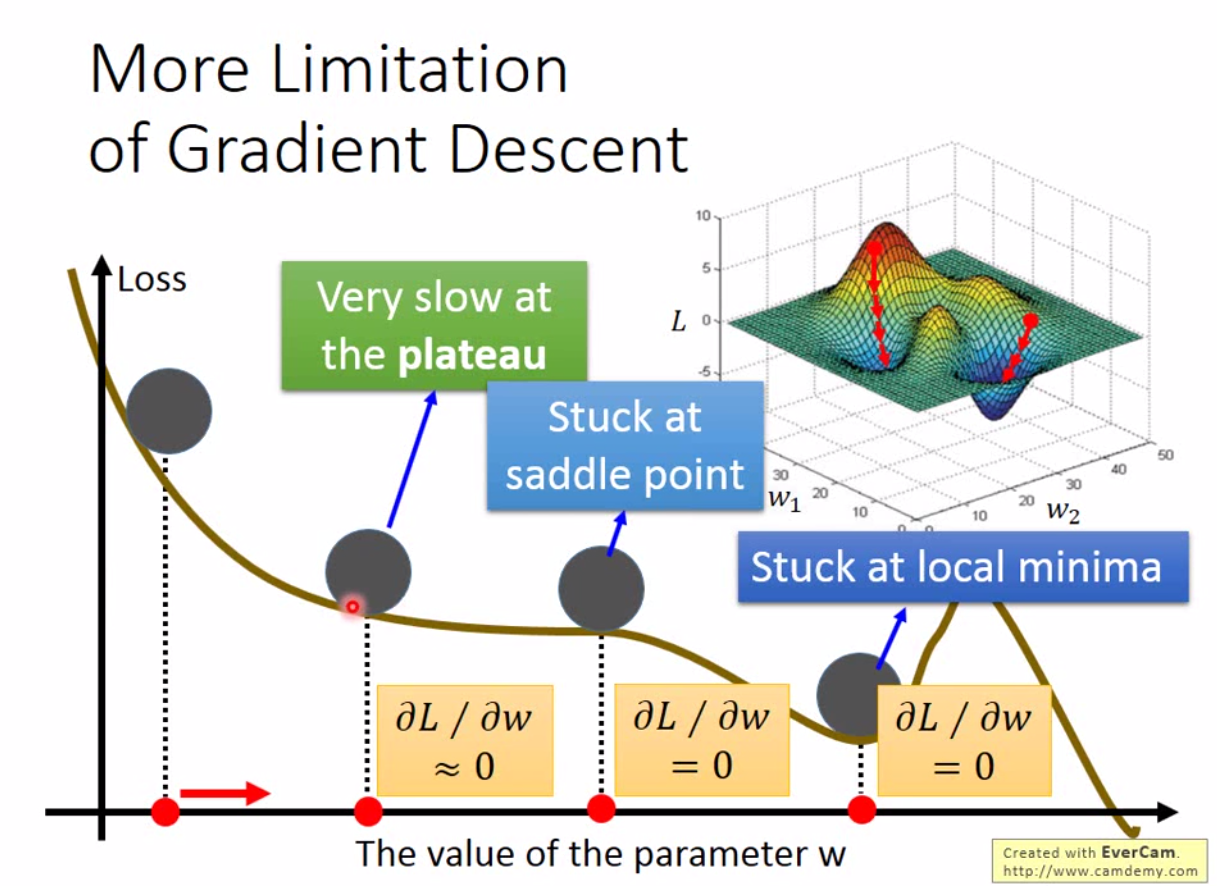
通常我们发现梯度下降很慢的时候,就会停止迭代了,但实际上,可能我们离局部最优都很远,更不用说全局最优。深度学习常见的一个坑。
