现在我们来看看误差从何而来
模型误差来源于 bias and variance.
假设有一组数据 \(x\), 均值是 \(\mu\),方差是 \(\sigma^2\)。
我们现在估计均值。抽样 N 个样本 \(\{x^1, x^2, \dots , x^N \}\), 那么我们的均值就是\(m = \frac{1}{N} \sum_n x^n \ne \mu\)。也就是说,一般而言,我们抽样得到的均值并不会严格等于数学期望。但是 \(E(m) = E\Big(\frac{1}{N} \sum_n x^n \Big) = \frac{1}{N} \sum_n E(x^n) = \mu\) 且 \(Var(m) = \frac{\sigma^2}{N}\)。这说明,当我们抽样的数据越多,我们的样本均值越接近总体的期望,bias越小。
现在估计方差。同样抽 N 个样本, \(\{x^1, x^2, \dots , x^N \}\)。样本方差\(s^2 = \frac{1}{N} \sum_n(x^n - m)^2\)。这是一个有偏估计,样本方差的期望是\(E(s^2) = \frac{N-1}{N} \sigma^2\),同样当抽样的数据越多,越接近总体的方差,bias越小。
因此,模型的bias就是估计值的中心点到实际值中心点的距离,也就是\(E(\hat{y})\)到\(E(y)\)的距离,而模型的方差就是各个估计点\(\hat{y}\)到其中心点\(E(\hat{y})\)的距离。
那我们只有一组数据,为什么会有方差呢?实际上当我们抽样不同的数据,就会得到不同的模型,这样我们的估计值就会不同。所以模型存在方差(这已经是集成算法方面的东西了,bagging、boosting这一类的方法)。
现在假设我们抽样 5000 次,模型的复杂度和错误率会是什么样的关系呢?
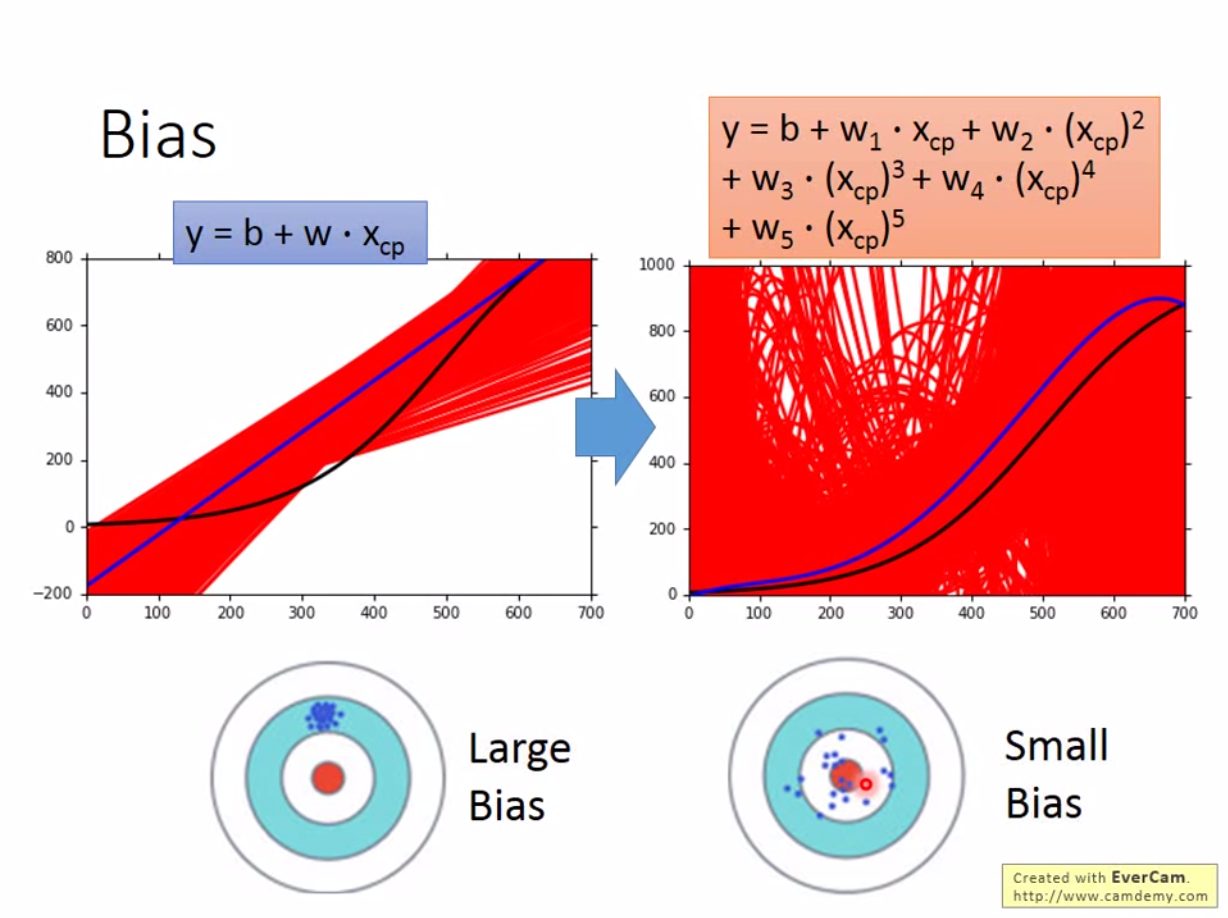
如上图,当模型复杂度较低的时候,模型的variance很小,但是bias很大。当模型复杂度很高的时候,模型的variance很大,但是bias很小。
那么我们要如何解决这个问题?
如果我们的模型有很大的bias,那么我们应该增加模型的复杂度,或者增加模型的feature。
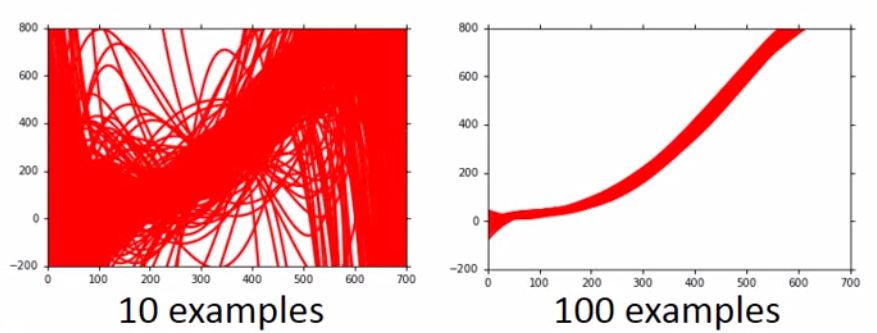
如果我们模型的variance很大,那么应该增加样本数量,或者做regularization。如下图,我们抽了100个样本,那么variance比10个样本的小很多。
而不增加样本,直接做regularization如下:
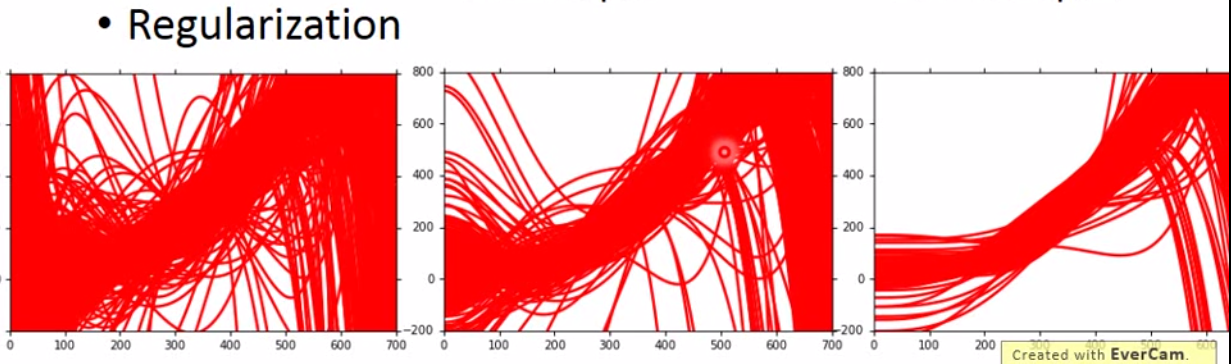
但是我们需要注意到一点,regularization越大,bias会越大,因为模型复杂度降低了。这是一个trade-off。所以我们需要将数据分为 training 和 testing。一个比较有用的方法是 cross validation。它的原理如下:
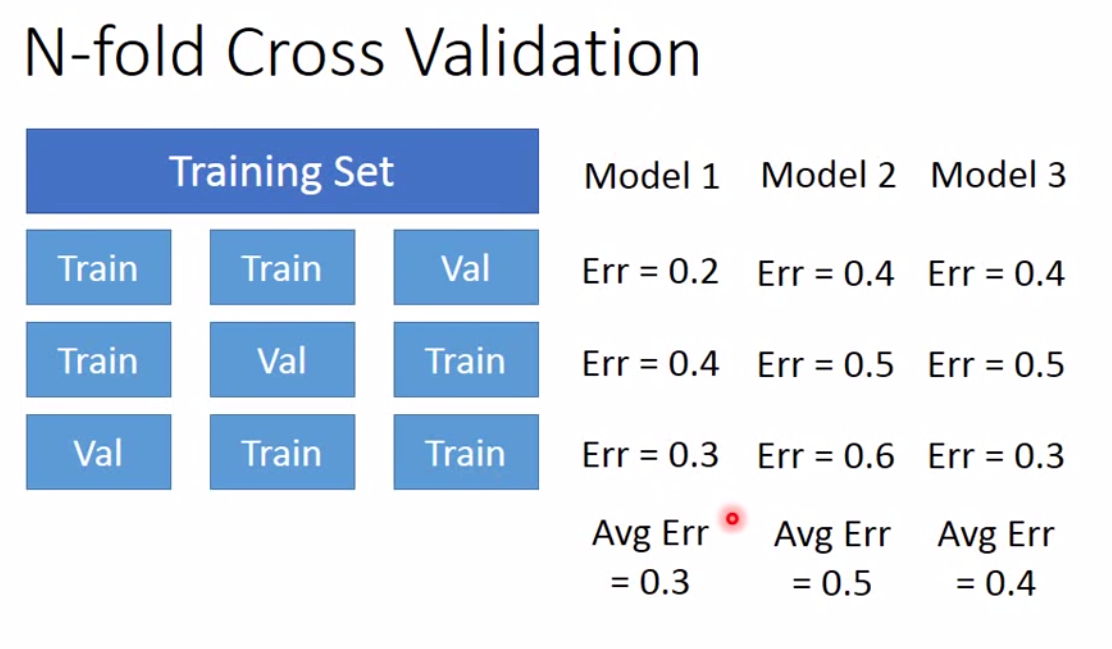
建模的禅道就是,别太在意training的效果,有时候validation和testing的效果反而不错。另外训练模型要注意的一点是,不要针对testing set做调优,否则会过拟合。
