集成算法基本上现在已经成为机器学习的标准套路,单一模型的几乎已经销声匿迹。集成算法有两大分类,一类是bagging,一类是boosting。
bagging
bagging是一种比较简单的集成策略,做法就是原来有\(N\)个sample,现在sample出\(N'\)个sample,重复这样的动作多次,就可以得到很多个模型,然后如果是regression就做average,如果是classification就做voting。所以这样的策略是非常非常简单的。那这么做的目的其实是为了降低复杂模型的variance。这个可以回过头看之前的内容。所以bagging并不会解决overfitting,也不会起到什么加强模型预测能力的效果。只能说,用bagging的方法,模型会比较平滑。
那什么模型非常复杂容易overfitting呢?其实决策树是最容易overfitting的算法,NN反而没有那么容易overfitting,只是说NN建的模型多,variance比较大一点而已。
这边有个实验数据,这个数据是miku的一个黑白图,如果正确分类就可以画出miku。
如果我们用一个单一模型,我们得到的是:
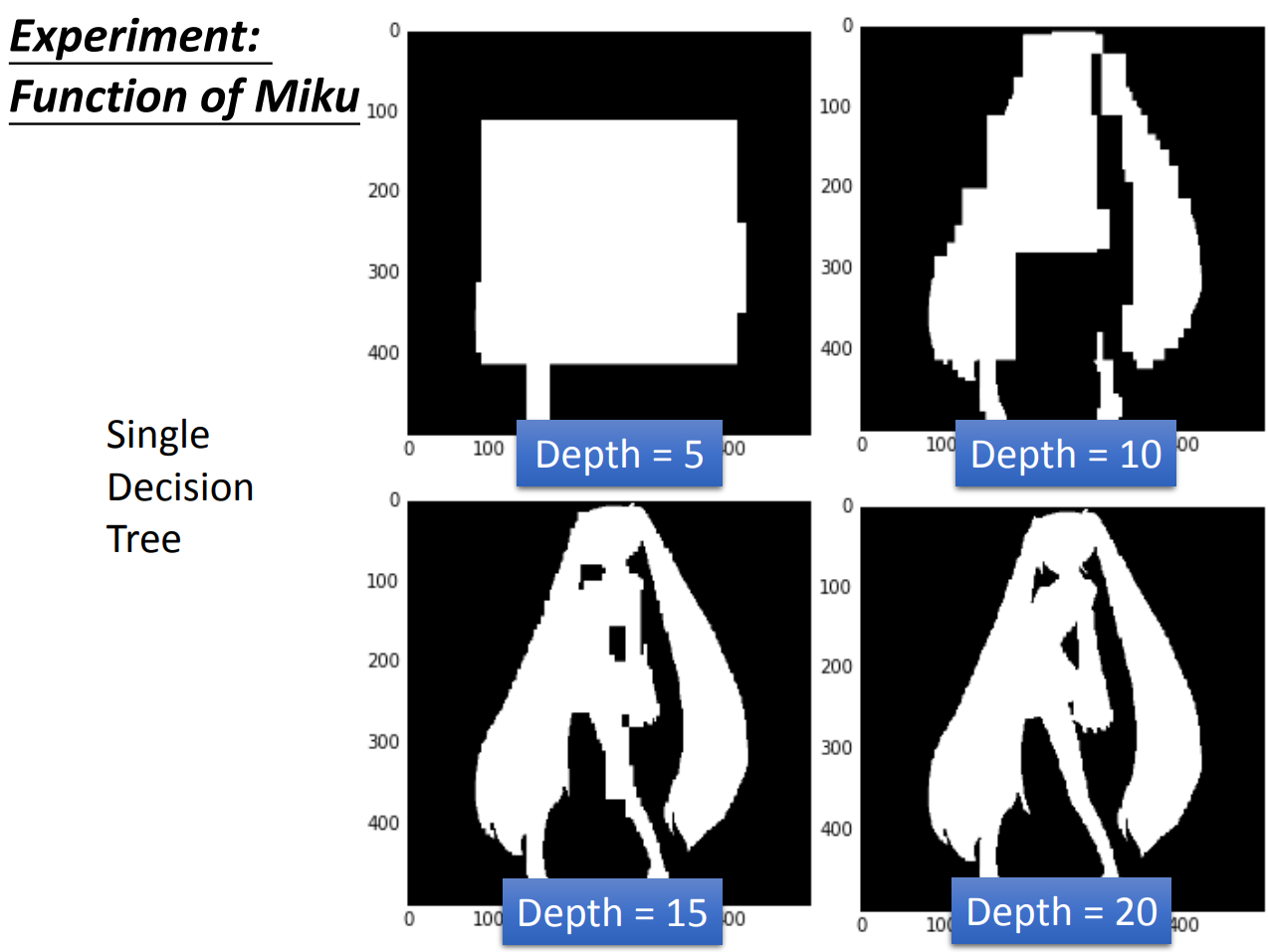
当树深度一点点增加到20层的时候,就可以完美画出miku。
那如果用bagging,也就是random forest的方法,我们得到的是:

我们可以跟上面的结果做一个对比,可以发现,单一的树画出来的miku没有那么平滑。用random forest画出来的结果相对比较平滑。
boosting
boosting是比bagging要强大的一种策略,bagging只是平滑复杂函数,而boosting是将大量的弱分类器集成为一个强分类器。adaboost是boosting算法里面的典型。
adaboosting的策略是,首先建一个分类器\(f_1(x)\),然后根据\(f_1(x)\)的分类结果,错误分类的样本权重变大,正确分类的样本权重调低,调整到正确率差不多50%,然后这样re-weighted的结果拿来训练第二个分类器\(f_2(x)\)。这样一直重复多次,将这些弱分类器都combine起来就是最终的强分类器。这里要跟bagging对比一下,boosting是没有resample数据的,只是改变了weight。那么现在的大杀器xgboost和lightgbm其实都是站着前人的基础上,继承了boosting和bagging的特性,也可以在boosting的时候做bagging的事情。
下图是我们做boosting的一个示意:

我们一开始所有样本的weight都是一致的,训练了一个分类器,错误率\(\varepsilon_1 = 0.25\),我们重新修改weight,把错误分类的weight改到\(\sqrt{3}\),正确分类的修改到\(\frac{1}{\sqrt{3}}\),我们就可以把错误率调到\(\varepsilon_1' = 0.5\)。然后我们用这个新的weight来训练第二个模型,如此循环往复。
数学上来看这件事情是这样的,原本我们的loss function是\(\frac{\delta(f_1(x) \ne \hat{y}^n)}{n}\),加权的loss function是\(\frac{\sum_n u_n^1 \delta(f_1(x_n) \ne y_n)}{\sum_n u_n}\)。这里做了一个归一化,因为所有的weight加起来未必等于1。然后要做的事情就是调整\(u_i^1\)使得\(u_i^2\)能让\(f_1\)失效。不断的迭代其实就是把\(u_i^{t-1}\)调整到\(u_i^{t}\),使得上一个模型失效。那实际上就是当\(t\)轮模型进行预测,分类正确,weight除以\(d^t\),分类错误weight乘以\(d^t\)。
那么每一步的\(d\)应该是多少呢?因为我们要保证这个数可以让函数的误分类率刚好被调整到0.5左右。我们可以推导一下,其实非常简单。首先科普一下\(\delta\)函数,这里的\(\delta (f(x), y)\)表示的是,当\(f(x) = y\)时为0,不等为1。所以我们可以知道\(\varepsilon_1到\varepsilon_2\)的过程中,分类正确的\(u_i\)全变成\(u_i^1 / d^1\),错误的变成\(u_i^1 \times d^1\)。所以原来的结果是: \[ \varepsilon_1 = \frac{\sum_n u_n^1 \delta(f_1(x_n) \ne y_n)}{\sum_n u_n^1} \] 现在的结果是: \[ \varepsilon_2 = \frac{\sum_n u_n^2 \delta(f_2(x_n) \ne y_n)}{\sum_n u_n^2} \] 那么其中的\(\sum_n u_n^2 = \sum_{f(x) = y} u_n^1 / d^1 + \sum_{f(x) \ne y} u_n^1 \times d^1\)。而分子部分就等于\(\sum_{f(x) \ne y} u_n^1 \times d^1\)。现在我们要\(\varepsilon_2 = 0.5\),可以知道,就是让\(\sum_{f(x) \ne y} u_n^1 \times d^1 = \sum_{f(x) = y} u_n^1 / d^1\)。因为\(d^1\)是常数,可以提取出来,然后\(\sum_{f(x) = y} u_n^1 = \sum_n u^1_n (1-\varepsilon_1),\sum_{f(x) \ne y} u_n^1 = \sum_n u^1_n \varepsilon_1\)。刚好\(\sum_n u^1_n\)又是常数,再消掉,我们可以轻松得到\(d^1 = \sqrt{\frac{1-\varepsilon_1}{\varepsilon_1}}\)。这里我们需要做乘法和除法,虽然对程序而言问题不大,但是公式上不是那么好看。我们可以将这个系数改成\(a^t = \ln(d^t)\)这样一来,我们就可以把公式改成 \[ u^{t+1}_n = u^t \times \exp(-a^t) \text{ if } f(x) = y \\ u^{t+1}_n = u^t \times \exp(a^t) \text{ if } f(x) \ne y \] 然后我们又发现,如果我们做二分类的问题,我们可以将\(y\)的取值改为\(\pm 1\),这样一来,我们上面的公式就可以化简到一个非常舒服的样子: \[ u^{t+1}_n = u^t \times \exp(- y f_t(x) a^t) \]
那么adaboost基本上的工作原理就是这样。那么最后我们得到的分类函数就是之前所有弱分类器的集成版: \[ H(x) = \text{sign}(\sum^T_t a^t f_t(x)) \]
现在的问题就是,adaboost为什么可以收敛呢?我们知道adaboost的error rate函数是 \[ \frac{1}{N} \sum_n \delta(H(x_n) \ne y_n) \] 我们定义一个函数\(g(x) = \sum_{t=1}^T a^t f_t(x)\),那上面的式子实际上就是 \[ \frac{1}{N} \sum_n \delta(y_n \times g(x_n) < 0) \] 然后这里我们定一个exponential loss function,就是\(\exp(-y_n \times g(x_n))\)。这里很直觉的,错误率函数是小于等于这个,所以我们可以得到: \[ \frac{1}{N} \sum_n \delta(y_n \times g(x_n) < 0) \le \frac{1}{N} \sum_n(\exp(-y_n \times g(x_n))) \] 实际上这个upper-bound是非常宽松的一个限制,只要让这个upper-bound收敛,那么我们的错误率就一定会收敛。
怎么做到呢?我们回过头看之前的数据,在更新\(u^t\)的时候,我们用到了\(\exp(-y_n f_t(x_n))\),而\(g(x)\)是\(f(x)\)的最终加权平均的集成版,所以我们尝试将所有的\(u\)加起来会怎么样?所有的\(u\)加起来我们用\(Z\)表示,因为\(u_1 = 1\),\(u_{t+1} = u_t \exp(-y f_t(x) a_t)\),这是一个等比数列,所以 \[ u_{T+1} = \prod_{t=1}^T \exp(-y f_t(x) a_t) \] 所以 \[ \begin{align} Z_{T+1} &= \sum_n \prod_{t=1}^T \exp(-y_n f_t(x_n) a_t) \\ &= \sum_n \exp (-y_n \sum_{t=1}^T(f_t(x_n) a_t)) \end{align} \] 然后我们发现,尾巴部分的其实就是\(g(x)\)。于是我们就把上面的upper-bound跟\(Z\)统一了起来,得到: \[ \frac{1}{N} \sum_n \delta(y_n \times g(x_n) < 0) \le \frac{1}{N} \sum_n(\exp(-y_n \times g(x_n))) = \frac{1}{N} Z_{T+1} \] 然后要证明的就是\(Z_{T+1}\)会越来越小。
因为 \[ \begin{align} Z_{t+1} &= Z_{t} \varepsilon_t \exp(a_t) + Z_{t} (1 - \varepsilon_t) \exp(-a_t) \\ &= Z_{t} \varepsilon_t \sqrt{\frac{1-\varepsilon_t}{\varepsilon_t}} + Z_{t} (1 - \varepsilon_t) \sqrt{\frac{\varepsilon_t}{1 - \varepsilon_t}} \\ &= 2 \times Z_{t} \times \sqrt{\varepsilon_t(1-\varepsilon_t)}。 \end{align} \] 所以我们可以 得到\(Z_{T} = N \prod_{t=1}^T 2 \sqrt{\varepsilon_t(1-\varepsilon_t)}\)。因为\(\varepsilon\)只有刚好取到0.5的时候才会等于1,否则会一路收敛,越来越小。
然后我们可以看到gradient boosting这种方法。事实上,gradient boosting优化的方向不再是对样本,而是直接作用于function。如果我们现在接受一个function其实就是一个weight的vector,那么其实我们就是可以对function求偏导的。我们从梯度下降的角度来看这个问题,那么我们在做的事情就是 \[ g_t(x) = g_{t-1}(x) - \eta \frac{\partial L}{\partial g(x)} |_{g(x) = g_{t-1}(x)} \] 但是换个角度,从boosting的角度来看,我们其实boosting的过程是每一次找一个\(f_t(x)\)和\(a_t\),使得最终的模型\(g_t(x)\)更好。这个过程就是: \[ g_t(x) = g_{t-1}(x) + a_t f_t(x) \] 考虑到跟上梯度的过程,我们可以知道,其实我们希望梯度的方向跟我们boosting优化的方向最好能够是一样的。如果这里我们的loss function选择的是exponential loss,那么loss function就是\(\sum_n \exp(-y_n g(x_n))\), 梯度就是\(\sum_n \exp(-y_n g(x_n))(-y_n)\),刚好跟梯度前面的负号抵消掉。在这种情况下,如果要让二者的方向一样,我们可以用这样的公式来表示: \[ \sum_n \exp(-y_n g_{t-1}(x_n)) y_n f_t(x) \] 当这个公式越大,表示二者的方向越一致。在adaboost中,\(\sum_n \exp(-y_n g_{t-1}(x_n))\)这个刚好就是我们在\(t\)轮得到的样本权重。
回到损失函数这里,我们的损失函数是: \[ \begin{align} L(g) &= \sum_n \exp(-y_n g_t(x_n)) \\ &= \sum_n \exp(-y_n (g_{t-1}(x_n) + a_t f_t(x_n))) \\ &= \sum_n \exp(-y_n g_{t-1}(x_n)) \exp(-y_n a_t f_t(x_n)) \\ &= \sum_{f_t(x) \ne y} \exp(-y_n g_{t-1}(x_n)) \exp(a_t) + \sum_{f_t(x) = y} \exp(-y_n g_{t-1}(x_n)) \exp(-a_t) \end{align} \] 我们希望得到的是\(\frac{\partial L}{\partial a_t} = 0\),因为 \[ \begin{align} L &= \sum_n \exp(-y_n g_t(x_n)) \\ &= Z_{t+1} \\ &= Z_t \varepsilon_t \exp(a_t) + Z_t (1-\varepsilon_t) \exp(-a_t) \end{align} \] 前面的系数\(Z_t\)跟\(a_t\)没关系直接消掉,然后求导数我们得到的就是: \[ \frac{\partial L}{\partial a_t} = \varepsilon_t \exp(a_t) - (1-\varepsilon_t) \exp(-a_t) = 0 \] 这样我们就可以求出来\(a_t = \ln \sqrt{\frac{1-\varepsilon_t}{\varepsilon_t}}\)刚好就是adaboost。
实际上gradient boosting是可以改变loss function的,adaboost就是一个特殊的gradient boosting。台大另一个老师,林轩田的课程里面是有更general的介绍。
