机器学习的算法太多了,但是很多算法之间的差异实际上不大。SVM是曾经风靡一时,一度虐杀神经网络的算法,不过DL出现以后,没落了不少啊。真是三十年河东三十年河西。
这里简单学习一下SVM。SVM跟其他的机器学习算法的差别在于,第一,loss function不一样,第二,有一个kernel function。其中的kernel function是大杀器。
现在我们假想我们要学的是一个二分类的问题,我们回顾一下几种损失函数。最开始的时候,我们学的是平方误差,也就是MSE,在二分类问题上,我们想要达到的效果就是当\(y=1\)的时候,\(f(x)\)越接近1越好,同理,\(y=-1\)的时候,\(f(x)\)越接近-1越好。那么基于square error,我们可以得到: \[ \begin{cases} (f(x) - 1)^2 & \mbox{if } y = 1 \\ (f(x) + 1)^2 & \mbox{if } y = -1 \end{cases} \] 那其实上面两个式子可以统一成\((yf(x) - 1)^2\)。
那逻辑回归的loss function是cross entropy,那实际上也可以写作是\(\ln(1+\exp(-yf(x)))\)。之前的adaboost的loss function我们也可以用exponential loss来表示,也就是\(\exp(-yf(x))\),那么我们将这几种loss function跟最简单的\(\delta(f(x) \ne y)\)对比一下:
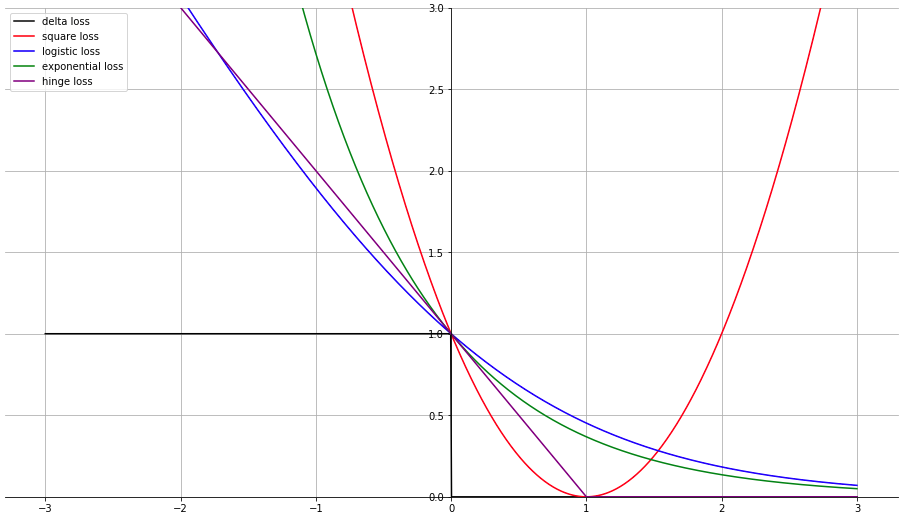
那我们回过头看一下,如果是用\(\delta\)函数,那么我们根本就没有办法求梯度。而如果我们用square loss,我们可以发现,左右两边的loss都很大,但是实际上,当\(f(x)\)跟\(y\)的方向一致,两个乘积非常大,本质上loss应该趋近于0才对,所以square loss不是非常合适。那另外的logistics loss跟exponential loss,都可以做到越远越好。另外这里需要注意一下,为了让logistics loss能够成为\(\delta\)函数的upper bound,我们会将原来的公式除以\(\ln 2\)。
那么SVM呢?SVM用的是hinge loss,hinge loss表示为:\(\max(0, 1-yf(x))\)。那hinge loss的一个好处就是,当\(f(x)\)跟\(y\)一致,就可以了,那么hinge loss的好处就是,hinge loss对异常值比较不敏感,差不多就好了,而cross entropy跟exponential loss都会拼命去拟合异常值。
那linear SVM实际上就是logistics regression把loss function换成hinge loss。所以假设也是: \[ f(x) = \sum_i w_i x_i + b \] 而loss function就是: \[ L(f) = \sum_n(l(f(x_n), y_n)) + \lambda \|w_i\|_2 \] 那么,实际上,如果我们神经元用了一个linear SVM,一样也是可以做deep learning的。所以,嗯,别整天BB自己在做DL,好好学基础再BB。
那么SVM的loss function不是处处可微分的,有没有可能做梯度下降呢。实际上,DL中的ReLU函数都可以,所以SVM实际上也是可以做的。那求导的过程是这样的: \[ \frac{\partial l(f(x_n), y_n)}{\partial wi} = \frac{\partial l(f(x_n), y_n)}{\partial f(x_n)} \frac{\partial f(x_n)}{\partial w_i} \] 那其实\(\frac{\partial f(x_n)}{\partial w_i}\)就是\(x_n^i\)。
那\(\frac{\partial l(f(x_n), y_n)}{\partial f(x_n)}\)怎么计算呢,这是一个分段函数,所以分段求导: \[ \frac{\partial \max(0, 1 - y_n f(x_n))}{\partial f(x_n)} = \begin{cases} -y_n & \mbox{if } y_n f(x_n) < 1 \\ 0 & \mbox{if } y_n f(x_n) \ge 1 \end{cases} \] 所以实际上linear SVM的梯度就是: \[ \frac{\partial L(f)}{\partial w_i} = \sum_n -\delta(y_n f(x_n) < 1) y_n x_n^i \]
现在我们回过头看一下,因为用梯度下降,所以我们可以用一个linear combination来表示\(w\),也就是表示为:\(w^* = \sum_n \alpha_n^* x_n\)。那实际上可以这样表示是因为: \[ w_i^t = w_i^{t-1} - \eta \sum_n -\delta(y_n f(x_n) < 1) y_n x_n^i \] 这个式子如果将\(w\)串成一个vector来看,那么就是 \[ w^t = w^{t-1} - \eta \sum_n -\delta(y_n f(x_n) < 1) y_n x_n \] 那实际上这个迭代到最后,\(w\)就是\(x\)的一个linear combination。这样一来,我们就可以把\(w\)直接表示为\(w = \boldsymbol{X \alpha}\)。那我们因为用的是hinge loss,所以正确分类的sample就不会再提供梯度,所以\(\boldsymbol{\alpha}\)是一个sparse的向量,这个向量我们就叫做support vector。这里要注意一点,如果没有做特殊说明,所有的vector这里都是表示列向量,所以这边的\(\boldsymbol{X}\)的行表示feature,列表示sample。
现在因为我们的模型是linear的,所以\(f(x) = w^{\top} x = \boldsymbol{\alpha}^{\top} \boldsymbol{X}^{\top} x = \sum_n \alpha_n K(x_n, x)\),这样我们就把kernel function带出来了。
kernel function的好处就是,非常方便快速可以做到feature transform。比如说,我们的kernel用的是polynomial,那么我们就是将\(x\)投影到\(\phi(x)\)。比如说我们要做的一个polynomial是将\(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\)变成\(\begin{bmatrix} x_1^2 \\ \sqrt{2} x_1 x_2 \\ x_2^2 \end{bmatrix}\),那么不用kernel function的话,我们需要先做feature transform,把所有的feature变成这样,然后计算。现在因为有了kernel function,所以我们要做的事情就很简单,我们只要做\(\phi(x)\)跟对应的\(\phi(z)\)的inner product就可以了。也就是: \[ \begin{align} K(x, z) &= \phi(x) \cdot \phi(z) = \begin{bmatrix} x_1^2 \\ \sqrt{2} x_1 x_2 \\ x_2^2 \end{bmatrix} \cdot \begin{bmatrix} z_1^2 \\ \sqrt{2} z_1 z_2 \\ z_2^2 \end{bmatrix} \\ &= x_1^2 z_1^2 + 2 x_1 x_2 z_1 z_2 + x_2^2 z_2^2 \\ &= (x_1 z_1 + x_2 z_2)^2 \\ &= (x \cdot z)^2 \end{align} \] 所以有了这个kernel function,我们就可以很快速做到feature transform。那上面这个变化就是做了一个二阶的多项式变化。
那如果我们用的是radial的kernel,实际上我们就做到了无穷多阶的polynomial。怎么说呢?radial的kernel做的事情是\(K(x, z) = \exp(-\frac{1}{2} \|x - z\|_2)\),我们化简一下这个公式: \[ \begin{align} K(x, z) &= \exp(-\frac{1}{2} \|x - z\|_2) \\ &= \exp(-\frac{1}{2} \|x\|_2 -\frac{1}{2} \|z\|_2 + x \cdot z) \\ &= \exp(-\frac{1}{2} \|x\|_2) \exp(-\frac{1}{2} \|z\|_2) \exp(x \cdot z) \\ &= C_x C_z \exp(x \cdot z) \end{align} \] 现在开始表演了,我们得到\(\exp(x \cdot z)\),根据泰勒展开,我们得到的是\(\sum_0^{\infty} \frac{(x \cdot z)^i}{i!}\),这就是一个无穷多维的多项式了,也就意味着,我们将原来的feature映射到了无穷多维的空间中去,而不需要提前做feature transform。不过这里的问题就是,因为维度太高了,一来运算慢,二来很可能过拟合。
最后介绍一个很常见的kernel,就是sigmoid kernel。sigmoid kernel的公式是\(K(x, z) = tanh(x \cdot z)\),那在实作的时候,其实我们的公式是这样的\(K(x_n, x)\),所以我们可以将这个过程看作是一个单层的神经网络,结构如下:
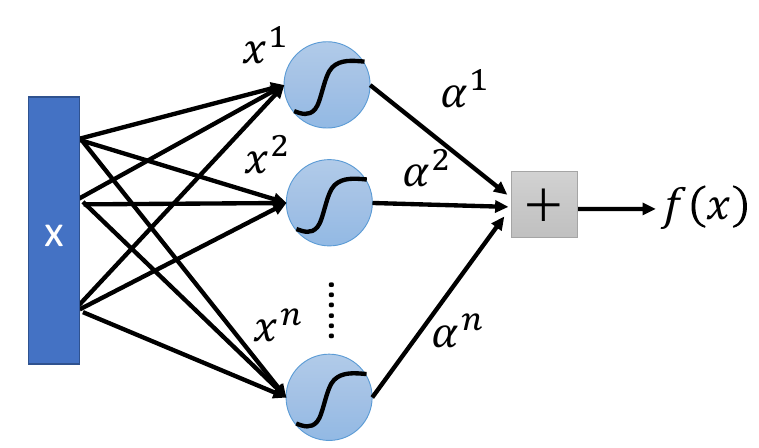
也就是说将每个\(x\)的各个维度的值当做为weight,所以有多少样本就有多少neuron。
