RNN是一种比较复杂的网络结构,每一个layer还会利用上一个layer的一些信息。
比如说,我们要做slot filling的task。我们有两个句子,一个是“arrive Taipei on November 2nd”,另一个是“leave Taipei on November 2nd”。我们可以发现在第一个句子中,Taipei是destination,而第二个句子中Taipei是departure。如果我们不去考虑Taipei前一个词的话,Taipei的vector只有一个,那么同样的vector进来吐出的predict就是一致的。所以我们在做的时候就需要把前一个的结果存起来,在下一个词进来的时候用了参考。
所以这样我们就在neuron中设计一个大脑来存储这个值。所以网络长这样:
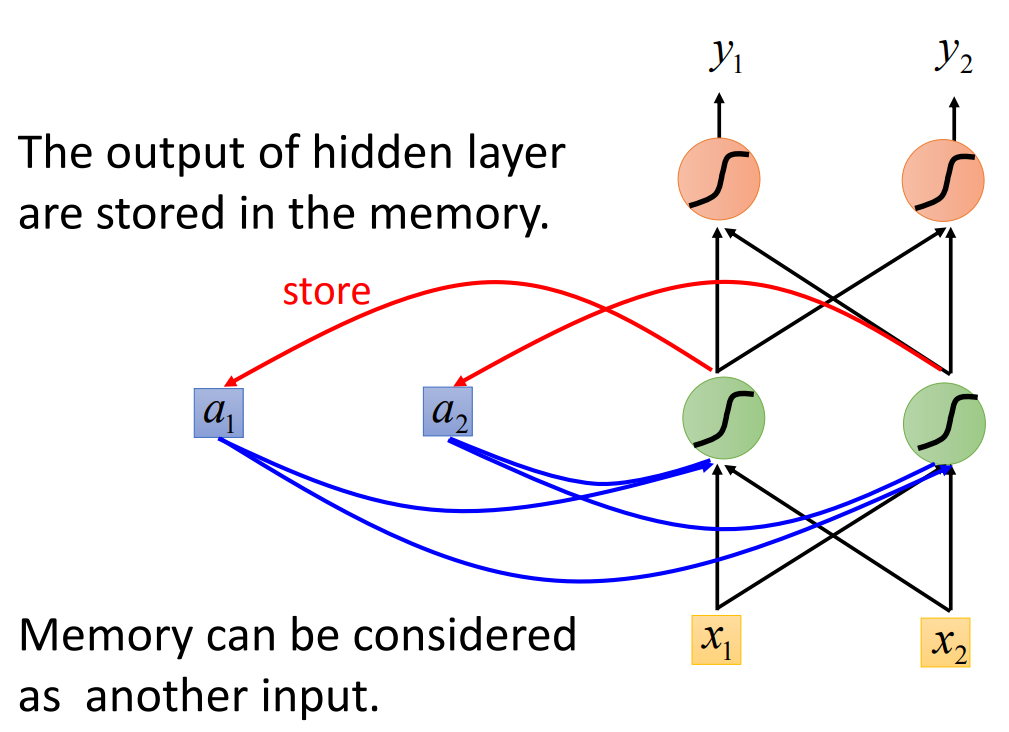
我们用这个网络来举例。假设我们每个weight都是1,每个activation都是linear的。那么我们现在有一个序列\((1, 1),(1, 1),(2, 2)\),那么一开始memory里面的值是\((a_1 = 0, a_2 = 0)\),现在将序列第一个值传入network,我们得到\((x_1 = 1, x_2 = 1)\),因为active function都是linear的,所以经过第一个hidden layer,我们输出的就是\(1 \times a_1 + 1 \times a_2 + 1 \times x_1 + 1 \times x_2\),两个节点一致。所以第一个hidden layer得到\((2, 2)\),同时我们将\((2, 2)\)保存起来,更新一下得到\((a_1 = 2, a_2 = 2)\),output layer是\((4, 4)\),所以得到第一个\((y_1=4, y_2=4)\)。第二个input \((1, 1)\),同样计算一下,hidden layer得到的是\((6, 6)\)和\((a_1 = 6, a_2 = 6)\),output layer是\((12, 12)\)。同理第三个input最后得到的output是\((32, 32)\),所最后得到的三个output序列是\((4, 4), (12, 12), (32, 32)\)。
那么我们可以想一下,如果现在的序列顺序变化一下,结果是否会不一致?如果现在的序列是\((1, 1), (2, 2), (1, 1)\),我们得到的是\((4, 4), (16, 16), (36, 36)\)。结果发生了变化。所以RNN对序列是敏感的,这样的特性就表示,在slot filling的task里面,我们前面的arrive和leave将会影响后面接着的Taipei的结果。
当然RNN也可以是深度的,设计上就是
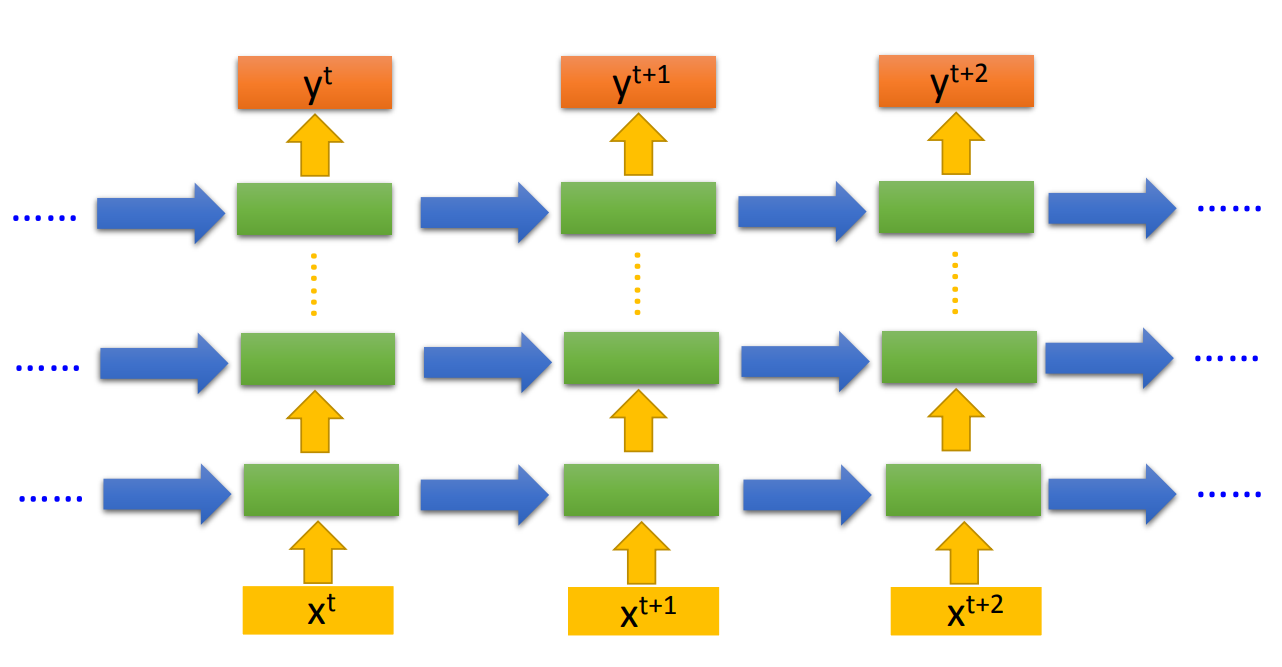
这种深度的设计有两种方法
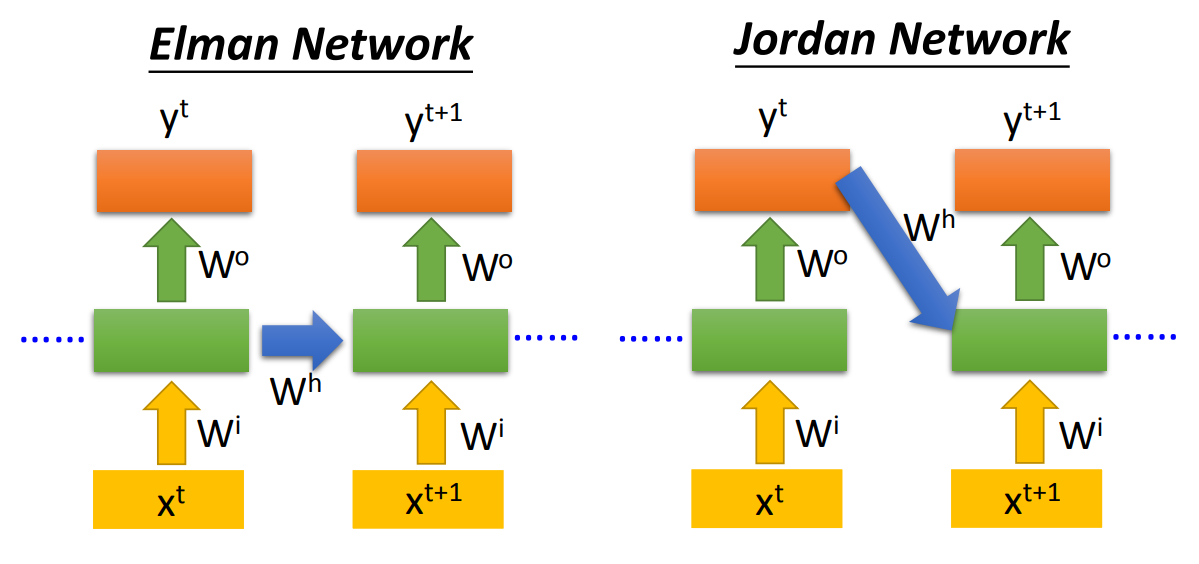
传说Jordan Network一般效果会比较好。另外RNN也可以双向训练:
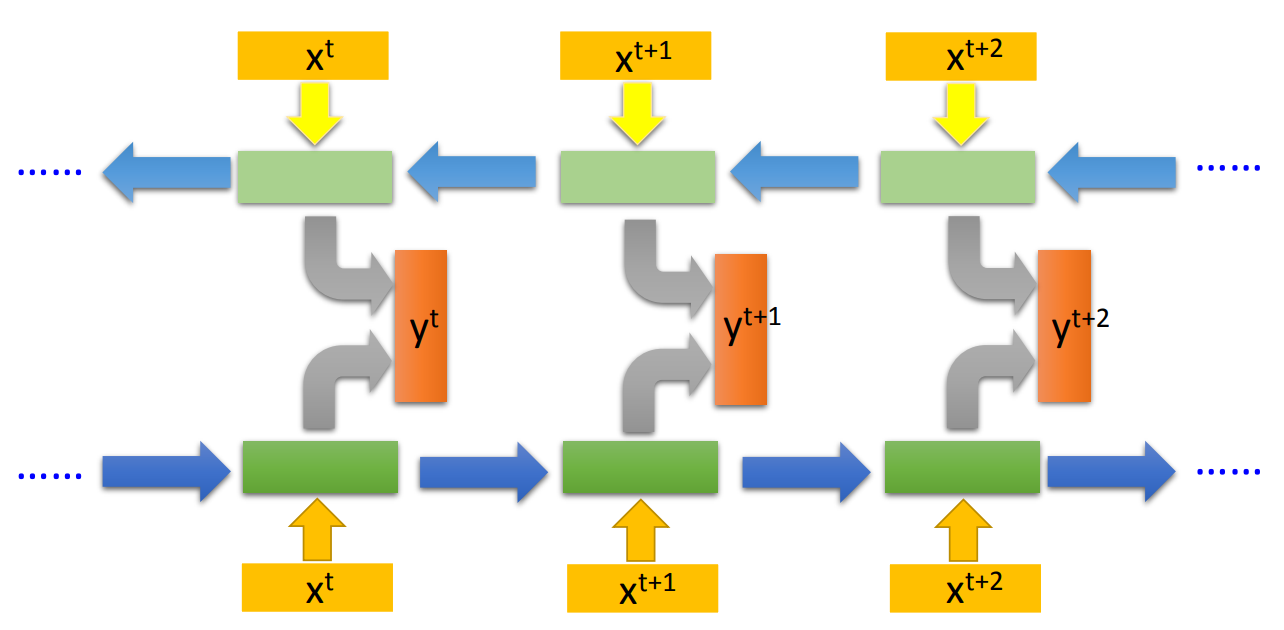
这里也需要注意一下,RNN不是训练好多个NN,而是一个NN用好多遍。所以可以看到RNN里面的这些network的参数都是一致的。
那这个是一个非常原始简单的RNN,每一个输入都会被memory记住。现在RNN的标准做法基本上已经是LSTM。LSTM是一个更加复杂的设计,最简单的设计,每一个neuron都有四个输入,而一般的NN只有一个输入。
LSTM的一个简单结构长这样:
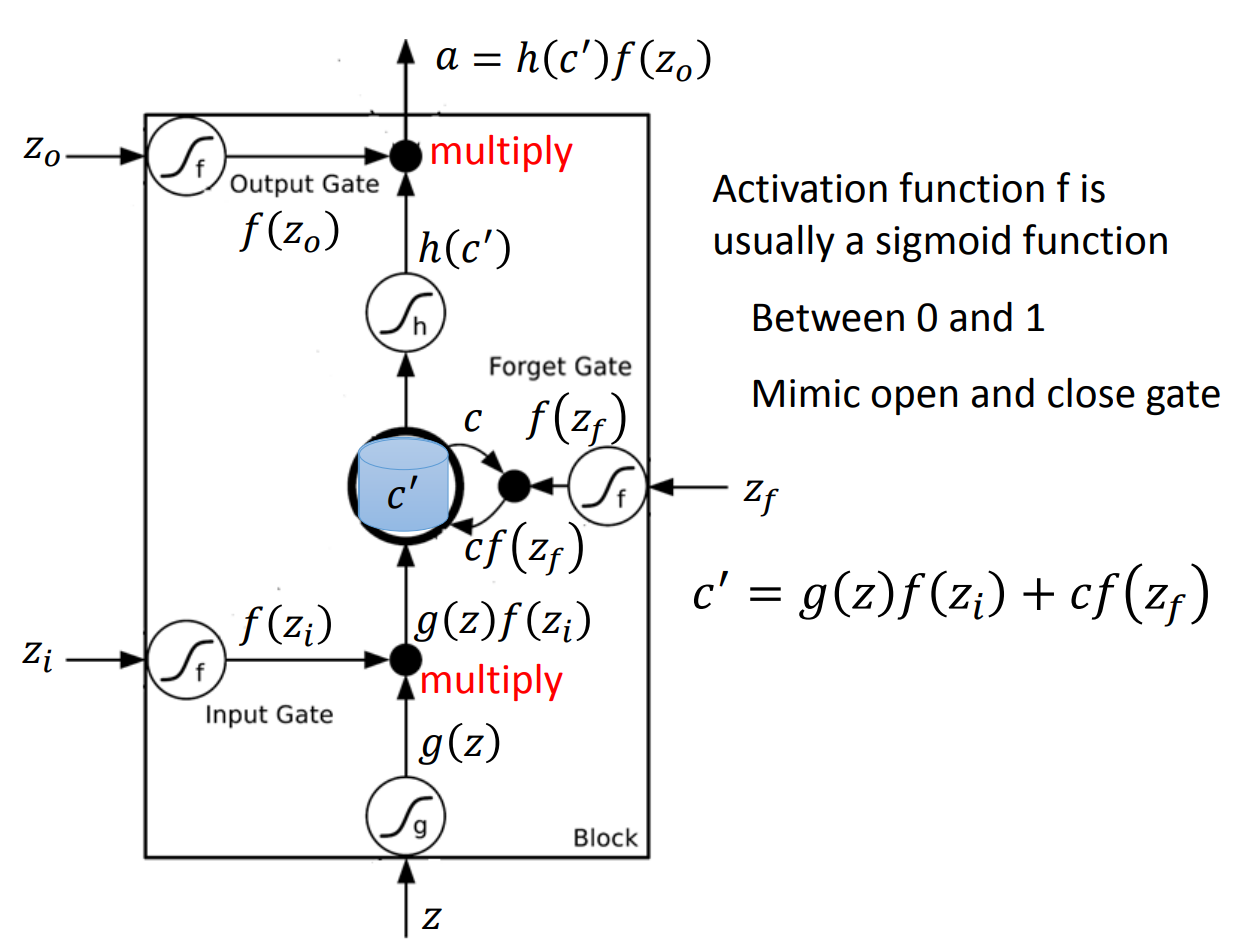
可以看到,一个output受到三个gate的影响,首先是input gate决定一个input是否可以进入memory cell,forget gate决定是否要忘记之前的memory,而output gate决定最后是否可以输出。这样一个非常复杂的neuron。
那么实作上这个neuron是如何工作的呢?假设我们现在有一个最简单的LSTM,每个gate的input都是一样的vector,那么我们这边在做的时候就是每一个input乘以每个gate的matrix,然后通过active function进行计算。这里做一个最简单的人肉LSTM。假设我们有一个序列是:
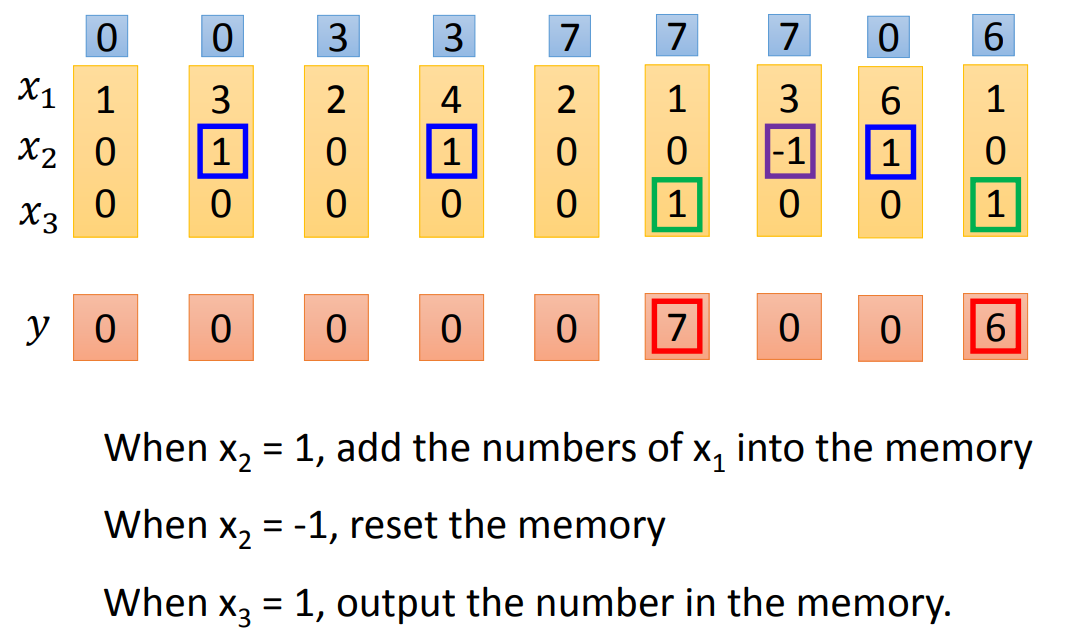
我们希望,当\(x_2 = 1\)的时候,我们将\(x_1\)加入memory中,当\(x_2 = -1\)的时候,memory重置为0,当\(x_3 = 1\)的时候,我们输出结果。
那么我们再假设一个很简单的LSTM,长这样:
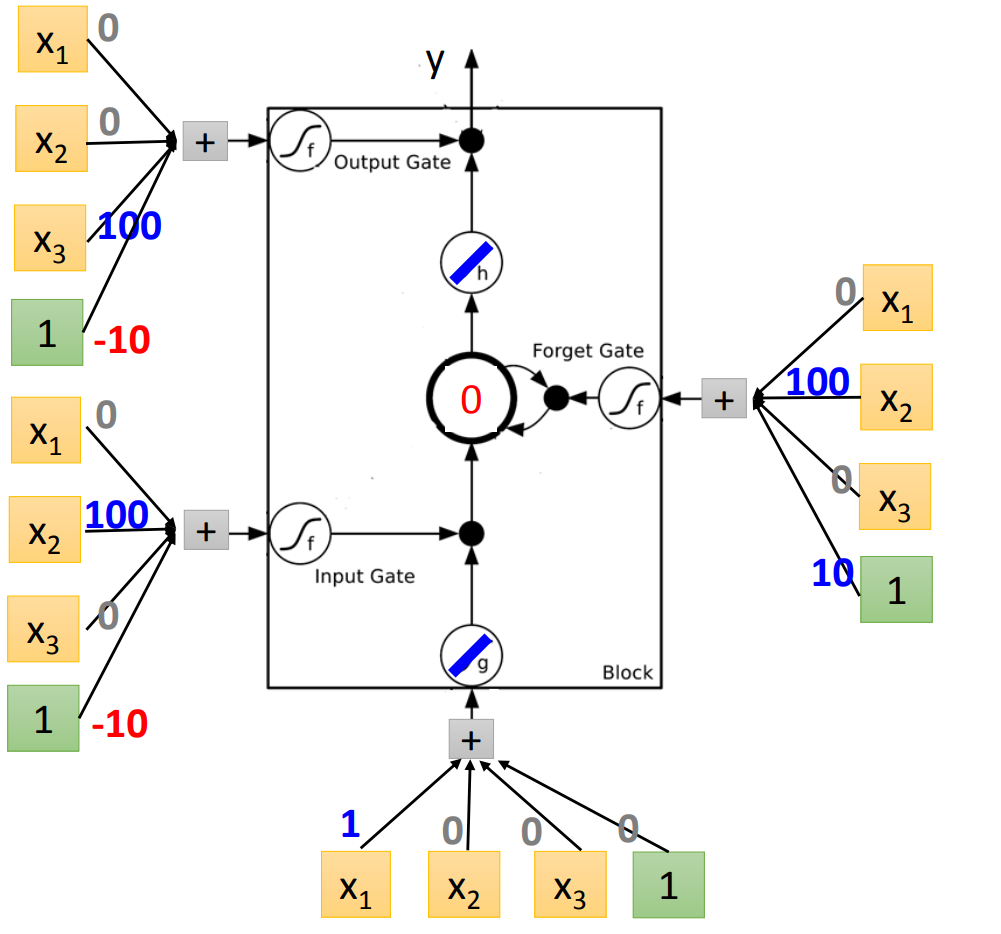
这个cell的input activate function是linear的,memory cell的activate function也是linear的。
那么我们可以将上面的序列简化一下
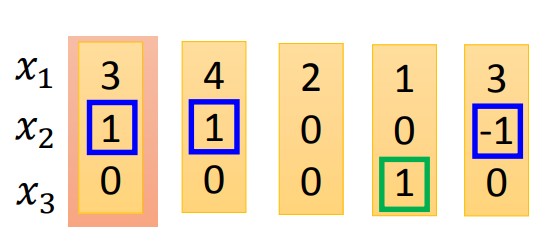
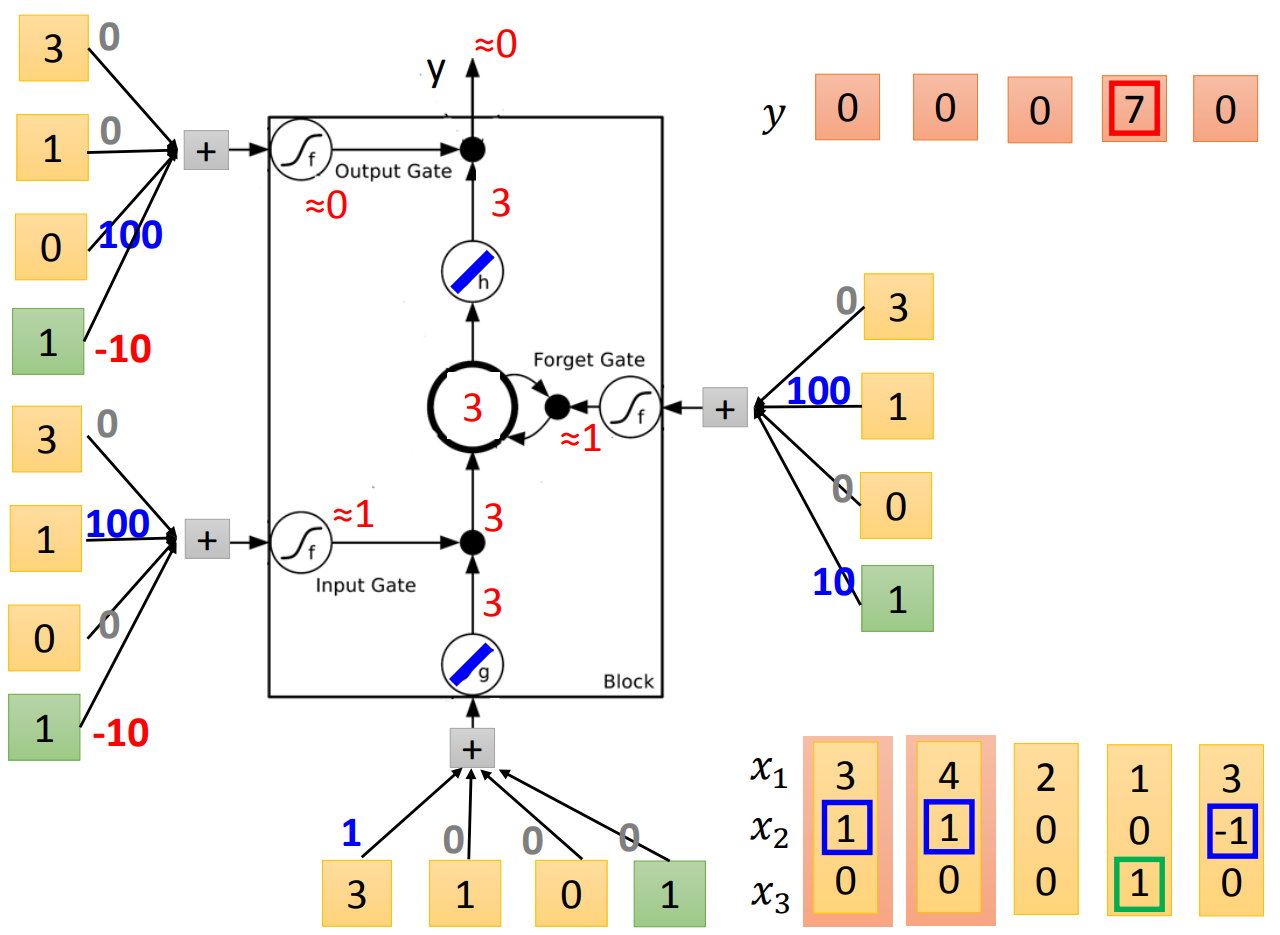
现在,将第一个元素放进来,我们得到是3,input gate部分的结果是90,经过activate function得到的是1,所以允许通过进入memory cell。forget gate这里计算的结果是110,经过activate function是1,所以我们记住这个值(这里要注意,虽然这个gate叫forget gate,但是当取值是1的时候其实是记住,0的时候是遗忘)。然后到output gate这里,output gate计算是-10,activate function输出是0,所以我们不output结果。
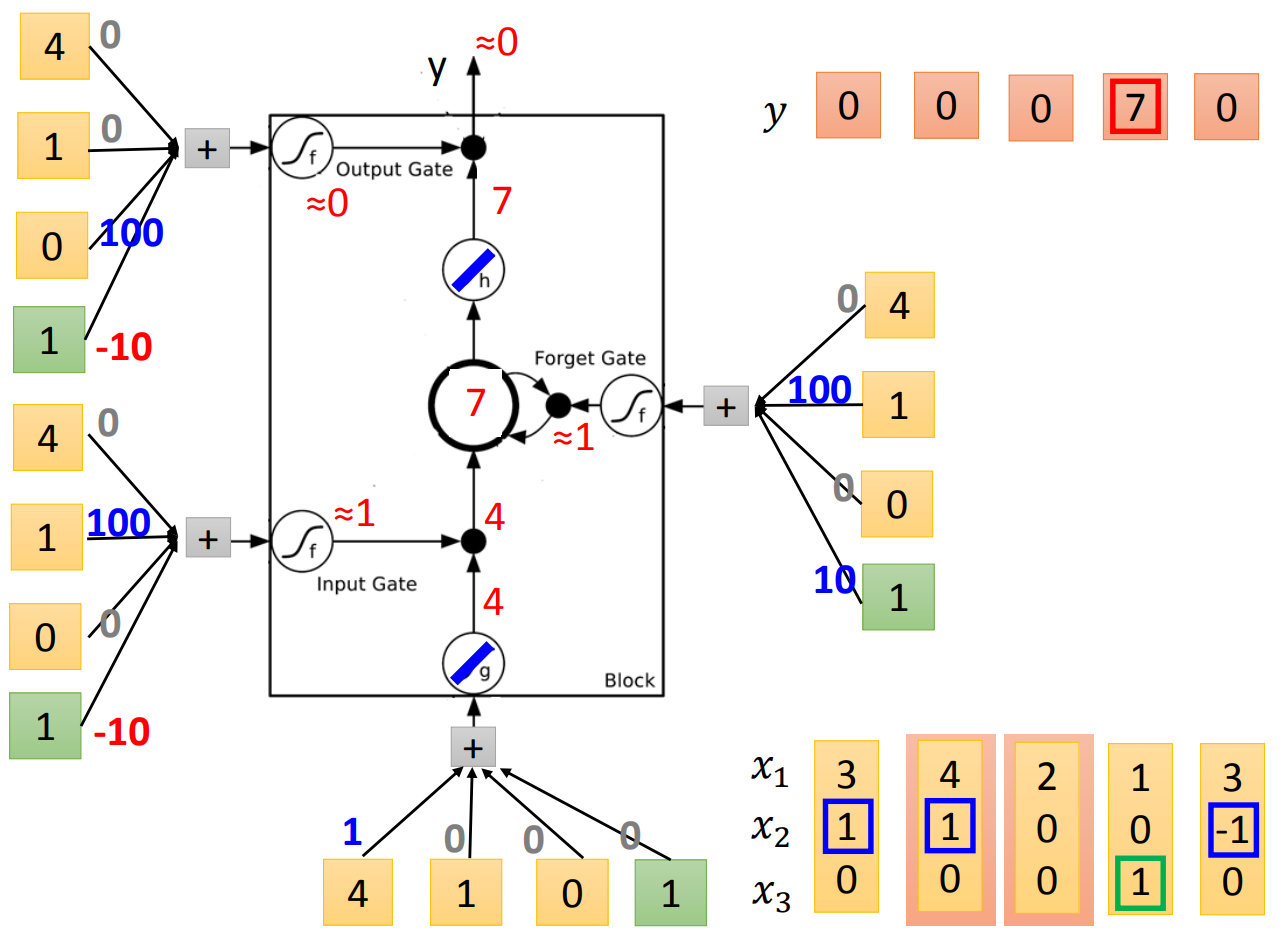
输入下一个元素。直接输入计算是4,经过input gate,得到的是4。因为原来memory cell里面已经存了3,所以这一轮的计算是原来的memory加上新进入的4,得到7。然后output gate依然关闭,所以memory cell还是存7。
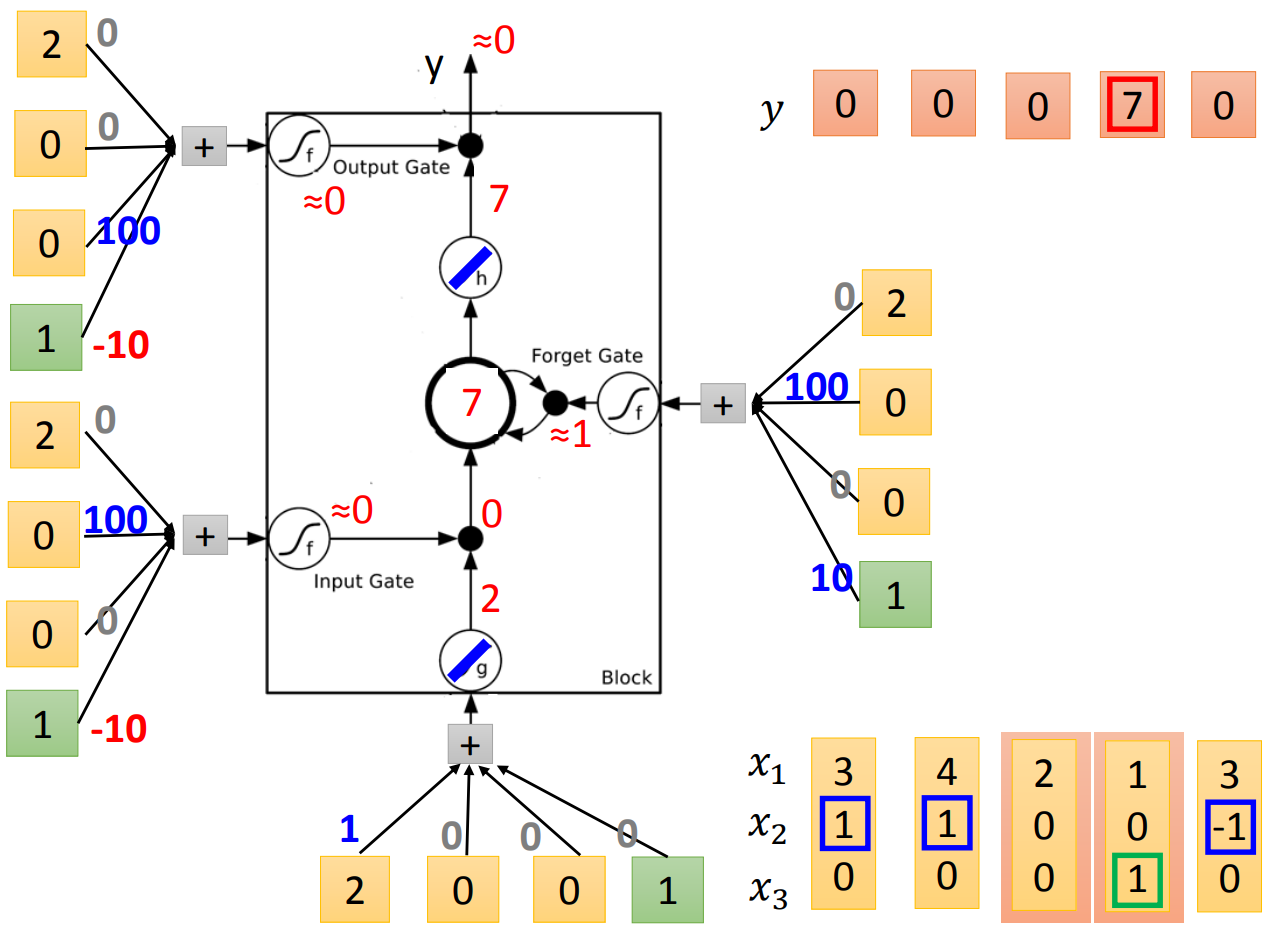
第三个元素类似的计算,发现input gate关闭,所以没法进入memory cell,因此memory cell没有更新。同时output gate关闭,没有输出。
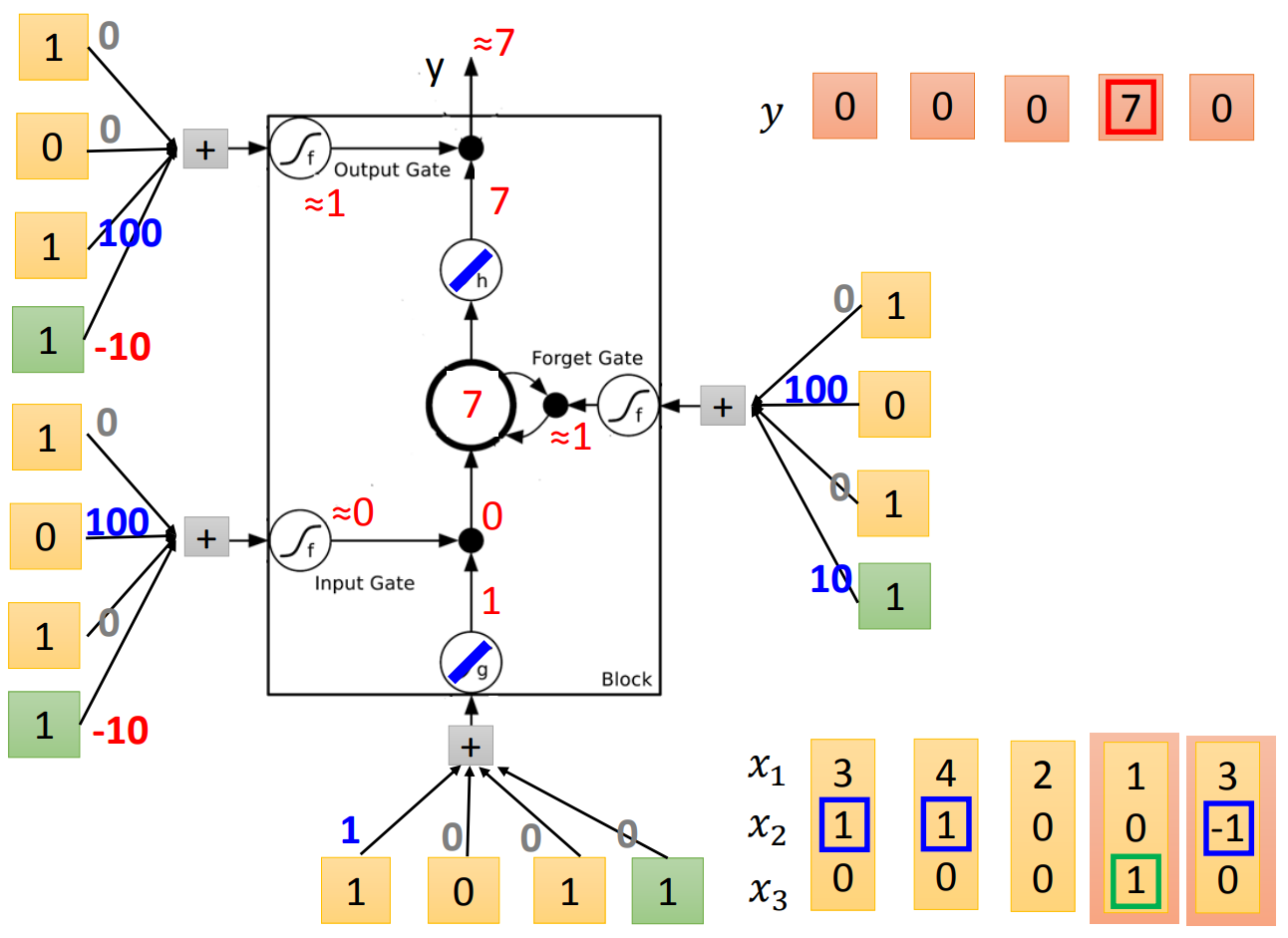
第四个元素进入,input gate关闭,memory cell不更新,但是这时候output gate的activate function得到1,所以开放输出结果。因为之前memory cell里面存放的是7,所以输出7。但是要注意一点,虽然memory cell的值输出了,里面的值并没有被清空,仍然保留着,所以这个时候的memory cell还是7。
最后一个元素进入,input gate关闭,memory cell不更新,这时候,forget gate的activate function得到的是0,所以我们清空记忆,memory cell里面现在是0。output gate仍然关闭,所以没有output。
上面五个过程用图表示如下:
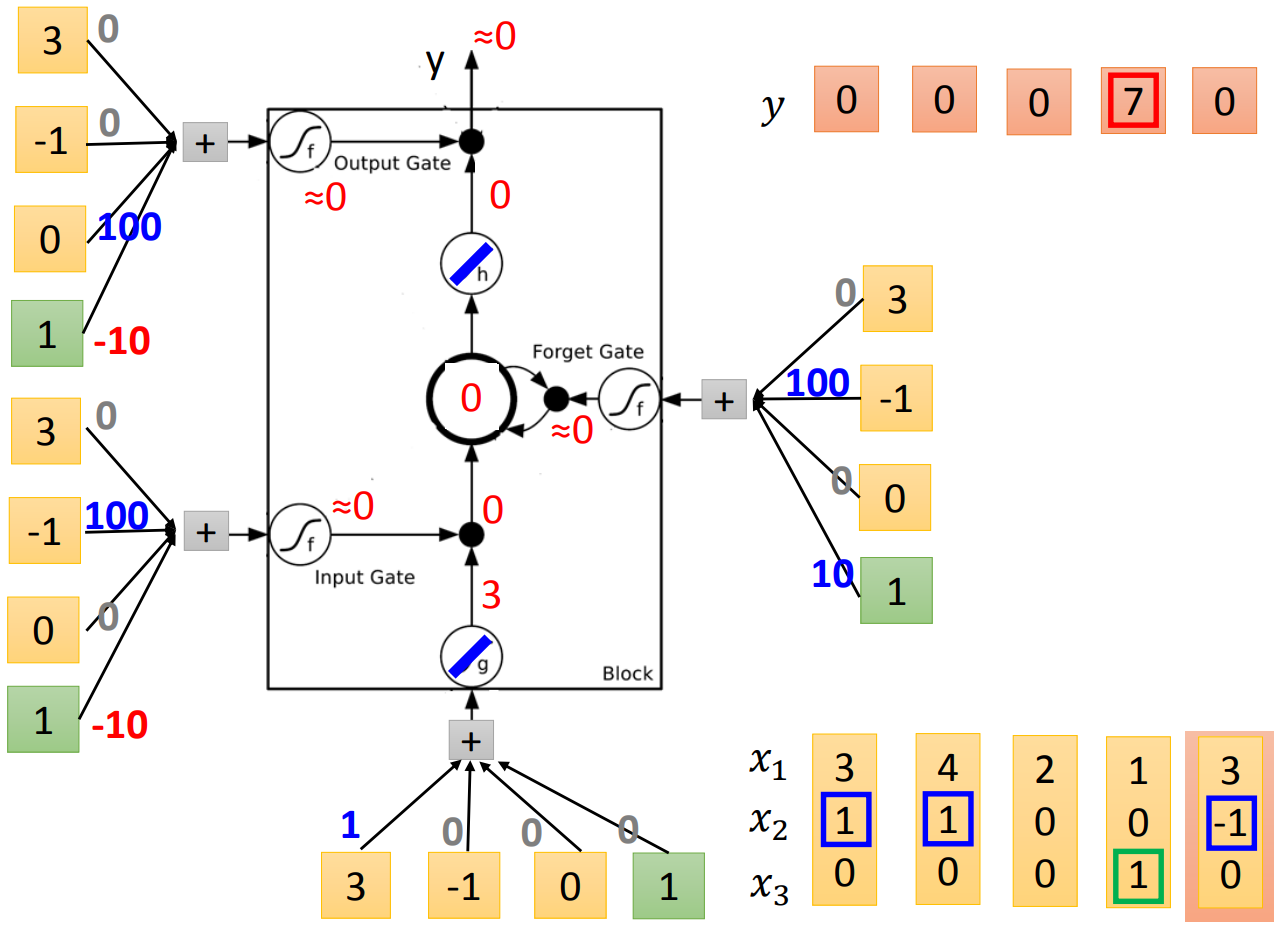
那实作的时候,一个简化的LSTM是:
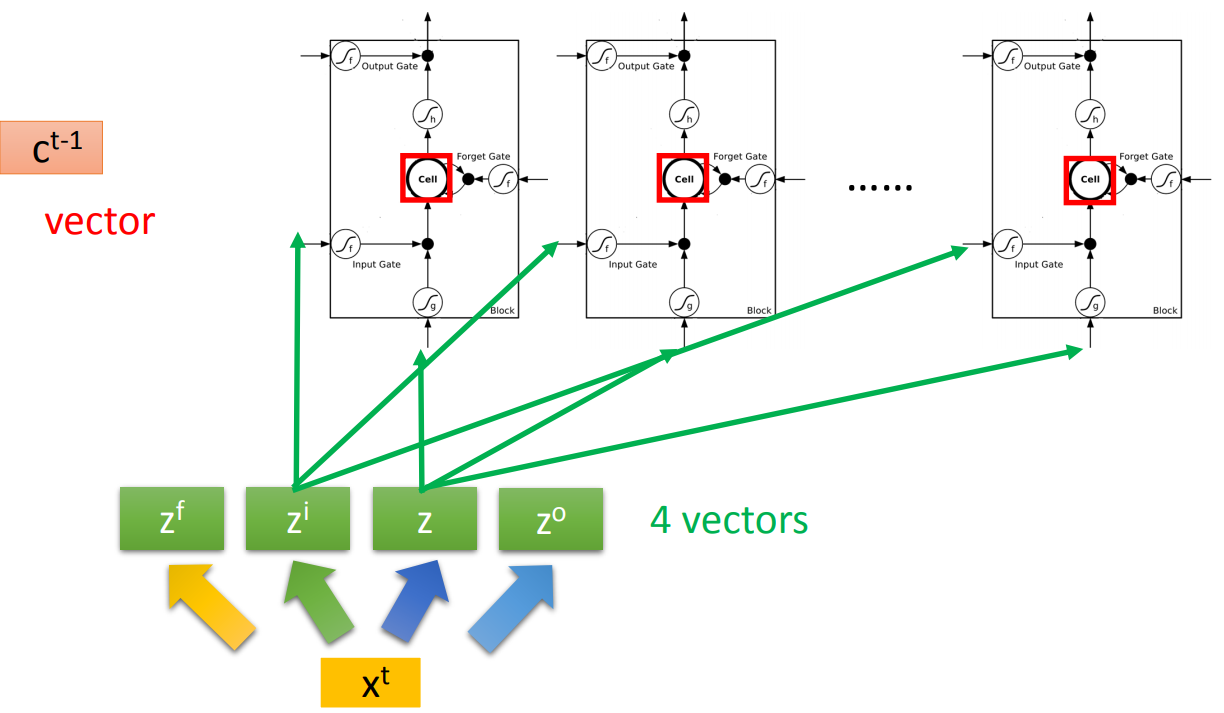
如图中,我们输入一个原始的\(x^t\),会通过四个linear transform变成四个vector,然后每个vector输入到对应的gate。这里要注意的是,转换后的\(z\)有多少个维度,那么我们就需要建立多少个LSTM的cell,同时,每次进入cell训练的只是\(z\)的一个维度。
这是实作上的运算过程:
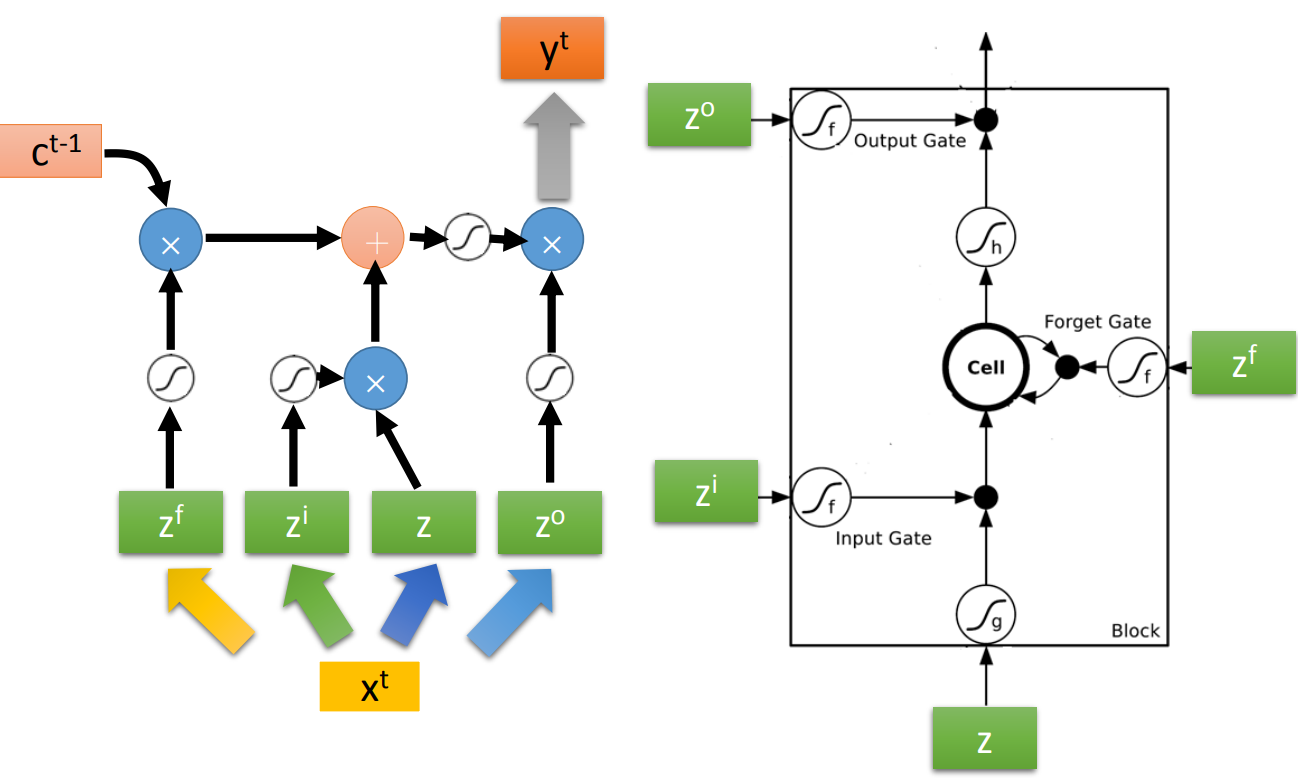
这里的乘不是inner product,是elementwise product。
上面是最simple的LSTM,实际的LSTM如下图:
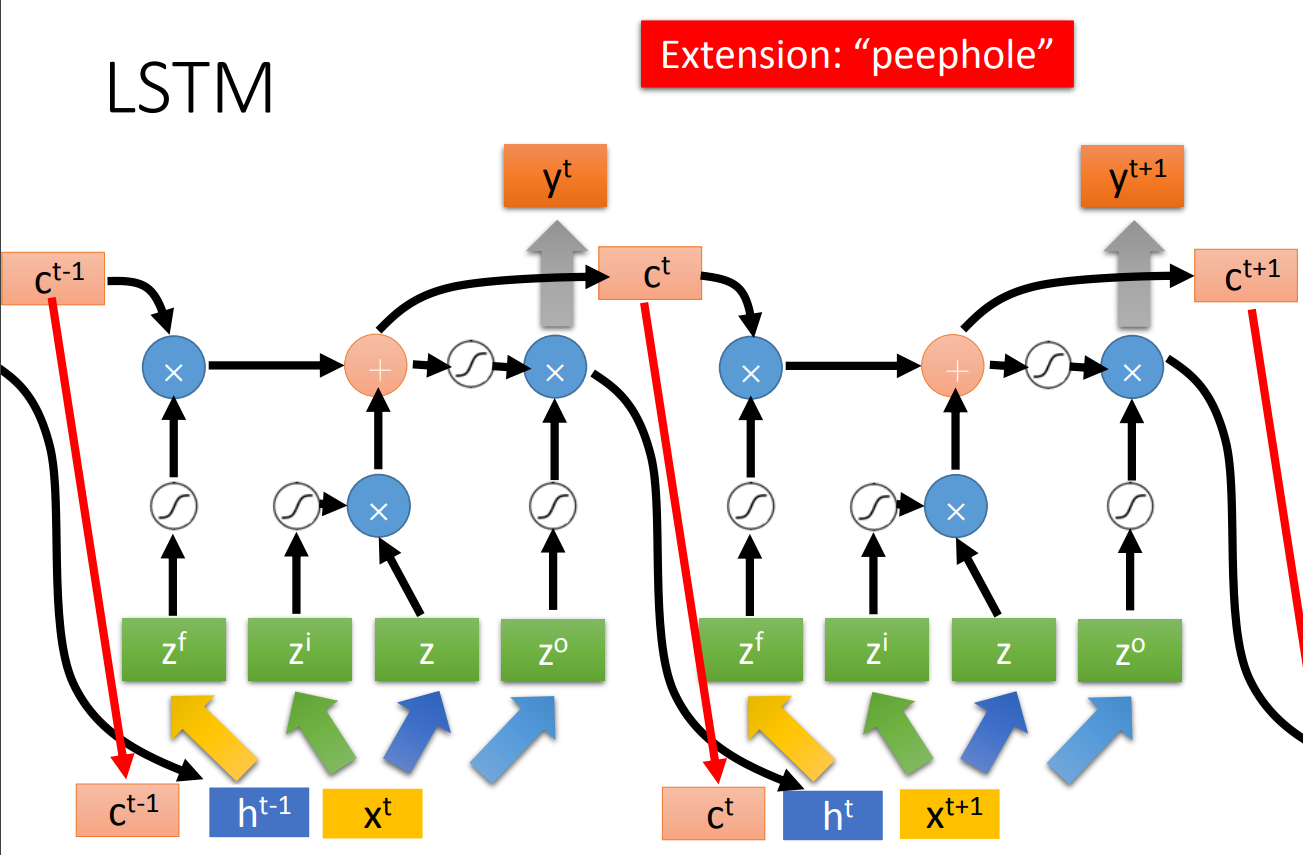
嗯,天书。不过这是现在LSTM的标准做法。
RNN很难训练,因为有个问题就是可能梯度爆炸,有可能梯度消失。我们用一个最简单的模型来体验一下这个问题。假设我们现在的模型是非常simple的RNN,activate function是linear的,如下图:
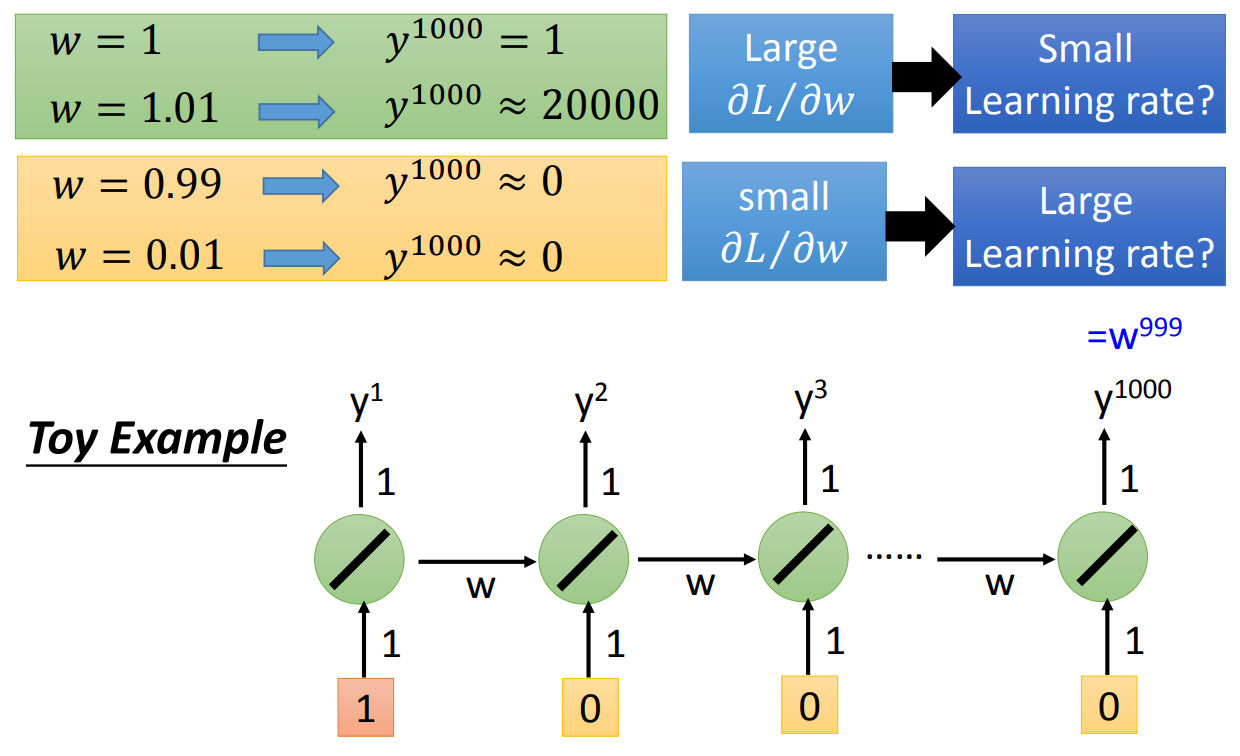
我们可以发现,如果我们有1000个cell,那么我们的weight从1 update到1.01的时候,到了第一千个输出就从原来的1变成了2w,梯度爆炸了。但是当我们weight从1 update到0.99,那么到了第一千个输出就变成了0。更极端一点,如果我们因为之前选择了一个很大的lr,那么我们一步就把weight调到了0.01,我们发现,第一千个输出还是0。所以一般的RNN难以训练是有两个问题的,一个是梯度爆炸,一个是梯度消失。
那么LSTM在实现的时候,因为有了forget gate的存在,只要forget gate长期保持开启,那么很久以前的数据会持续影响后面的数据,所以可以抹消掉梯度消失的问题。另外memory cell里面的值是加起来而不是simple RNN里面直接抹消的,所以这也是能解决梯度消失的问题。
LSTM有个简化加强版叫GRU这个在李老师另一门课有讲,先把坑留着。
