台大李宏毅机器学习作业——梯度下降

机器学习课程的课程作业。嗯，突然发现一直上理论没有实践，机器学习这样一门实践科学怎么能不实践。

课程第一次作业在这里

课程用的是kaggle玩的一个数据，预测PM2.5，不过因为不是班上的学生，所以我没法提交，就不用这个数据了。可以用kaggle上面的练手数据来搞。这里我就用kaggle上面的Pokemon这个数据来练手。反正就是搞着玩的。

课程的要求是自己用梯度下降实现一个线性回归，不能用现成的框架，比如Python必备的sklearn，当然同理也不能用MXNet或者TF这样的重武器了。

用梯度下降来实现的话，其实有一个很简单的，重点就是先实现损失函数和梯度下降。秉持写代码就是先写糙活，再做优化的原则，先开始写一个最直觉的函数。

首先我们先算一下梯度下降的公式。我们用最简单的MSE作为损失函数。那么公式上就是\(MSE = \frac{1}{N} \sum_i(\hat{y}_i - y_i)^2 = \frac{1}{N} \sum_i (\sum_j w_j \cdot x_{i,j} - y_i)^2\)。

那么我们做梯度下降的时候就是求\(\frac{\partial L}{\partial w}\)。出于简单理解考虑，假设我们现在只有一个\(w\)，因为多个\(w\)的话我们假设每个feature是相互独立的，求偏导的时候跟单个求导数没啥差别。那我们现在假设只有一个\(w\)，那么我们现在可以发现一个样本进来的时候，误差是\((w \cdot x - y)^2\)，那么我们的梯度就是\(2(w \cdot x -y) x\)，那我们可以发现，其实\(w \cdot x - y\)就是残差，所以这样一来，我们要实现SGD就很简单了。

def sgd(X, y_true, w, eta=0.1, epoch=10):
    rounds = 0
    while rounds < epoch:
        sum_error = 0
        for i in range(len(X)):
            error = sum(X.iloc[i, :] * w) - y_true[i]
            # 根据梯度更新每个参数
            for j in range(X.shape[1]):
                w[j] -= (1 / X.shape[0]) * eta * error * X.iloc[i, j]
            sum_error += error ** 2
        print('epoch: ' + str(rounds) + '  weight: ' + str(w) + '  total error: ' + str(sum_error))
        rounds += 1
    return(w)

这个地方我在梯度的位置加了一个\(\frac{1}{N}\)的系数，就是为了让learning rate设置的时候稍微大一点而已，调整参数的时候稍微简单一点点。不过原始SGD调learning rate就很麻烦。

Pokemon的数据长这样：

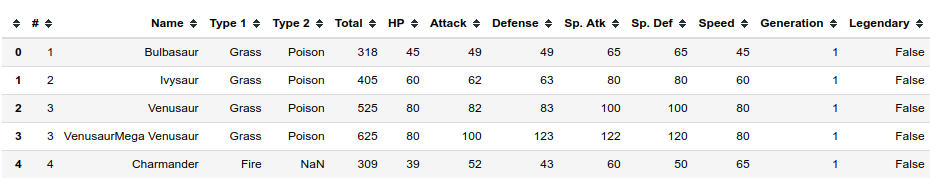
这个数据里面Total等于后面所有属性的和。所以我们可以做这么一个简单的function来试试看我们的梯度下降能不能找出来。

import pandas as pd
import numpy as np
import scipy as sp

data = pd.read_csv('Pokemon.csv')

X = data.loc[:560, ['Total', 'HP', 'Defense', 'Sp. Atk', 'Sp. Def', 'Speed']]
y = np.array(data.loc[:560, 'Attack'])

X['constant'] = 1

def sgd(X, y_true, w, eta=0.1, epoch=10):
    rounds = 0
    while rounds < epoch:
        sum_error = 0
        for i in range(len(X)):
            error = sum(X.iloc[i, :] * w) - y_true[i]
            sum_error += error ** 2
            for j in range(X.shape[1]):
                w[j] -= (1 / X.shape[0]) * eta * error * X.iloc[i, j]
        rounds += 1
        print('epoch: ' + str(rounds) + '  weight: ' + str(w) + '   error: ' + str(sum_error))
    return(w)

w = np.random.rand(X.shape[1])
print(w)
sgd(X, y, w, 0.0001, 1000)

这里我在最后加了一个常数进来，就是一般书上的bias，参数是\(w_0\)。如果顺利的话，我们应该看到的是\(w = [1, -1, -1, -1, -1, -1, 0]\)或者是这附近的权重向量。

训练1000轮之后的效果是：

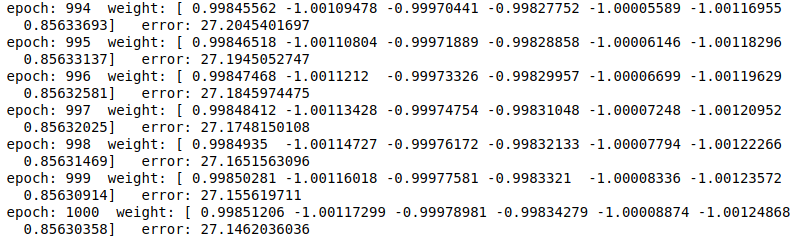
可以看到最后的weight其实还是挺接近正确答案的，只是常数项没有被消掉。那我们试试看训练5000轮的效果。

这一次看上去比上一次的好很多。那么是不是真的越多就一定越好呢？回顾了一下自己的代码，发现这里有一个问题，我的\(w\)是随机initialize的，那很可能这个也有影响。所以重新做个实验。我们把随机初始化改成初始全部为0，分别跑1000次和5000次，看看是什么效果。（PS：这里提醒一下，因为numpy恶心的一点，所以我们要用float的类型而不能用int，也就是0要表示为0.。否则的话weight会一直保持在0。）

1000个epoch的效果：

5000个epoch的效果：

我们可以看到的是，其实5000轮没比1000轮好出多少。但是相比之前在0-1之间随机初始化的要好出不少，1000轮的结果就比上一次5000轮的好。这也是为什么很多时候机器学习的权重初始化会设计在0附近，或者干脆全部设计为0。

但是这里有个问题，明明简单线性回归的损失函数是有一个最优解的，而且只有一个最优解，那为什么我们就到不了呢？其实也很好理解，因为快到碗底的时候速度会非常非常的慢，这里的梯度我们类比为速度，那么分解到水平方向的速度就很小。所以这就会有一个非常尴尬的事情，就是说实践上，别说是全局最优了，我们连局部最优都到不了。如果损失函数再复杂一点，我们连saddle point都到不了。那如果我们把步长设得很大呢？如果这样，我们很可能一步跨到对面山上，然后就收敛不了了。

那现在如果我们做个regularization会怎么样呢？我们这里实现一个\(L_2\)，那么其实我们这里的梯度下降就变成了\(\frac{2}{N}(w \cdot x -y) x + 2 \lambda w\)，那么我们可以把梯度下降改一下。

def sgd(X, y_true, w, eta=0.1, epoch=10, penalty=0.1):
    rounds = 0
    while rounds < epoch:
        sum_error = 0
        for i in range(len(X)):
            error = sum(X.iloc[i, :] * w) - y_true[i]
            sum_error += error ** 2
            for j in range(X.shape[1]):
                w[j] -= (1 / X.shape[0]) * eta * error * X.iloc[i, j] + penalty * w[j]
        rounds += 1
        print('epoch: ' + str(rounds) + '  weight: ' + str(w) + '   error: ' + str(sum_error))
    return(w)

那这里要注意一点，就是说如果我们的penalty设的太大，模型会趋向于保守，换句话说就是权重的更新会比较小，收敛起来会非常非常非常慢。上面的梯度下降里面我们把常数项也做了regularization，那weight初始化全是0，迭代1000轮的效果如下：

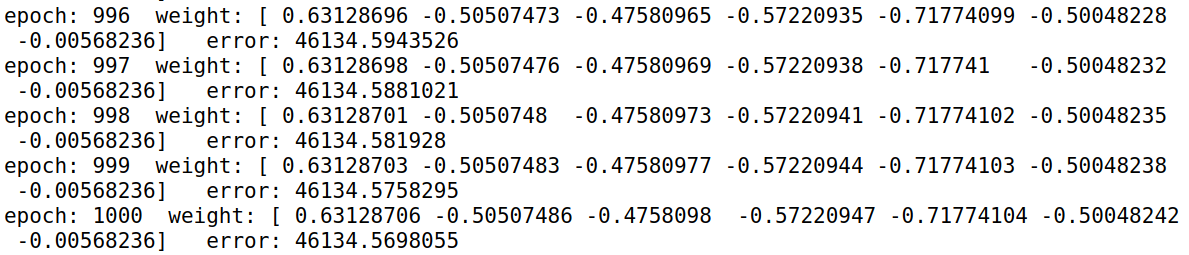
可以看到的是，这边的weight收敛非常慢。现在我们再试一下不对常数项做regularization会怎么样：

可以看到的是，其实常数项这边加不加regularization对其他的参数影响是不太大的。所以本质上我们没有必要去对bias做regularization。

既然SGD都实现了，我们干脆把adagrad也实现一下。adagrad其实很容易做，就是在learning rate那里做动作，加上一个系数。所以我们的梯度下降就可以写作：

def adagrad(X, y_true, w, eta=0.1, epoch=10):
    rounds = 0
    while rounds < epoch:
        sum_error = 0
        grad = np.array([0., 0., 0., 0., 0., 0., 0.])
        for i in range(len(X)):
            error = sum(X.iloc[i, :] * w) - y_true[i]
            sum_error += error ** 2
            for j in range(X.shape[1]):
                grad[j] += (error * X.iloc[i, j]) ** 2
                w[j] -= (1 / X.shape[0]) * (eta / np.sqrt(grad[j])) * error * X.iloc[i, j]
        rounds += 1
        print('epoch: ' + str(rounds) + '  weight: ' + str(w) + '   error: ' + str(sum_error))
    return(w)

利用adagrad，我们可以一开始就把eta设大一点，我这里设到10，然后迭代100轮就得到了：

使用adagrad这样的算法好处就是learning rate比较好调，一开始给一个大一点的，然后迭代次数多一点就好了。原始SGD其实learning rate不是那么好调的。

框架有了，其实后面要试增加样本量，去掉常数项啥的就很方便了。