无监督学习的neighbor embedding和deep auto-encoder部分。
neighbor embedding
近邻嵌入其实在做的事情就是manifold,白话一点说就是把高维的数据强行压缩到低维空间中。
locally linear embedding
这个模型一开始假设,每一个\(x_i\)都可以是\(x_j\)的linear combination。所以这样就有了一个假设,我们在原始的数据空间中,我们有这样需要优化的函数\(\sum_i||x_i - \sum_j w_{i,j} x_j||_2\)。我们希望这个函数越小越好。那相应的,当我们将数据映射到一个新的空间中的时候,我们得到\(\{z_i\}\),我们同样希望,在这个空间中,我们能够保留原来数据空间中的特性,也就是原来接近的数据点在这个空间中还是接近的,而且两者之间的关系不变。所以相应的,在这个新的空间中,我们又有一个可以优化的函数\(\sum_i||z_i - \sum_j w_{i,j} z_j||_2\)。
那么我们做的事情就是,用第一个优化的函数找\(w_{ij}\),然后固定住\(w_{ij}\),找一组\(\{ z_i \}\)使得第二个优化函数最小。
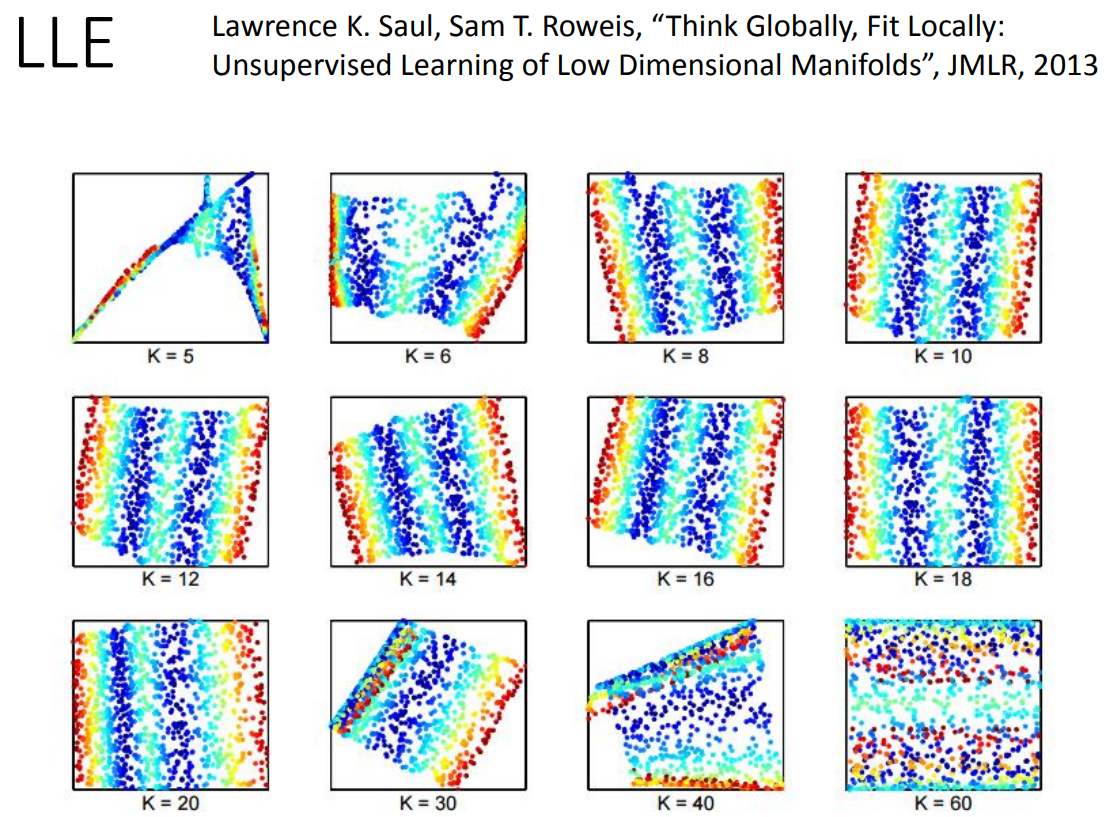
那用LLE一般来说,邻居选太多或者选太少效果都不会太好。如下图:
laplacian eigenmaps
拉普拉斯特征映射用的是graph-based的方法。那跟之前semi-supervised learning就用过这种方法。在半监督学习的时候,我们的loss function是被设计为交叉熵加上一个相似度。但是在有监督学习的时候,我们有labeled data,unsupervised learning是没有labeled data的,因此,我们的函数就设计为\(S = \frac{1}{2} \sum_{i,j} w_{ij}(z_i - z_j)^2\)。
那这里有一个问题,如果不加限制的话,我们一开始就将原来所有的点都映射到新空间中的一个点上,那不就使得这个函数最小了吗?所以这里需要加上一定的限制。假设我们新的空间上有\(M\)个维度,我们希望在新的空间上,\(\text{Span} \{z_1, z_2, \dots, z_N \} = R^M\)。白话一点讲就是我们新空间上的数据摊开后,可以铺满新的空间。
t-SNE
t-SNE全称是T-distributed Stochastic Neighbor Embedding。
那上面两种方法的缺点就是,这两种方法可以找到接近的点,也就是说他们可以保留原来相近点的信息,但是无法保持原来很远的两点的信息。比如这两个算法在mnist上面做降维的时候会得到每一个类别的图像都聚集在一起,但是每一个类别也都堆叠在一起。

那t-SNE比较强大的地方就是可以同时保留相近点的信息,也能保留两个远的点的信息,同时可以将这种gap放大。
那t-SNE的设计就是,在原来的空间上,我们定一个概率:\(P(x_j | x_i) = \frac{S(x_i, x_j)}{\sum_{k \ne l} S(x_k, x_l)}\)。在新的空间上面我们也定义一个概率:\(Q(z_j | z_i) = \frac{S'(z_i, z_j)}{\sum_{k \ne l} S'(z_k, z_l)}\)。这里我们可以发现,t-SNE一个很不一样的地方就是,两个空间上计算similarity的函数可以不一样。
然后我们要做的事情就是,我们尽可能让原始空间上的分布和新空间上的分布尽可能相似,那用KL divergence,也就是相对熵来计算(默默觉得信息论也得看起来的节奏)。 \[ L = \sum_i KL(P(*|x_i) || Q(*|z_i)) = \sum_i \sum_j P(x_j | x_i) \log(\frac{P(x_j|x_i)}{Q(z_j|z_i)}) \]
那因为这边用的是probability,所以我们就可以更改我们的similarity function。那t-SNE选用的similarity函数分别是,在原空间上\(S(x_i, x_j) = \exp(-||x_i - x_j||_2)\),在新空间上\(S'(z_i, z_j) = \frac{1}{1+||z_i - z_j||_2}\)。那效果是这样的:
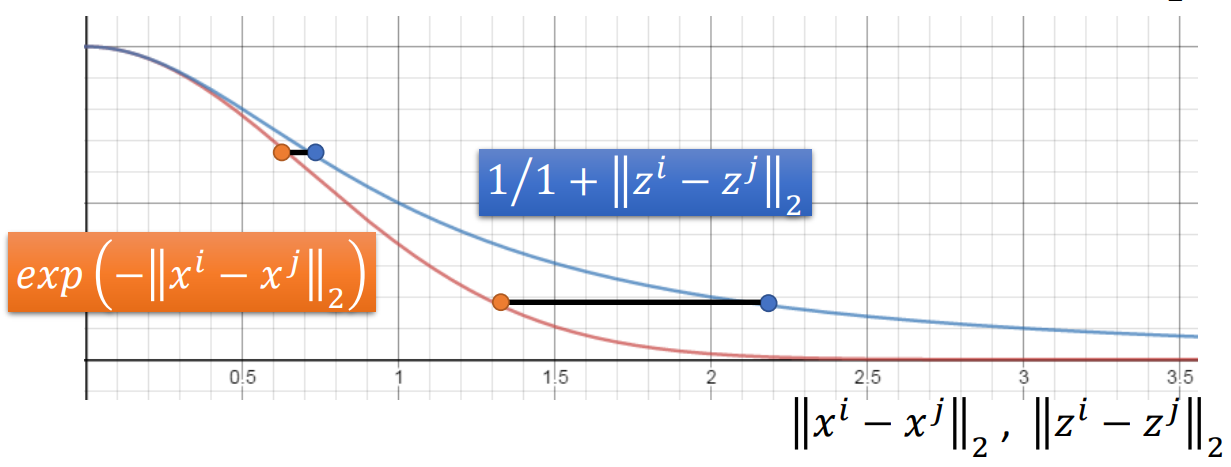
也就是做到原来近的更近,原来远的更远。目前高位数据可视化最好的方案就是t-SNE。
deep auto-encoder
深度自编码模型其实在某种程度上而言,跟PCA非常相似。我们回顾一下PCA的过程,PCA本身就可以看做是一个加密解密的过程,如果用神经网络的方式来表现,那就是input layer encoding到一个hidden layer,我们叫做Bottleneck layer。因为在整个网络结构中就是最窄的位置,就像是瓶颈。然后从这个hidden layer还原。所以整个PCA的结构就可以用神经网络的结构表示为:
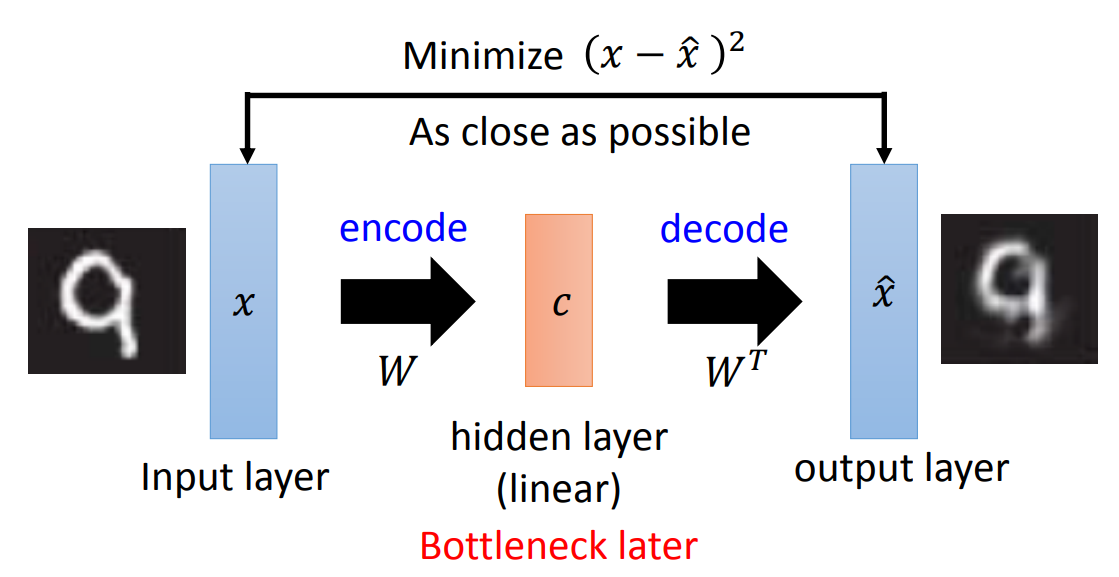
那这样表示的PCA优化的目标就是之前讲到的用最小误差来做。那实际上如果看深度学习圣经的话,书里面用的就是这个方法来求的。
所以我们就可以从PCA很自然引导到deep auto-encoder。在结构上看,deep auto-encoder就是在bottleneck layer前面加好几个hidden layer。结构大致如下:
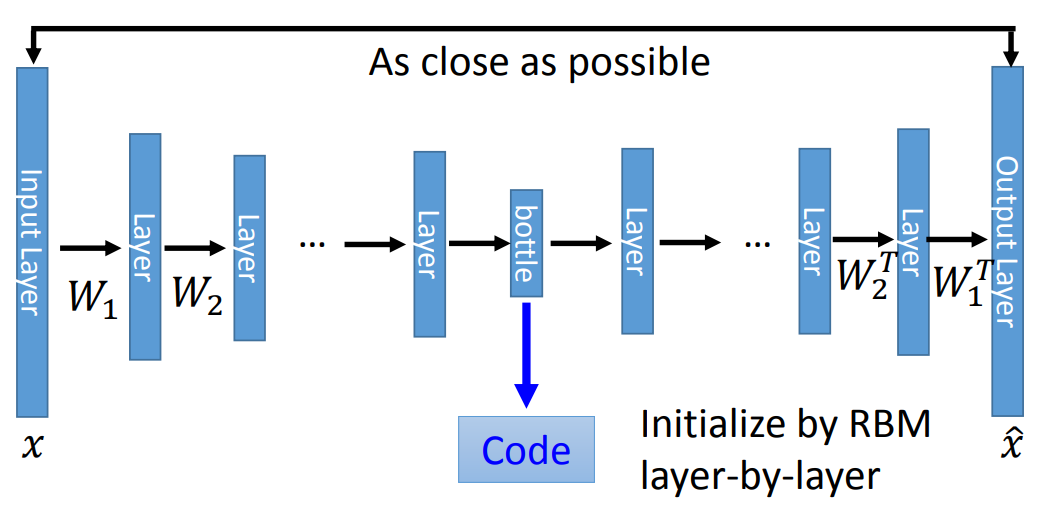
那这里需要注意一点,那就是deep auto-encoder已经不需要RBM来做initialize了。另外这几层layer之间的weight也没必要保证是之前的transpose,因为这样的限制在早期是为了加速训练,减少需要学习的参数。
deep auto-encoder的效果相对会比PCA更好一点,因为PCA是linear的转换,而deep auto-encoder是非线性的变化,所以效果上会更好一点。
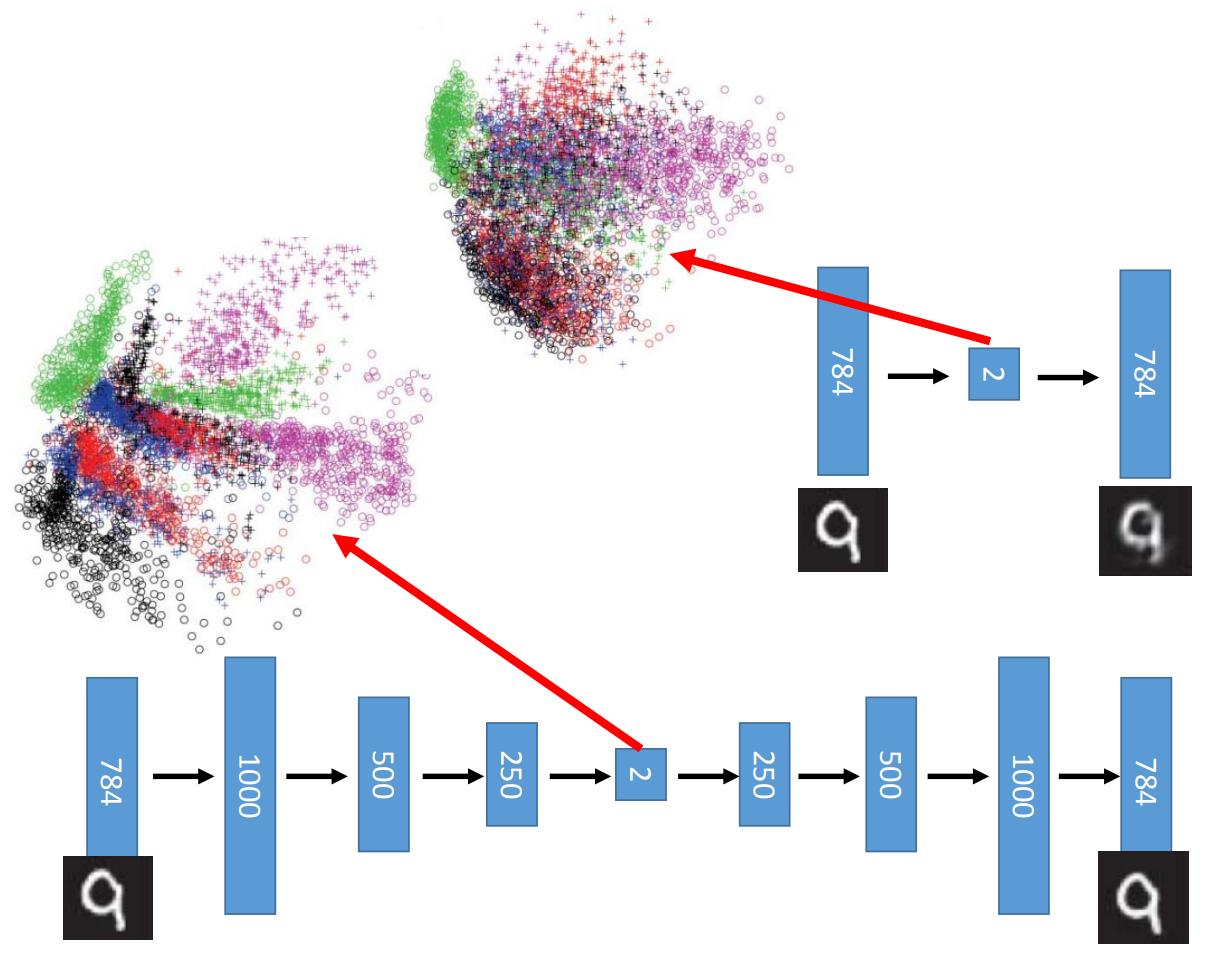
那deep auto-encoder在训练的时候要注意的事情就是,我们一定是要有bottleneck layer的,因为如果我们把每一个hidden layer都设计得比input layer大,那很有可能machine学到的就是直接复制一份input layer出来,这样input跟output的误差就最小了。
那所以如果我们不放bottleneck layer的话,就一定要在input中增加一些noise。
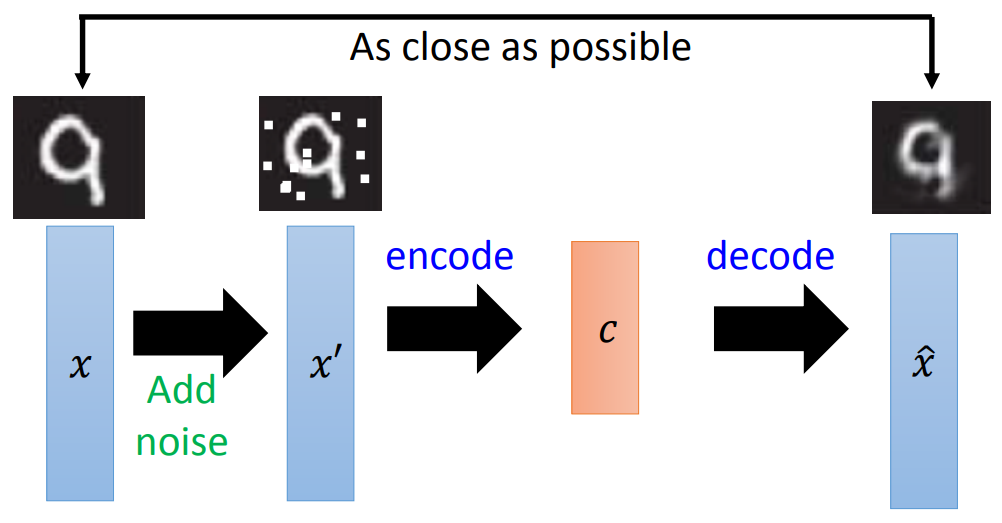
加noise这个事情,其实不管怎么训练deep auto-encoder都可以放,只是说如果没有降维的动作,那一般在实践上是一定要放的。放多少就看缘分吧。后面讲VAE会让模型自己学这个noise。
那模型的训练也就是反向传播,用梯度下降的方法来求。万能的梯度下降。
