无监督学习——clustering & PCA,主要介绍了PCA,顺带讲了一些clustering。
无监督学习课里被分为clustering,dimension reduction,和generate。
clustering是关注在样本方向上的,一般在数据里面就是行方向上的。dimension reduction是对feature的降维,也就是在列方向上的收缩。
clustering
clustering其实是无监督算法的一个大类,比较常用的是算法有层次聚类和k-means。
k-means是一种非常简单的算法,就是一开始先随机选择一些k个初始点,然后计算每一个点离这k个点的距离,选择最近的一个点合并为一类。然后取这k个类的中心点作为新的中心点,再更新一次,直到中心点不再移动为止。
k-means算法是非常简单的算法,后面有了很多新的玩法,现在大部分框架最常用的其实是k-means++,是对初始点选择的一些优化的k-means算法。后面其他玩法还有加核函数,做半监督啥的。其实这样的一些做法都是让算法更稳健一点,但是其实k-means最麻烦的地方是对k的选择。
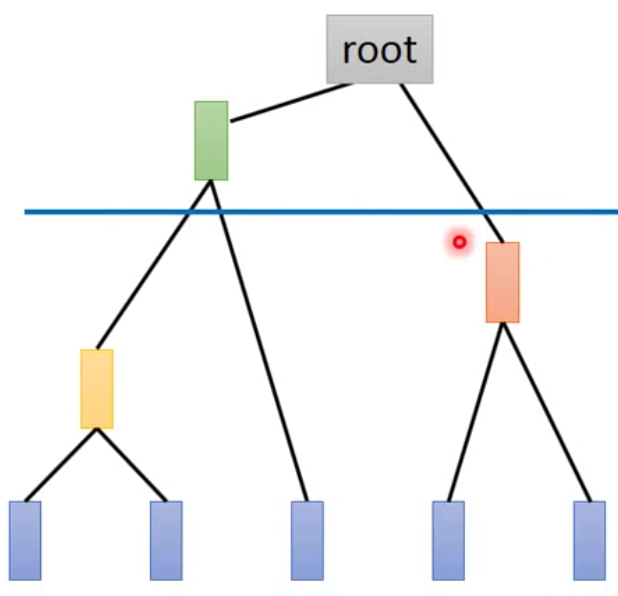
那除了k-means以外,还有一种算法就是层次聚类(HAC),层次聚类就是一开始就计算每个sample两两之间的距离,然后将最近的几个点合并起来,一直合并到只剩下一类。看上去就像是一棵树。那最后我们只要决定在一个什么样的阈值下,将数据分成几类。示意图如下:
PCA
降维的方法有很多种,最简单粗暴的方法就是drop feature。那实际上在回归中就有这样的算法来做这样的事情。比如forward,backward,还有stepwise。这些都是直接drop一些feature的方法。
另外一种常用的方法就是PCA。PCA实际上是对原来的数据进行一次线性转换,映射到新的坐标空间中。它能起到降维的效果是,我们只需要少量的坐标,就可以最大程度上还原数据。
PCA的数学解法有很多种角度,一种是最大方差法,一种是投影再恢复的最小误差法,还有一种是根据SVD求解。鉴于自己忘到很捉急的线代水平,这里就找一种我能理解的解法推算一下好了。(默默滚去补线代)
这里我们考虑最大方差法,需要使用拉格朗日乘子来求解(就是视频里面的Lagrange multiplier)。我们这里假设所有的向量默认都是列向量。下面开始证明:
假设我们有\(n\)个维度\(\{x_1, x_2, \dots, x_n \}\),每个列向量有\(m\)个元素。我们对这些样本做一个中心化的动作,就是每一行的元素减去各自行的均值,我们可以表示为\(\{x_1 - \bar{x_1}, x_2 - \bar{x_2}, \dots, x_n - \bar{x_n} \}\)。做中心化的目的就是使得我变化后的矩阵每一行均值为0,这样算后面的协方差矩阵会更好算一点。
算协方差矩阵之前,我们可以看一下如何计算一维的方差。对于包含\(m\)个元素的一维向量\(a\),我们可以算\(Var(a) = \frac{1}{m} \sum_i^m(a_i - \bar a)^2\),如果按照上面说的都减掉均值的话,我们就可以得到\(\bar a = 0\),因此我们可以让方差简化为\(Var(a') = \frac{1}{m} \sum_i^m (a')^2\),因为向量点内积可以表示为向量的转置乘向量,所以上式又可以改写为\(Var(a') = \frac{1}{m} a'^{\top} a'\)。
那现在我们知道,多维数据我计算的是协方差,所以同样减掉均值以后,我们的协方差也可以化简到各个维度的内积。所以我们可以把协方差求出来\(Cov(a, b) = \frac{1}{m} \sum_i^m a_i b_i = \frac{1}{m} a \cdot b = \frac{1}{m} a^{\top} b\)(嗯,其实最好每个向量都用\(\boldsymbol{a}\)或者\(\vec{a}\)这样的形式表示向量,不过写\(\LaTeX\)真的挺烦的,所以就意会哈)。
现在再假设我们有一组基\(\{u_1, u_2, \dots u_m \}\)可以完全对应原来的维度。那我们希望中心化以后的数据在\(u_1\)方向上散的最开,也就是方差最大。因为我们的数据做了中心化处理,所以我们可以将这个事情用公式表示为\(\frac{1}{n} \sum_i^n(x_i \cdot u_1)^2\)(嗯,这里我又偷懒了,假装我们现在的\(x_i\)都是已经中心化以后的向量)。那这个公式就可以转化为\(\frac{1}{n} \sum_i^n (x_i^{\top} u_1)^{\top} (x_i^{\top} u_1)= \frac{1}{n} \sum_i^n u_1^{\top} x_i x_i^{\top} u_1\)。我们用\(X = [x_1, x_2, \dots, x_n]\)来表示所有的数据,那么因为上面\(u_1\)跟\(i\)无关,因此我们可以将\(u_1\)提到求和符号外面,那我们的公式可以进一步化简为\(\frac{1}{n} u_1 (\sum_i^n x_i x_i^{\top}) u_1 = \frac{1}{n} u_1 XX^{\top} u_1\)。
那么现在问题来了,算到这一步,如何计算能得到一个\(u_1\)使得上式最大呢?我们对公式分解一下发现\(XX^{\top}\)其实非常的眼熟,这不就是原来各个维度的协方差矩阵么,那我们用\(S\)来表示,\(S\)是一个实对称矩阵。那现在我们可以想一下手上有哪些条件,第一我们希望求的是\(\arg \max(u_1^{\top} S u_1)\),同时,因为\(u_1\)是基向量,因此\(u_1^{\top} u_1 = 1\)。那么我们可以建立拉格朗日函数: \[ f(u_1) = u_1^{\top} S u_1 + \lambda(1 - u_1^{\top} u_1) \] 这样我们就可以对\(u_1\)求导数: \[ \frac{\partial f}{\partial u_1} = 2S u_1 - 2\lambda u_1 \] 另上式等0,我们就可以得到\(S u_1 = \lambda u_1\)。更熟悉的来了,这就是矩阵的特征根公式嘛,所以我们可以知道,我们在找的就是原来矩阵的协方差矩阵的特征根,所以很自然的,当我们选择特征值最大的那个特征根的时候,我们的目标值就最大。这样我们就求到了第一个最大的主成分。
那如果我们现在想要做的事情是做多维的PCA的话,那么我们得到第一个主成分,现在要求第二个主成分需要注意什么呢?首先我们希望的事情是:
第二个主成分方向上的方差也是最大的
第二个主成分最好跟第一个主成分是垂直的,因为这样我们可以保证第二个主成分的信息和第一个主成分的信息之间没有重叠。换句话说,可以保证两个成分之间是完全无关的。
那为了达到这样的目的,我们会发现,如果我们让两个成分相互垂直,那么我们其实很容易就会发现,其实这第二个成分也有可能是协方差矩阵的特征向量,而且就是次大的特征值对应的特征向量。当然这种想法是一种想当然的做法,最保险的方式还是用拉格朗日乘子去求解。那第二个主成分的拉格朗日方程就可以协作是\(f(u_2) = u_2^{\top} S u_2 + \alpha(1-u_2^{\top}u_2) + \beta(0-u_2^{\top}u_1)\),然后求偏导一步步得到结果。
那么PCA还剩下最后一个没有解决的问题就是实操的时候,我们要选择留下多少个component呢?这里一般用的方法就是去计算\(\frac{\lambda_j}{\sum_i^n \lambda_i}\),然后我们自己觉得大概累计百分比到什么程度我们可以接受,然后就可以保留多少component。
矩阵分解
那用PCA我们说是在抽取某种pattern,或者说latent factor。但是实际上因为PCA的系数可以正可以负,所以PCA实际上并不能真正抽取到pattern。举个例子来说,如果我们对面部图像进行PCA分解,我们会得到的是如下的图:
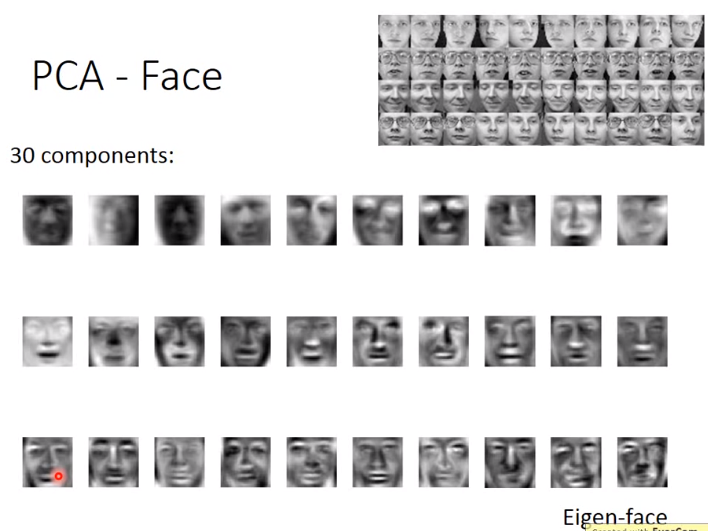
那我们会发现,其实我们没有找到所谓的component,我们反而得到的是各种各样的脸。那其实这是很容易理解的,因为\(x = a_1 w_1 + a_2 w_2 + \dots\),那每一个系数可以是正的,也可以是负的,所以我们得到的每一个principle component其实可以是各种复杂的元素相互组合起来的结果。比如一个component是有胡子,然后系数是负的,刚好就把胡子减掉,然后就还原回原来的脸了。
那么我们为了解决这个问题,真正做到抽component,我们可以强制要求,系数是正的,同时每一个分解的component的元素也都是正的。也就是做NMF,就是non-negative matrix factorization。那我们就可以得到下面的图:

这样我们就会发现,比如有抽出眉毛,下巴之类的。
那matrix factorization有很多种抽法,最常见的就是SVD和NMF。那矩阵分解其实就是在抽取某种latent factor。
比如说下图:
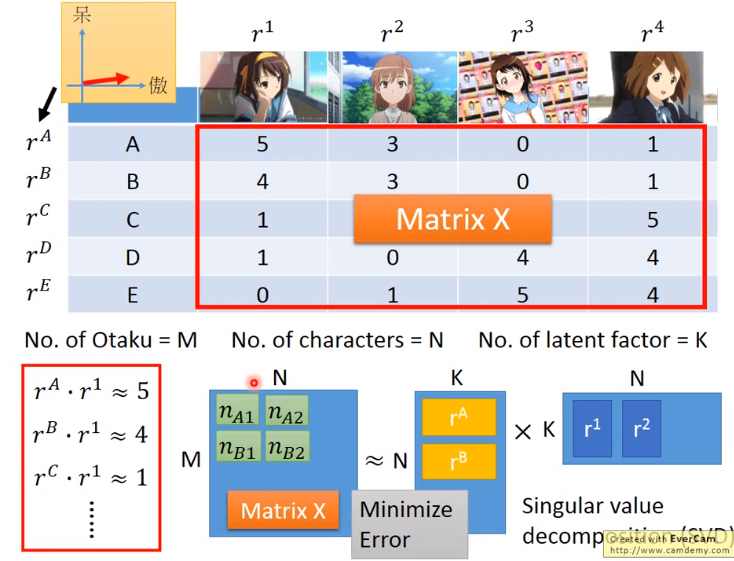
我们手上有一个矩阵,就是每个死宅买的手办个数。那我们就可以用这样的方法将这个大矩阵拆解为两个相乘的矩阵,而这两个矩阵的\(K\)实际上就是latent factor。这里其实课件里有个错误,约等号右边的第一个矩阵应该是M行。
那么我们要怎么解这个公式呢?嗯,一般书上解SVD的方法我表示线代太差,先留着后面再来刚。所以换一条路,我们想要做的事情就让分解后乘回去的矩阵跟原来的矩阵几乎一样,所以我们其实就可以用\(L_2\) norm来做梯度下降。也就是求\(\arg \min \sum_{(i, j)} (r^i \cdot r^j - a_{ij})^2\)。那其实这样把每个元素都加起来,然后用梯度下降来求解就好了。所以看到这里,突然一想,上面PCA其实也可以用梯度下降来做吼。
那上面的做法是只考虑了内在的共同属性,其实有时候某些人就是喜欢买手办,或者说某些手办就是卖得好之类的。那其实这里面就是说可能存在bias。所以我们可以将bias引入,那上面的公式就变成是\(\arg \min \sum_{(i, j)} (r^i \cdot r^j + bias_i + bias_j - a_{ij})^2\)。那其实这就是SVD++算法。既然可以加bias,那就意味着可以加regularization。
那么矩阵分解其实有很多很多的应用。在NLP里面,如果做无监督文档分类会用到一种非常简单的方法叫LSA(latent semantic analysis),那其实就是前面的矩阵分解,只是换了个名字而已。另外现在很流行的topic model用的是LDA,全称是latent dirichlet allocation,其实也是LSA的一种变化。跟线性判别LDA(linear discriminant analysis)是两码事情。不过线性判别需要labeled data。
其他还有很多很多的降维方法,基本上都是各种线性变换。嗯,线代少不了。
