传统机器学习,或者说现在主流的机器学习都是有监督学习,也就是supervised learning。但是实际上,数据好拿,labeled data不好拿。这就是我们为什么要用semi-supervised learning。
semi-supervised learning并不一定总会work,这要看你的假设是否真的会成立。
EM算法
现在我们来看一下半监督模型如何使用在generative model。之前我们学的是supervied learning,都是在labeled data上做的假设,如下图:

那现在我们如果有了其他的unlabeled data,在实践上,我们就不能够用原来labeled data的\(\mu, \Sigma\)。也就是说,这些unlabeled data的分布会影响我们对均值和方差的假设,从而影响我们算posterior probability。

那么我在做semi-supervised generative model步骤如下:
首先初始化参数:\(\theta = \{P(C_1), P(C_2), \mu^1, \mu^2, \Sigma \}\)
其次计算unlabeled data的后验概率:\(P_{\theta}(C_1 | x^u)\)
然后更新模型:\(P(C_1) = \frac{N_1 + \Sigma_{x^u}P(C_1|x^u)}{N}\),其中\(N\)是所有的sample,\(N_1\)是标记为\(C_1\)的样本。那如果不考虑unlabeled data,原来\(C_1\)的概率就是\(\frac{N_1}{N}\)。现在我们因为考虑了unlabeled data,因此我们在计算的时候就需要加上所有unlabeled data属于\(C_1\)的概率。而\(\mu_1 = \frac{1}{N} \sum_{x^r \in C_1} x^r + \frac{1}{\sum_{x^u} P(C_1|x^u)} \sum_{x^u}P(C_1|x^u)x^u\)。然后重复更新后验概率,直到收敛。
这两个步骤,第一个计算后延概率就是计算expectation,更新模型就是做maximization,也就是EM模型。但是这个模型会受到初始化参数的影响,这一点跟梯度下降很像。
那为什么这个模型要这样设计呢?
首先回过头来看极大似然法,在只有labeled data的情况下,likelihood可以写作\(log L(\theta) = \sum_{x^r} log P_{\theta}(x^r, y^r)\),其中\(P_{\theta}(x^r, y^r) = P_{\theta}(x^r|y^r)P(y^r)\)。这个算法,在我们假设的概率分布已知的情况下,很容易就能算出来。
在考虑unlabeled data的情况下,我们的likelihood就可以写作是\(log L(\theta) = \sum_{x^r} log P_{\theta}(x^r, y^r) + \sum_{x^u} log P_{\theta}(x^u)\),其中\(P_{\theta}(x^u) = P_{\theta}(x^u|C_1)P(C_1) + P_{\theta}(x^u|C_2)P(C_2)\)。因为未标注的数据我们不确定到底属于哪一种类别。那EM算法做的事情,就是让这个log likelihood最大。跟极大似然法不一样的地方就是,EM算法只能一次次迭代来逼近最优解。
Low density separation
另外一个semi-supervised learning的方法是self-training。这种方法假设的就是这个世界上的数据只有一种标签,那self-training的方法就是先用labeled data训练数据,然后对unlabeled data进行分类。分类之后我们选择比较confidence的结果加入训练集继续训练模型。但是这里要注意,这个过程实际上不能在regression上起到效果。因为regression输出的就是个real number,而这个predict的值就是原来的函数计算的,所以再放进来也没法对模型起到调优的效果。
self-training有一个进阶版本,也就是entropy-based regularization。这个值用来计算我们预测结果的分布是否集中。也就是说,我们要计算\(\hat{y}^u\)的entropy,也就是\(E(\hat{y}^u = \sum_{m=1}^M \hat{y}_m^u ln(\hat{y}_m^u))\)。那我们希望这个值越小越好。越小,说明值越集中,越大说明越分散。所以我们的loss function就可以从原来的cross entropy改进为\(L = \sum_{x^r}C(y^r, \hat{y}^r) + \lambda \sum_{x^u} E(\hat{y}^u)\)。这个结果就可以用梯度下降来做,另外因为后面加上了unlabeled data的这个尾巴,看上去就像是之前做regularization,所以这里就叫做了regularization。
那这两个方法都属于low density separation,也就是假设这个世界是非黑即白的。
Smoothness assumption
第三种方法就是smoothness assumption。简单说就是如果有两笔数据\(x_1, x_2\),如果他们在high density region是类似的,那么他们的标签应该是一致的。如下图:
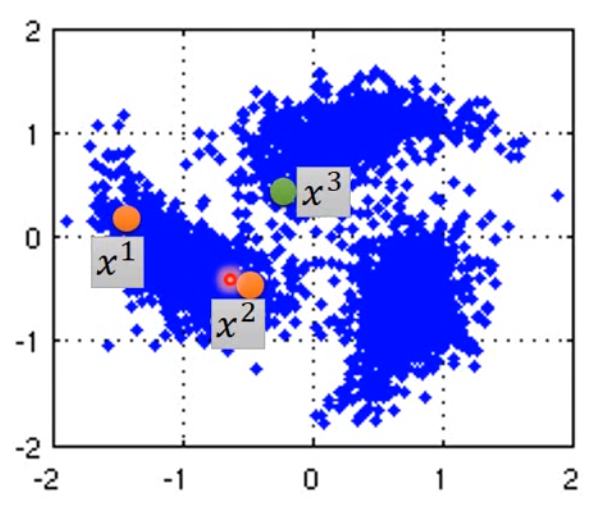
图中的\(x^1\)和\(x^2\)更接近,而\(x^3\)就更远。另一个直观一点的例子就是:
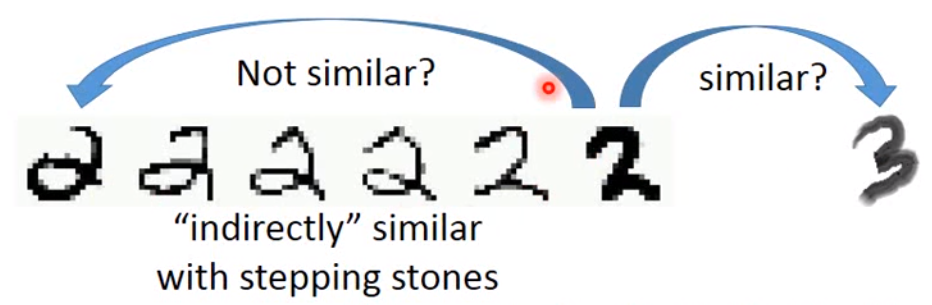
在两个2之间,虽然在像素点上看起来不是很像,但是中间有很多过渡的数据,因此左边两个2是类似的。同时,我们没有2过渡到3的数据,因此右边的2和3很不像。
那实践上,要做到这一点的一种方法就是先做cluster,然后做label。但是实际上,这个做法真正实践起来是比较麻烦的。
另一种方法就是graph-based approach。也就是说两个数据点必须有通道可以到达这样才是距离近的,如果两个数据点之间没有连接,那就是距离远的。这样做一般需要设计好如何计算两个数据点之间的相似度\(s(x^i, x^j)\)。然后我们可以用KNN或者e-neighborhood来添加edge。如下图:
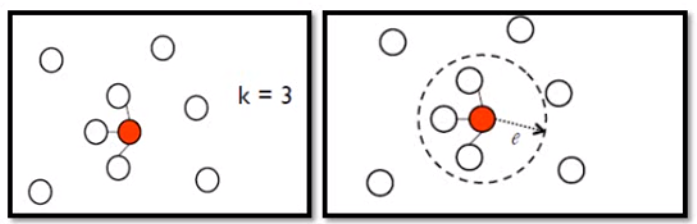
KNN是连接离自己最近的K个点,而e-neighborhood是去连接半径为e内的所有点。
除了添加edge之外,我们可以给edge加上weight,可以用similarity,也可以用RBF(径向基)\(s(x^i, x^j) = exp(- \gamma||x^i - x^j||^2)\)。因为这里用了exponential,因此只有非常近的两点才会有高的similarity。
graph-based的方法的好处是可以将label传递出去,当然这样的做法就需要海量的数据,否则这种连接就可能断掉。如下图:
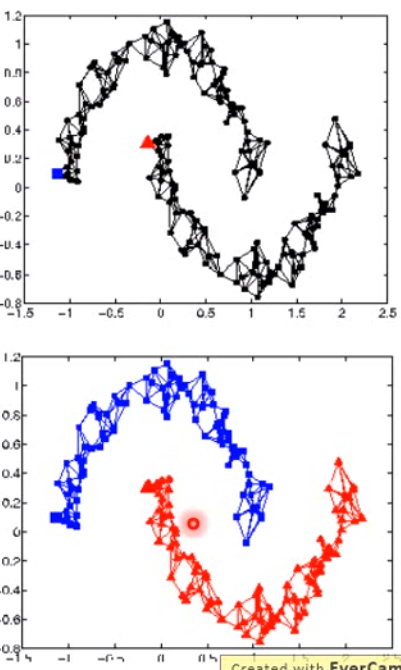
那么如何从数学上来计算这件事情?

如上图,我们定义一个值叫smooth,smooth越小,就越好。这个公式也可以用矩阵的方式来表示: \[ S = \frac{1}{2} \sum_{i,j} w_{i,j}(y^i - y^j)^2 = \boldsymbol{y}^{\top} \boldsymbol{Ly} \] 那这里的\(\boldsymbol{y}\)是包含了labeled data和unlabeled data的一个向量,所以dimension是\(R+U\)。那\(\boldsymbol{L}\)相应的就是一个\((R+U) \times (R+U)\)的一个矩阵。那\(\boldsymbol{L}\)这个矩阵叫做graph laplacian matrix,定义为\(L = D - W\),其中\(D\)是原来graph的邻接矩阵,而\(W\)则是\(D\)的degree组成的对角矩阵。如下图:
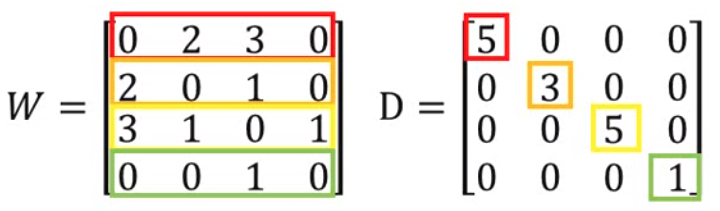
那我们也就可以将这个smooth作为一个惩罚项加入到原来cross entropy这个loss function中,得到\(L = \sum_{x^r} C(y^r, \hat{y^r}) + \lambda S\)。
上面是三种半监督学习的方法。第四种方法是寻找latent factor。这个在后面的无监督学习里讲。
