这节课的内容讲的有点浅,所以我看到是李沐的gluon教程,配合这节课的内容。
Seq2Seq
这个是encode-decode的过程。之前写的LSTM做文档分类是限定了输入的长度。超出规定长度的句子我们是截断,没达到长度的我们是padding。但是用seq2seq可以接受不定长的输入和不定长的输出。
实际上seq2seq是有两个循环神经网络,一个处理输入序列,另一个处理输出序列。处理输入序列的叫编码器,处理输出序列的叫解码器。流程上如下图:
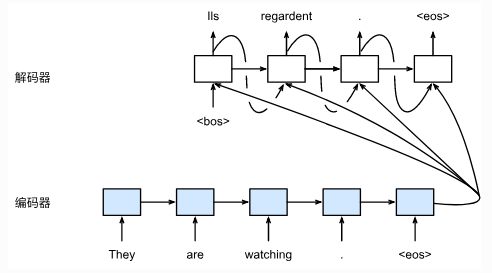
encoder
编码器是将一个不定长的输入序列变换成一个定长的背景向量\(c\)。根据不一样的任务,编码器可以是不一样的网络。例如在对话系统或者机器翻译的场景下,我们用的编码器可以是LSTM,如果在caption的场景下,CNN就是编码器。
现在假设我们做一个机器翻译的任务,那么有一句话可以拆成\(x_1, \dots, x_T\)个词的序列。下一个时刻的隐藏状态可以表示为\(h_t = f(x_t, h_{t-1})\)。\(f\)是循环网络隐藏层的变换函数。
然后我们定义一个函数\(q\)将每个时间步的隐藏状态变成背景向量:\(c=q(h_1, \dots, h_T)\)。
decoder
之前的编码器将整个输入序列的信息编码成了背景向量\(c\)。而解码器就是根据背景信息输出序列\(y_1, y_2, \dots, y_{T'}\)。解码器每一步的输出要基于上一步的输出和背景向量,所以表示为\(P(y_{t'}|y_1, \dots, y_{t'-1}, c)\)。
像机器翻译的时候,我们的解码器也会是一个循环网络。我们用\(g\)表示这个循环网络的函数,那么当前步的隐藏状态\(s_{t'}=g(y_{t'-1}, c, s_{t'-1})\)。然后我就可以自定义一个输出层来计算输出序列的概率分布。
损失函数
一般而言,会用最大似然法来最大化输出序列基于输入序列的条件概率: \[ \begin{split}\begin{aligned} \mathbb{P}(y_1, \ldots, y_{T'} \mid x_1, \ldots, x_T) &= \prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, x_1, \ldots, x_T)\\ &= \prod_{t'=1}^{T'} \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}), \end{aligned}\end{split} \]
因此损失函数可以表示为: \[ - \log\mathbb{P}(y_1, \ldots, y_{T'} \mid x_1, \ldots, x_T) = -\sum_{t'=1}^{T'} \log \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}) \]
beam search
通常情况下,我们会在输入和输出序列前后分别加一个特殊符号'<bos>'和'<eos>',分别表示句子的开始和结束。不过很多时候好像'<bos>'不是必须加的,虽然我觉得不加很奇怪。
假设我们输出一段文本序列,那么输出辞典\(\mathcal{Y}\),大小为\(|\mathcal{Y}|\),输出的序列长度为\(T'\),那么我们一共有\(|\mathcal{Y}|^{T'}\)种可能。
那么如果按照穷举检索,我们要评估的序列数量就是全部的可能性。假设我们有10000个词,输出长度为10的序列,那么我们的可能性就是\(10000^{10}\)这么多种可能性。这几乎是不可能评估完的。
那么换个思路,如果每一次我们都只拿概率最高的那一个词,也就是说每一次拿的是\(y_{t'} = \arg\max_{y_{t'} \in \mathcal{Y}} P(y_{t'}|y_1, \dots, y_{t'-1}, c)\)。只要遇到'<eos>'就停止检索。这就是一个非常典型的贪婪算法。这样的话我们的计算开销会显著下降。
但是贪婪算法会有典型的问题,就是检索空间太小,无法保证最优解。比如下图:
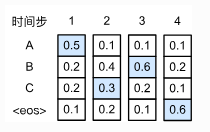
这里的数字表示每一个state,ABC表示每一个词。中间的数字是条件概率,比如B2这里的0.4表示在\(P(B|A)\),而A2就是表示\(P(A|A)\)。如果我们按照贪婪算法的话,我们会得到的结果是ABC,那么概率是\(0.5 \times 0.4 \times 0.2 \times 0.6\),而如果不是贪婪算法的话,我们得到ACB,概率是\(0.5 \times 0.3 \times 0.6 \times 0.6\)明显概率更大。
所以我们为了保证有更大的概率可以检索到较多的可能性,我们可以采用束搜索的方法,也就是说,我们每一次不再只看概率最高的那一个词,而是看概率最高的数个词。我们用束宽(beam size)\(k\)来表示。之后根据\(k\)个候选词输出下一个阶段的序列,接着再选出概率最高的\(k\)个序列,不断重复这件事情。最后我们会在各个状态的候选序列中筛选出包含特殊符号'<eos>'的序列,并将这个符号后的子序列舍弃,得到最后的输出序列。然后再在这些序列中选择分数最高的作为最后的输出序列: \[ \frac{1}{L^\alpha} \log \mathbb{P}(y_1, \ldots, y_{L}) = \frac{1}{L^\alpha} \sum_{t'=1}^L \log \mathbb{P}(y_{t'} \mid y_1, \ldots, y_{t'-1}, \boldsymbol{c}), \] 其中\(L\)是最终序列的长度,\(\alpha\)一般选0.75。这\(L\)的系数起到的作用是惩罚太长的序列得分过高的情况。
事实上,贪婪搜索可以看做是beam size为1的束搜索。过程上就像下图:
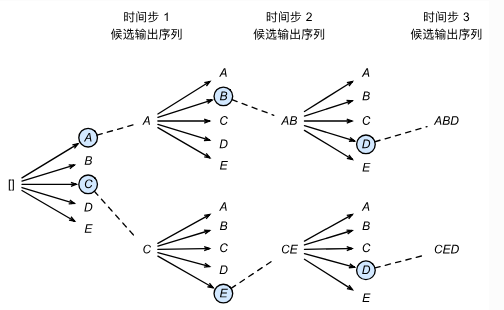
那么不同于贪婪搜索,束搜索其实并不知道什么时候停下来,所以一般来说要定义一个最长的输出序列长度。
Attention
前面说的解码器是将编码器的整个序列都作为背景来学习。那比如说机器翻译里面,我们翻译的时候其实可能没必要全部都看一遍,只要看一部分,然后就可以将这部分翻译出来。比如说“机器学习”翻译为“machine learning”,“机器”对应的是“machine”,而“学习”是“learning”,所以翻译machine的时候只要关注机器就可以了。
其实所谓的关注点,如果用数据来表示也就是权重大小,关注度越高权重越高。如下图:
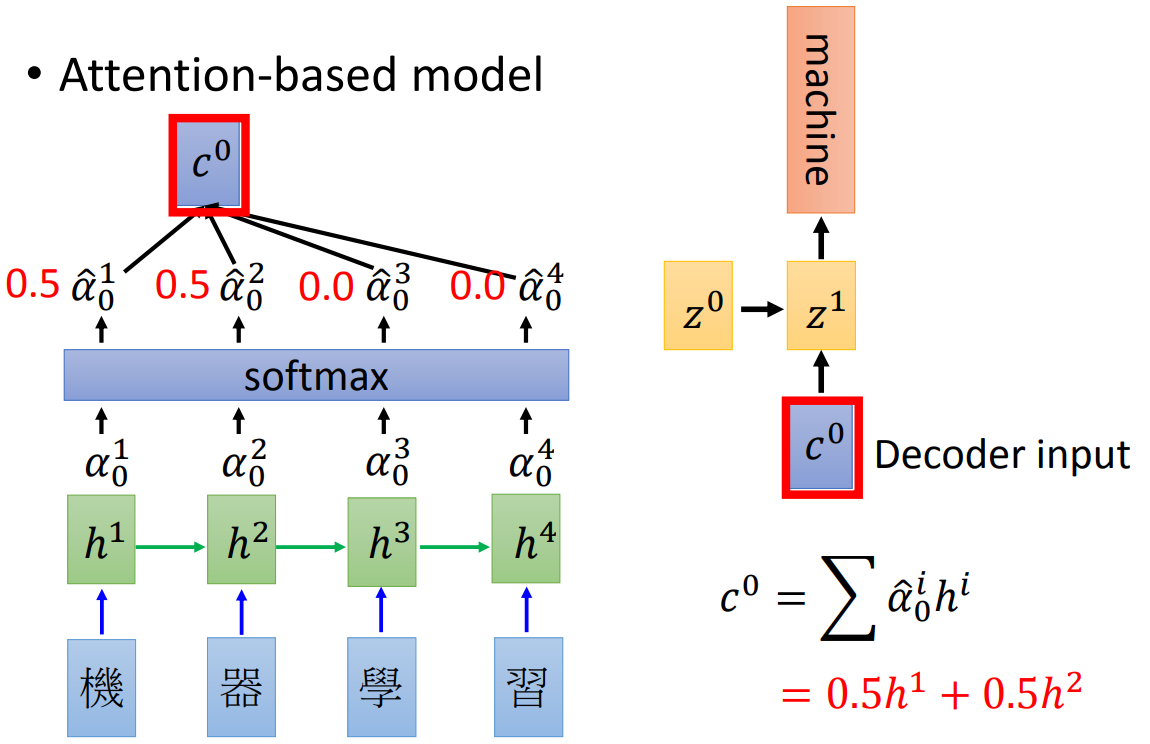
我们在输出背景向量的时候做一个softmax,然后每一个state给一个权重,作为\(t'\)时刻的输入,这样jointly训练就可以学出一个attention的形式。
那么这里的\(\alpha\)是这样计算出来的:
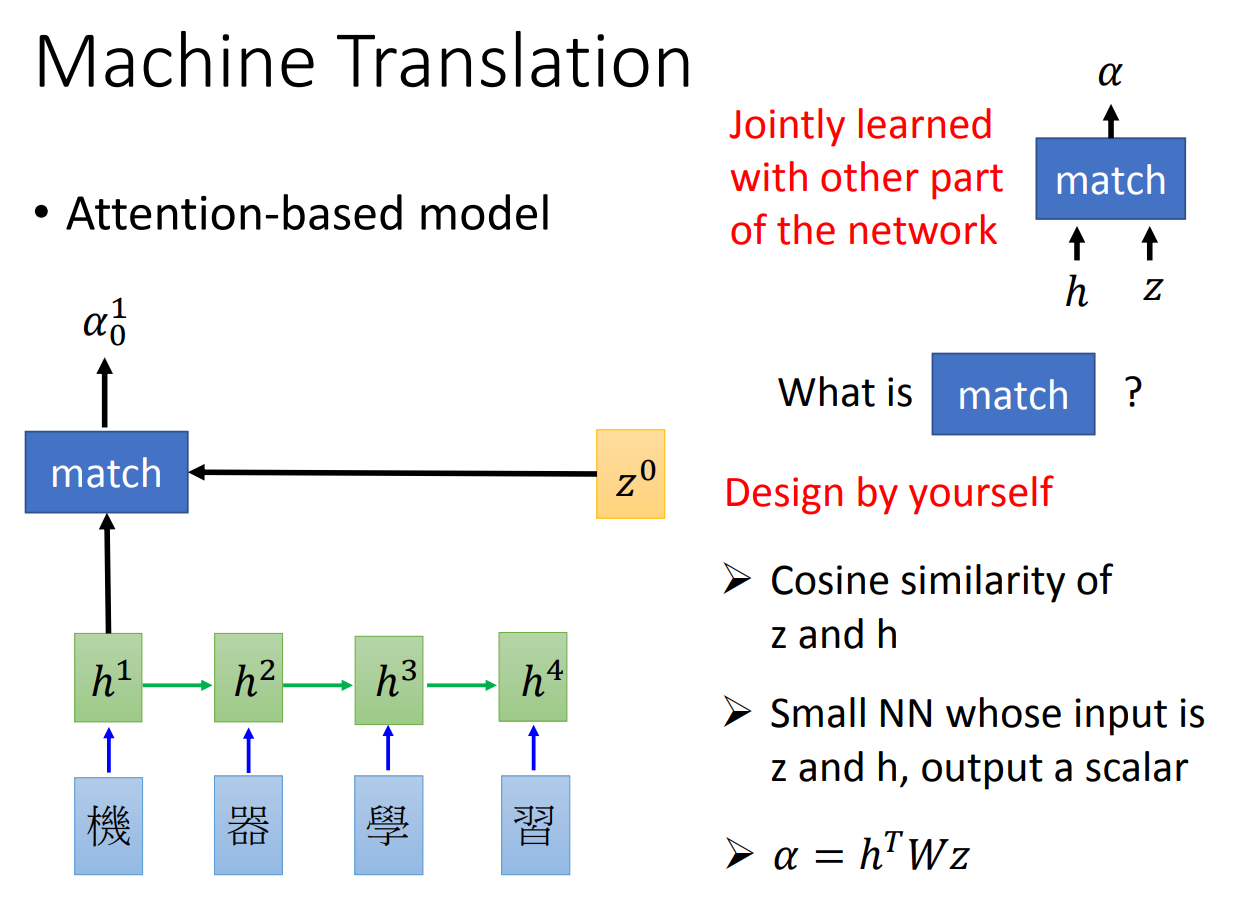
其实就是每一个state的decoder的input拿来和encoder的hidden做一个match。至于match的函数可以自己随意定义。
这样一来,我们就可以让解码器在不同的state的时候关注输入序列的不同部分。
