学习一下batch normalization和SELU,顺便看点深度学习的八卦。
BN
Batch normalization是一个比较新的深度学习技巧,但是在深度学习的实作中有非常迅速成为中流砥柱。
normalization是以前统计学习比较常用的一种方法,因为对于损失函数而言,\(L(y, \hat{y})\)会受到输入数据的影响。这个其实是非常直观的,比如说一个数据有两个维度,一个维度都是1-10的范围内波动的,另一个维度是1000-10000之间波动的,那么如果\(y=x_1 + x_2\)很明显后一个维度的数据对\(y\)的影响非常大。
那么在这种情况下,我们做梯度下降,在scale大的维度上梯度就比较大,但是在scale小的地方梯度就比较小。这个在我之前学梯度下降的博客里面也有。大概图形上看就是下面这样:

那这样我们在不同维度上的梯度下降步长是不一样的。所以在统计学习或者传统的机器学习里面,为了加快收敛的速度,虽然用二阶导可以解决,但是一般用feature scaling就可以了。
而batch normalization其实也是使用了这样的理念。一般而言,我们做normalization就是\(\frac{x-\mu}{\sigma}\),那batch normalization其实就是在每一个layer的input前做这么一下操作。
那batch normalization和normalization的差别其实就在于batch这个地方。我们知道平时我们训练深度学习网络的时候避免炸内存,会将数据分批导进去训练,在这种情况下,我们其实是没有办法得到全局的\(\mu\)和\(\sigma\)的。所以事实上,batch normalization每一次算的都是一个batch的\(\mu \ \& \ \sigma\)。
那整个流程看上去就是下图这样的:
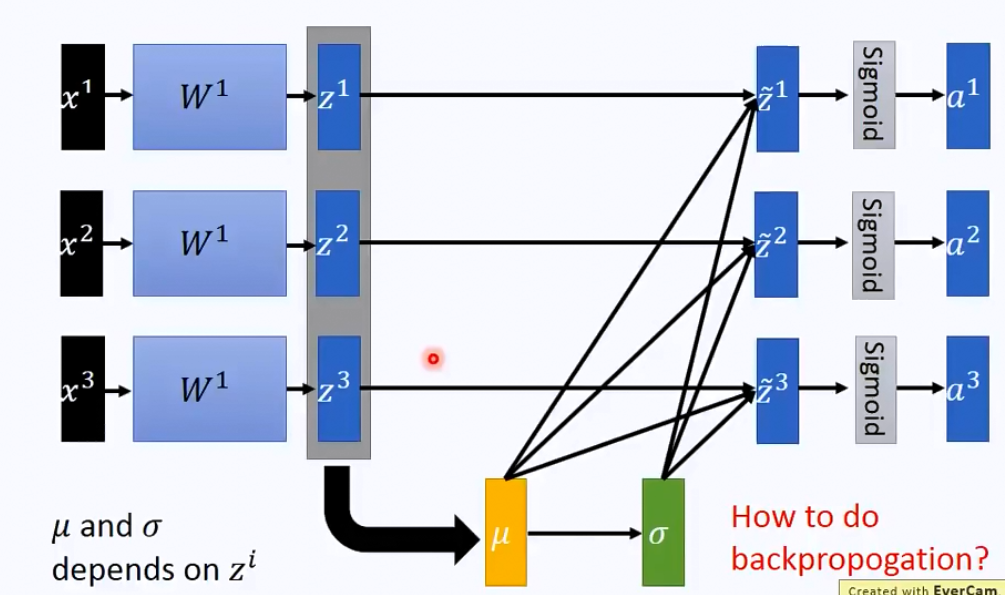
那实际上可以将这个过程看作是一个hidden layer来处理。
如果说觉得这样全部normalization到0,1这样的形式可能有些activation function效果不好,所以我们可以考虑一下再加一层linear layer来转换一下,那流程上就是:
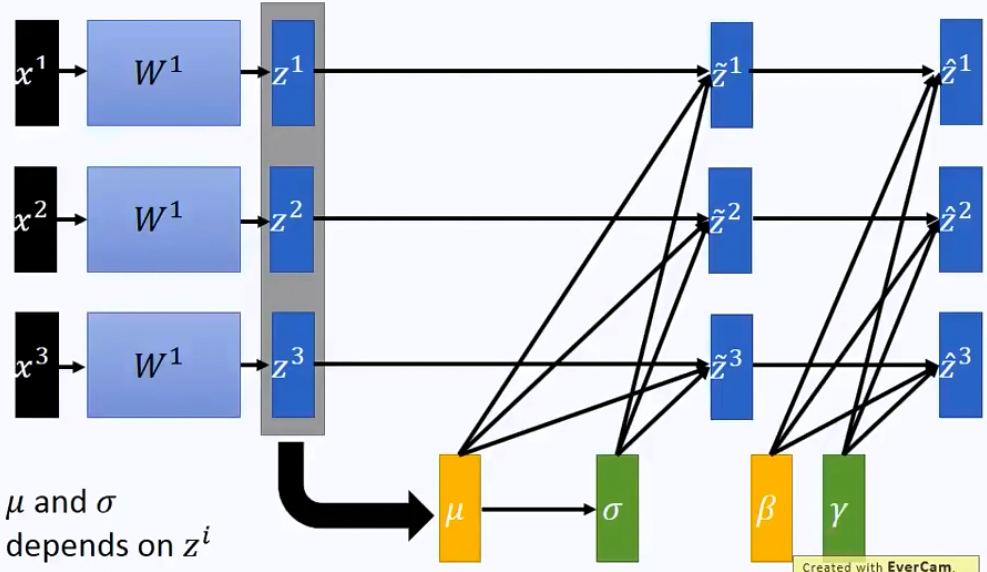
当然,如果好巧不巧,机器学着学着,刚好\(\beta\)和\(\gamma\)跟前面的一样,那么这轮的batch normalization就白做了。不过一般来说不会这么巧。
那么在训练过程中,我们一般都是一个batch一个batch喂进去,但是test的时候,我们一般是一口气全部过模型一遍,那么我们并没有办法得到一个合适的\(\mu\)和\(\sigma\)。那么一种解决方法是计算一下全部training set的均值和标准差,另一种方法是,每次训练后,我们都保留最后一个batch的均值和标准差。
BN的好处非常显而易见,一个是可以减少covariate shift。也就是说,以前为了避免每个layer的方差太大,我们会减小步长,但是用了BN以后就可以用大的步长加速训练。此外,对于sigmoid或者tanh这样的激活函数来说,可以有效减少深层网络的梯度爆炸或者消失的问题。另外BN的一个副产物是可以减少过拟合。
SELU
ReLu是一种比较特殊的激活函数,本身是为了解决sigmoid在叠加多层后会出现梯度消失的问题。ReLu的函数其实非常简单,就是: \[ a = \begin{cases} 0, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \] 不过现在回过头看ReLu,其实某种程度上效果很像是dropout?!
但是ReLu相对来说还是比较激进的,所以后来有各种各样的变种,比如说Leaky ReLu,就是: \[ a = \begin{cases} 0.01z, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \] 还有parametric ReLu: \[ a = \begin{cases} \alpha z, &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \]
再后来在竞赛中还有人提出了randomized relu,其实就是上面的parametric relu的\(\alpha\)每次训练的时候都随机生成一个,而不是让机器去学习,然后test的时候再固定一个就可以了。据说效果还不错。
但是这种形式的ReLu都是负无穷到正无穷的值域,于是又有人修正为ELU(exponential linear unit),函数是: \[ a = \begin{cases} \alpha(e^z - 1), &\mbox{if }z<0 \\ z, &\mbox{if }z>0 \end{cases} \] 这样一来,ELU的值域就是\(\alpha\)到正无穷。
之后横空出世了一个SELU,其实就是ELU前面乘了一个参数\(\lambda\),函数表示为: \[ a =\lambda \begin{cases} \alpha(e^z - 1), & \mbox{if }z<0 \\ z, & \mbox{if }z>0 \end{cases} \] 不过,这里的两个参数是有确定值的,而不是随便学习出来的。这里\(\alpha=1.6732632423543772848170429916717\),\(\lambda=1.0507009873554804934193349852946\)。
这两个非常神奇的数据说是可以推导出来的,有兴趣的同学可以去看一下原文93页的证明。看不下去的可以看一下作者放出来的源码。
那么为什么要定这样两个实数,其实目的是保证每次的layer吐出来的都是一个标志正态分布的数据。
花式调参
最后是现在有的一些花式调参的方法。毕竟实作的时候基本上也就是调参了,菜如我这种也不可能提出什么突破性的方法。
深度学习说白了也就是机器学习的一种,所以传统机器学习中的grid search这种非常暴力的方法当然也适用。不过为了加速搜索,一般会用random search的方法,通常也不会太差。
另外现在有一些非常非常骚气的方法,一种就是learn to learn。其实就是用一个RNN去学习另一个网络的所有参数。看上去就是下图的样子:
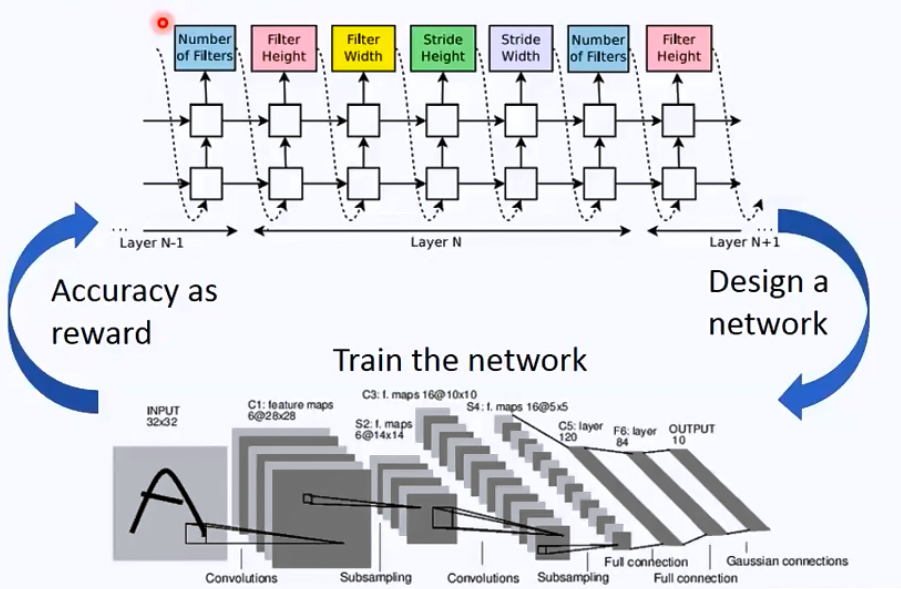
还有一个很重要的调参方向其实就是learning rate,因为深度学习很多时候是一个非凸优化的问题,所以我们以为loss下不去了可能待在了saddle point,实际上也可能是在一个local minimum的山谷里来回震荡。这种时候只要降低lr就可以继续收敛了。所以很多时候我们在训练的过程中,每50个epoch或者100个epoch就缩小一下lr,很多时候loss会出现一次很明显的降低。
最后是Google brain提出了一些非常神奇的激活函数,具体可以看看这篇论文。
深度学习究竟有没有学到东西
这个其实是非常有意思的一个争论点。很多人质疑深度学习其实只是强行记忆了数据的特征,并没有学到潜在的规律。于是有人做了相关的研究,A Closer Look at Memorization in Deep Networks这篇论文就是相关的研究,里面有一个很有意思的地方就是对label加noise。不论加了多少noise,模型都可以train到一个百分百正确的地方。但是test上的表现很自然会变得很差。过程如下图:

这个其实是非常风骚的一个操作,就是说故意给一些错误的信息让机器去学习。这个图里面的实线是train,虚线是test,我们可以看到其实一开始test是上升的,然后才下降。所以实际上一开始模型还是正常学到了一些正确的规律的。但是后面就被噪声带跑偏了。
不过从某种程度上来说,传统的决策树不是更像是强行记住一些东西么。
