卷积网络入门
卷积就是现在活跃在CV领域的大杀器,简写做CNN,实际上是一个fully connected network的变种。
CNN有三个特性:
可以找到图像中特定的pattern,而且这个pattern是比原来的图像要小的。
同样的pattern可以出现在图片中不同的地方,都会被CNN探测到。
可以做subsampling而不会过分影响图像的质量
如图,CNN的做法是这样的:
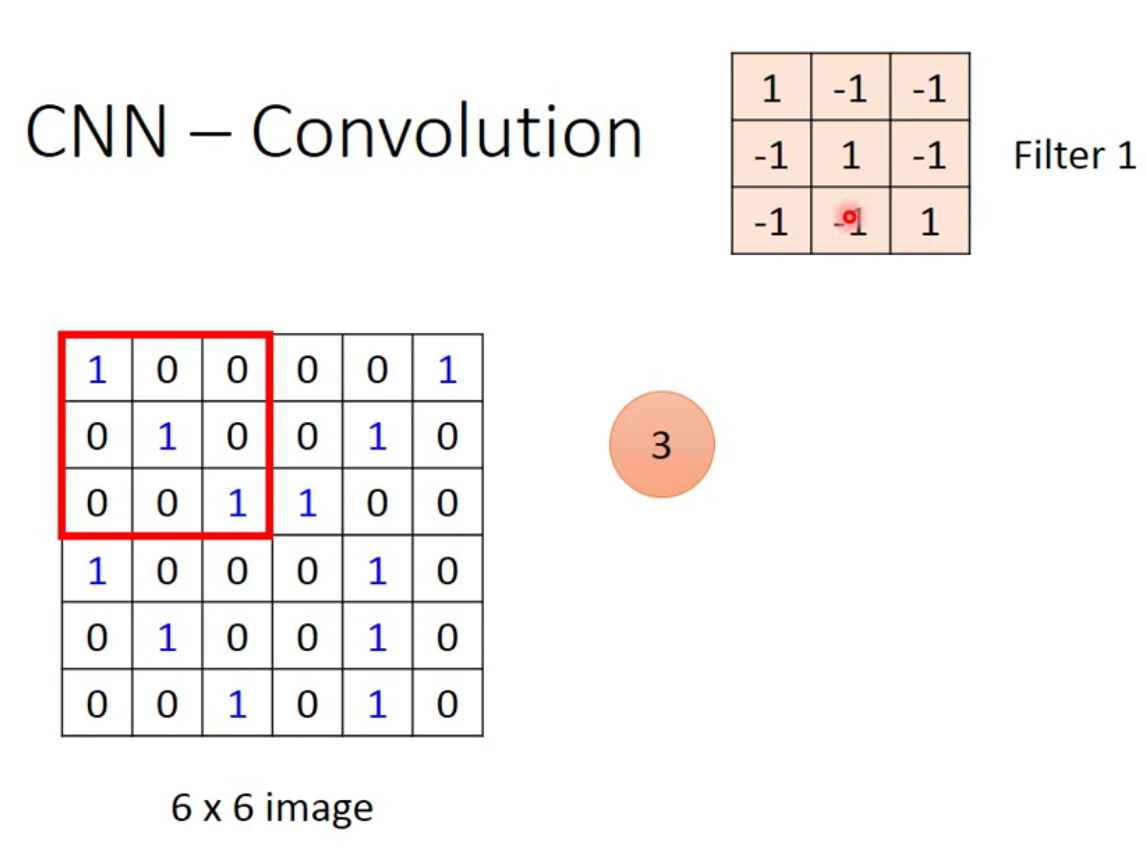
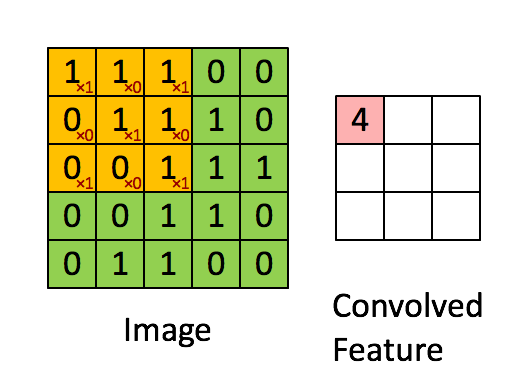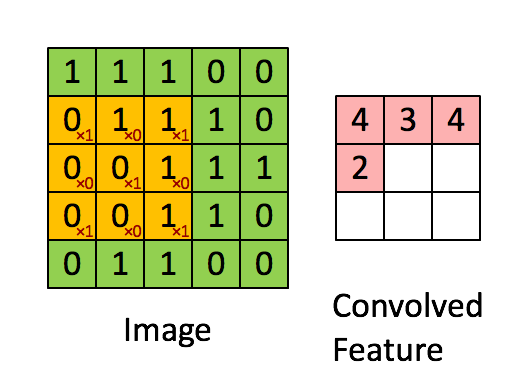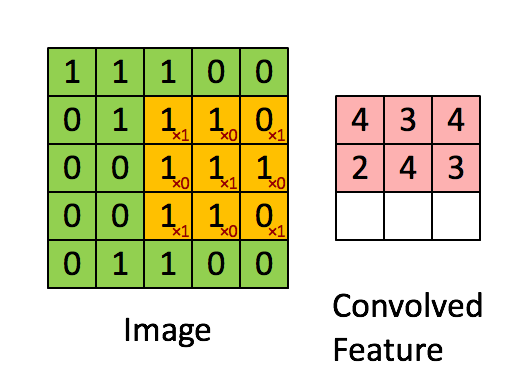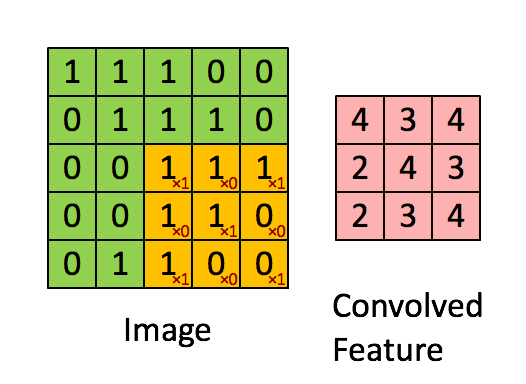
假设我们有一个image如左图,有一个filter如右上角,这个filter是可以被学习出来的。不过filter的大小是需要被人工设定好的,例如这里设定的是\(3 \times 3\)。那CNN的工作原理就是,将这个filter放到image上面,然后等大小的一个matrix跟filter做inner product。所以红色框出来的部分跟filter的内积就是3。
然后我们会移动filter来遍历整个image,这个移动的步伐我们叫做stride,stride的大小表示filter每一次移动的像素数量。例如这里我们stride设为1,那么我们下一步得到的就是下图:
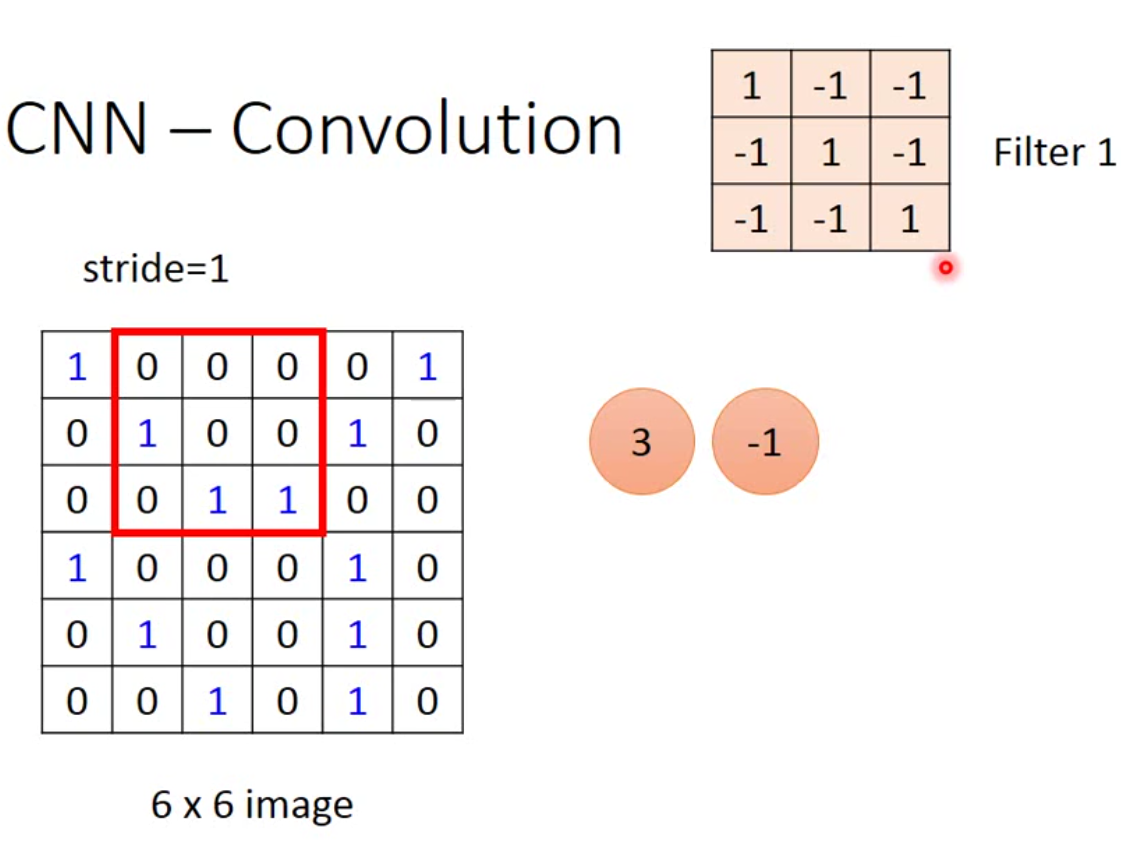
这样一直扫描,直到一排结束,然后向下移动stride的长度再向右继续扫描。
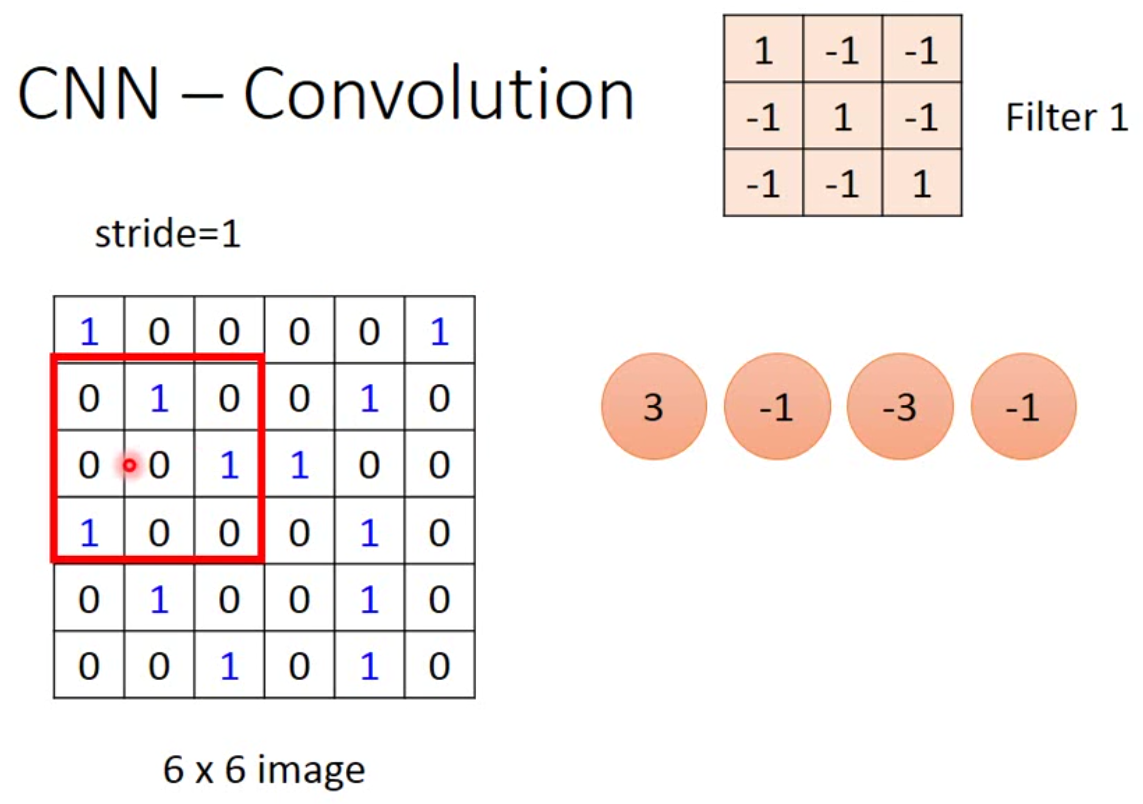
最后我们就能得到这样一个结果:
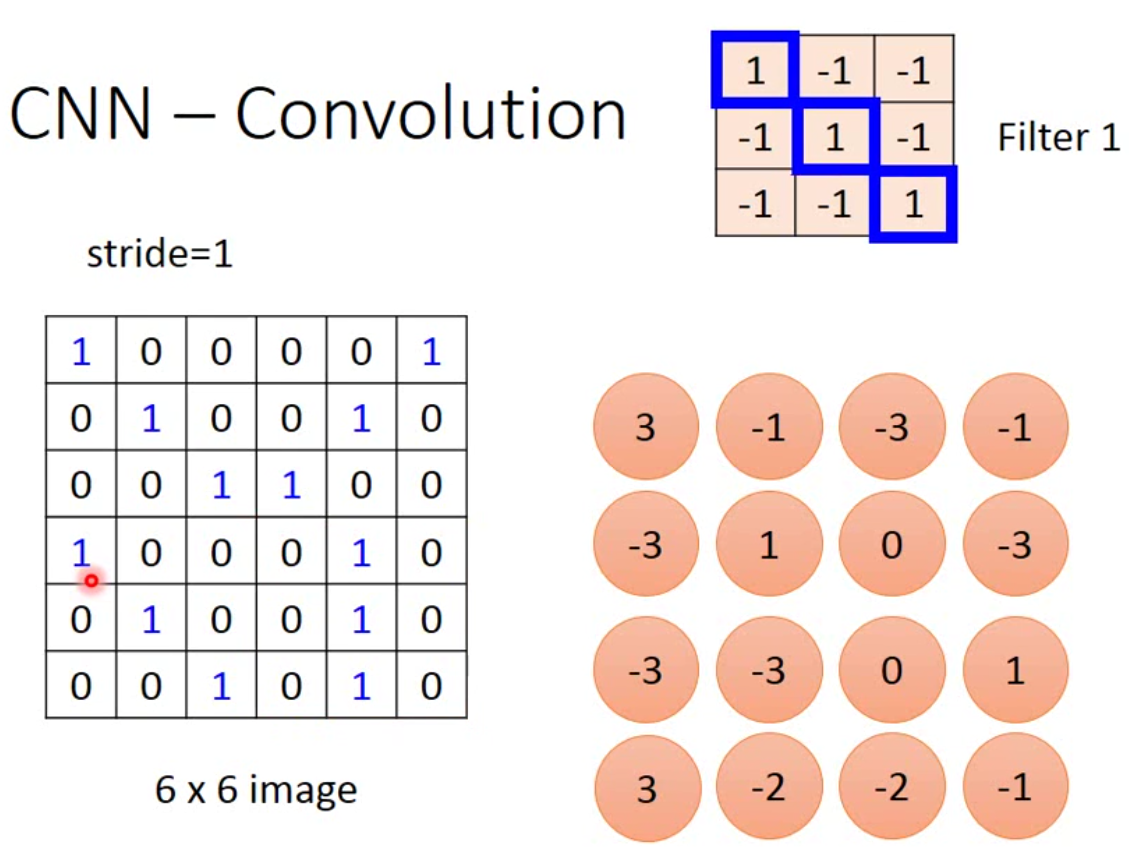
这个filter因为对角线都是1,因此我们这个filter要寻找的就是对角线上的pattern。那么这个image中有两个对角线是1的pattern,一个在左上角,一个在左下角。这就满足了CNN的两个特性。一个是找到一个小于image的pattern,另一个是image中不同位置的pattern可以用一个filter找出来。
我们可以将这个结果看作是经过过滤器处理的新图片,多个filter过滤之后的图片就是feature map。
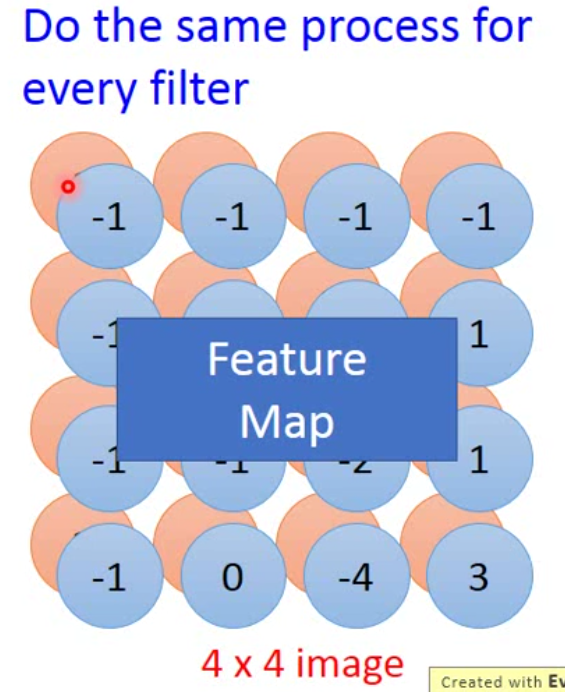
那这个是黑白单通道的图片,如果现在用的是彩色图片,实际上就是拆开为Red、Green、Blue三通道。整个做法如下图:
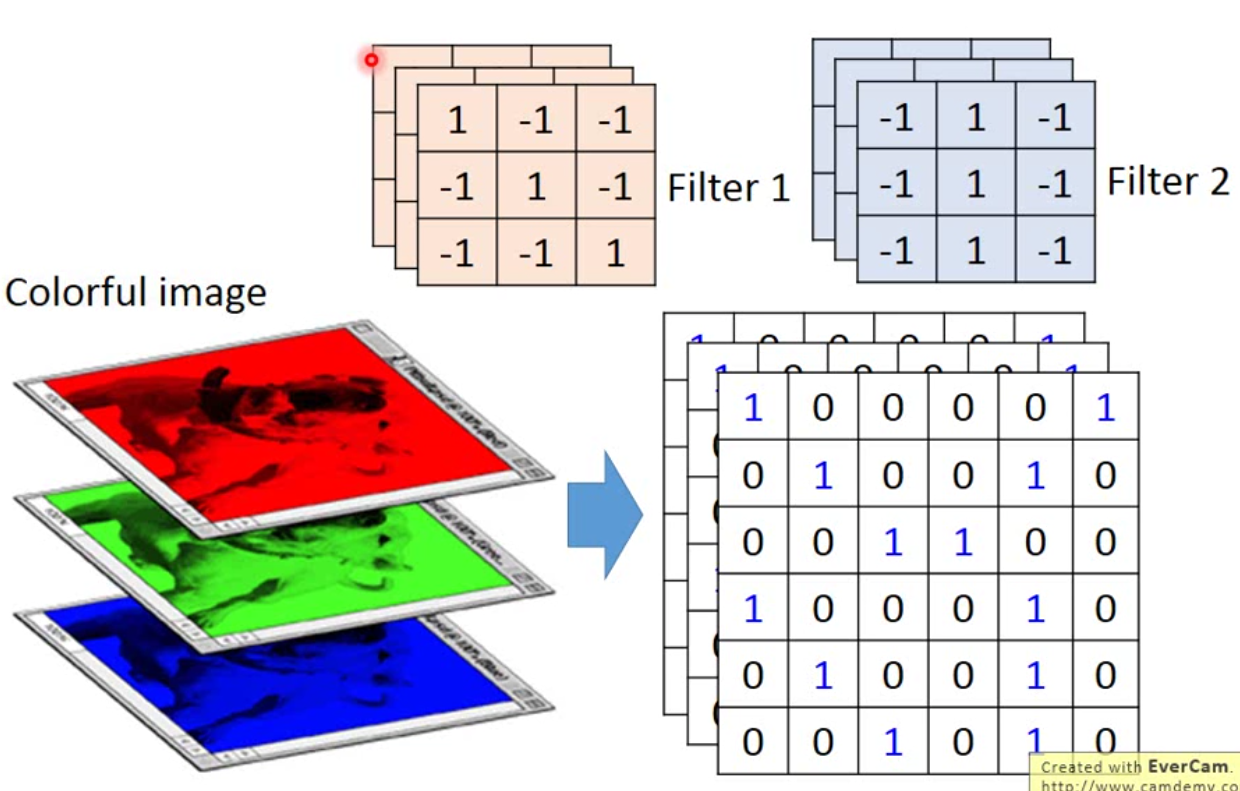
下面一个动图比较形象:
那为什么我们认为卷积是一个特殊的fully connected network呢?
我们现在想象将一个image摊平,从一个matrix摊平成一个vector。我们上面的\(6 \times 6\)的矩阵就可以摊平为一个长度为36的vector。这样我们每个filter的作用就可以用下图来表示:
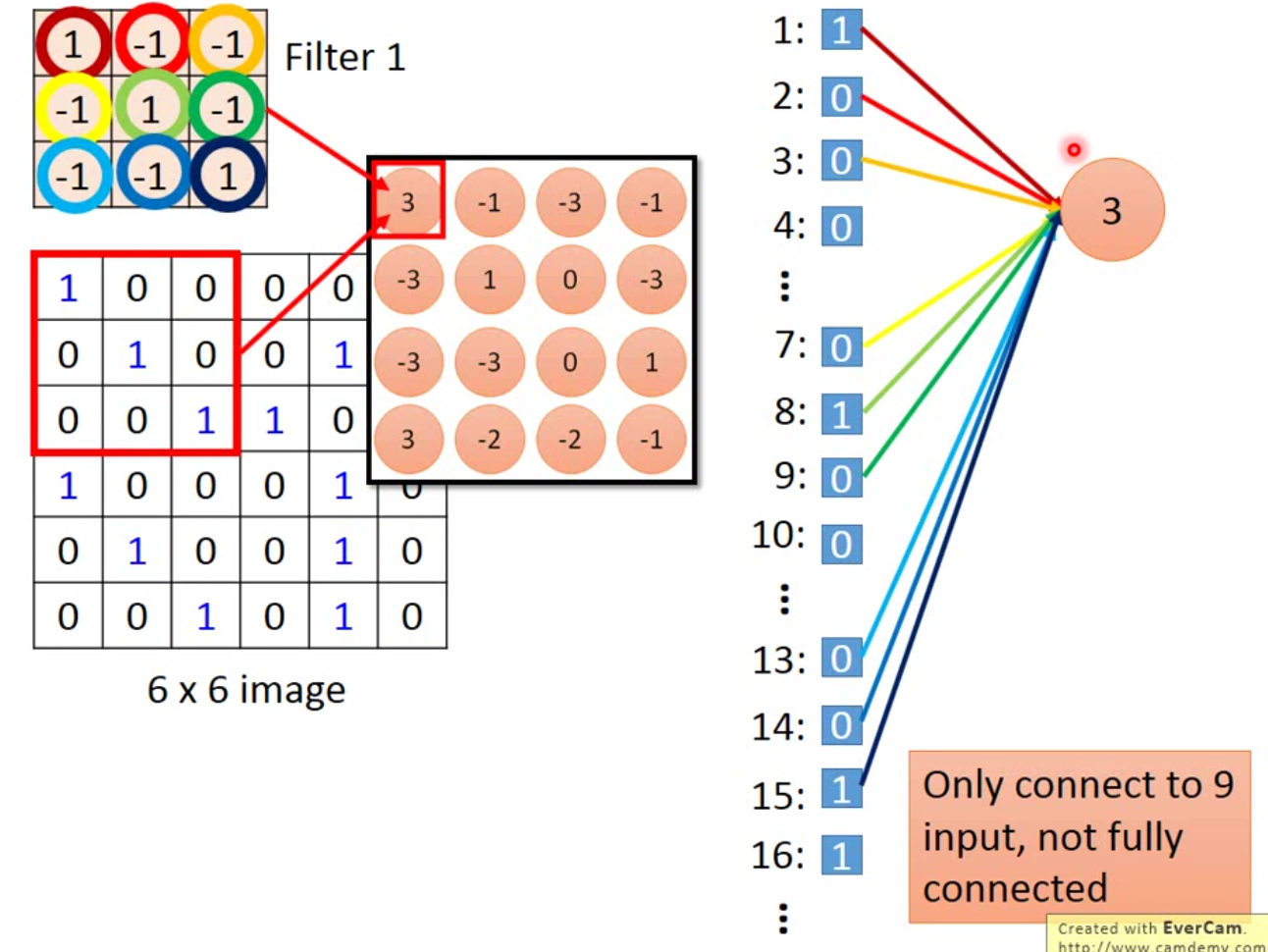
这样的设计有很多好处,首先,我们需要训练的参数远远小于全连接层,如果原来是全连接,我们需要训练36个参数,而现在我们只需要9个。其次,同一个filter移动的时候,参数是一样的,如下图:
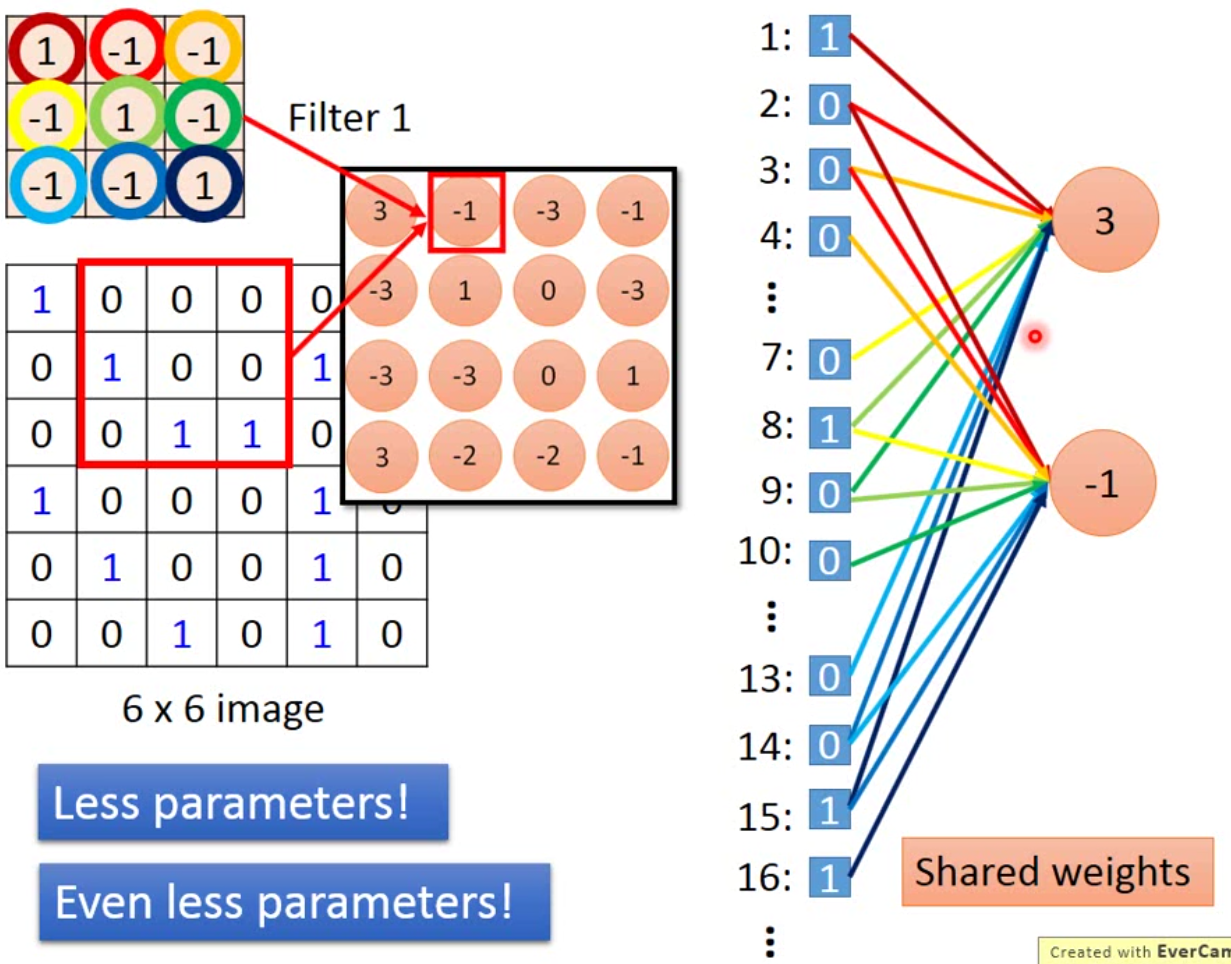
这样的好处同样是减少了需要训练的参数。如果是全连接层,现在接了2个neuron,我们需要训练的参数是72个,而在卷积里面,我们还是只需要训练9个。如果后面filter连接的越多,减少训练参数的效果越明显。
那卷积提取完特征之后,我们会过一个subsampling的过程,也就是pooling的过程。这个过程当中当前有两种常用的方法,一种是average pooling,一种是max pooling。
max pooling的过程就是下图:
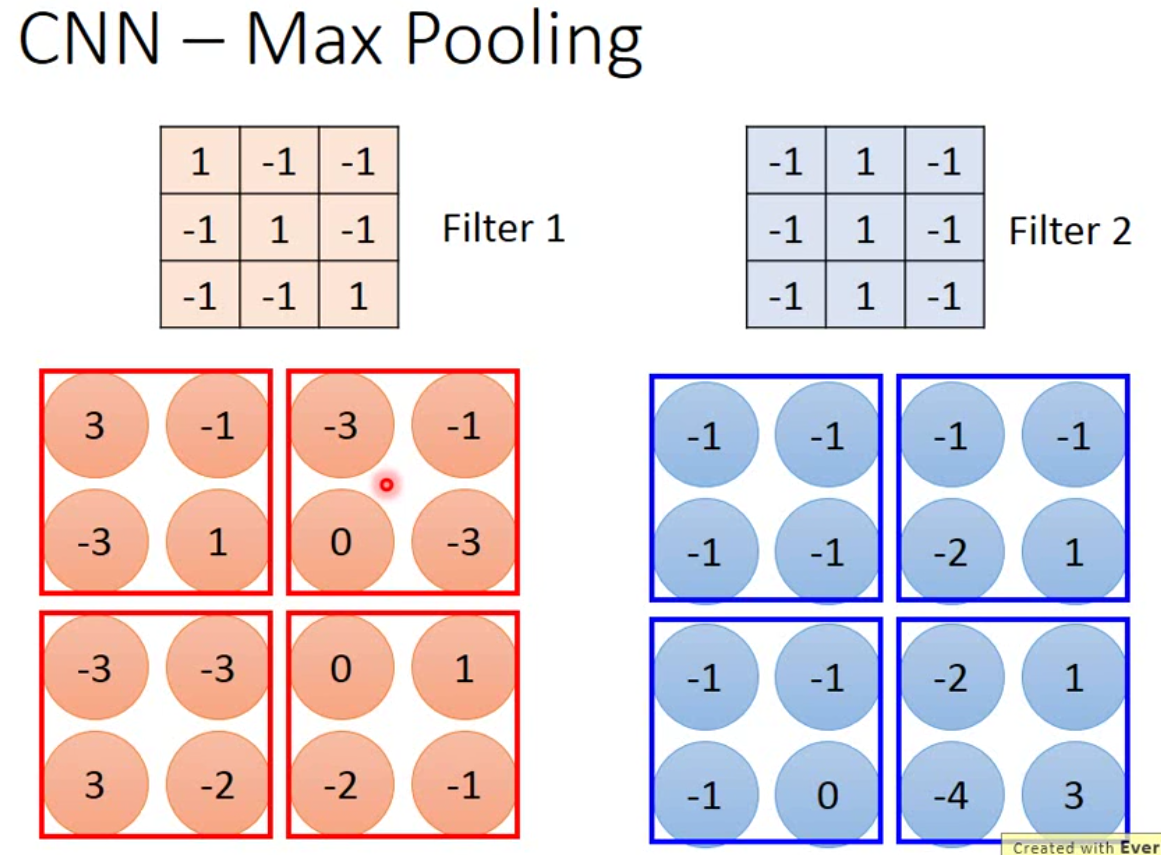
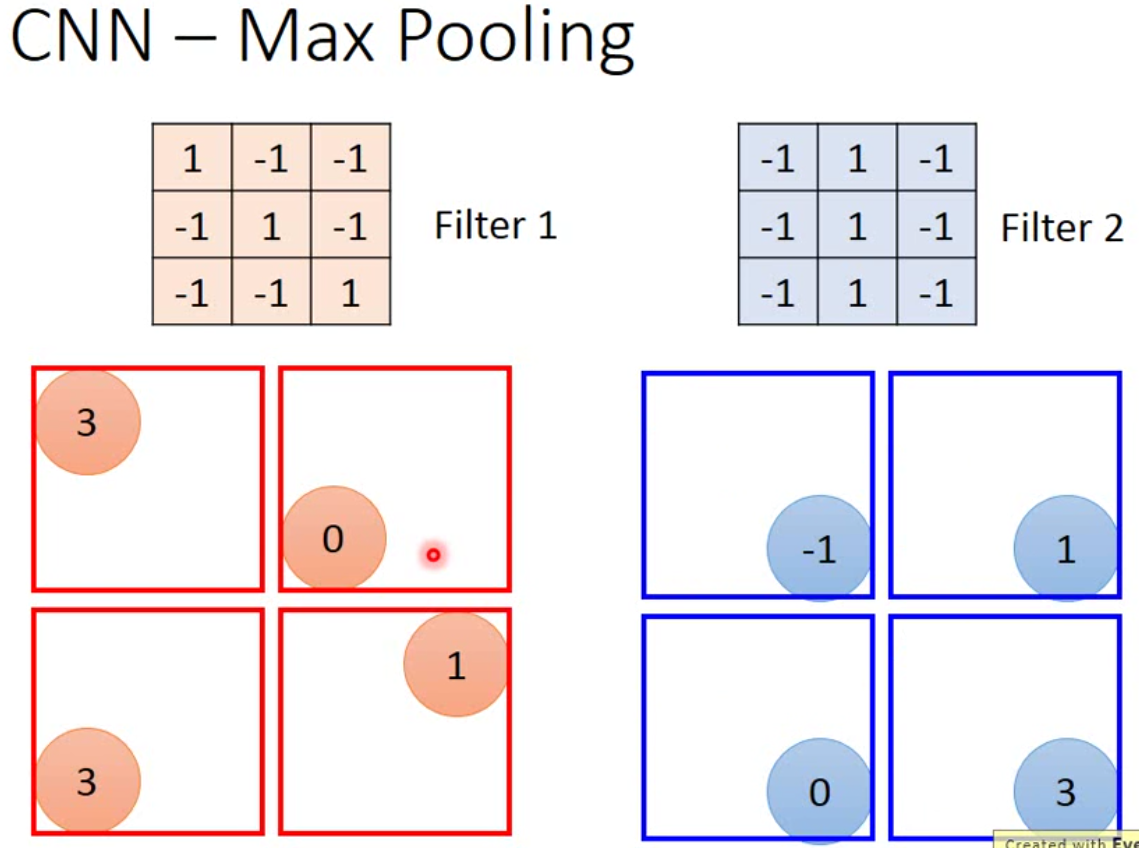
这里我们需要设定的是每一次pooling的窗口有多大,也就是在多大的一个区域内做subsampling,上图设定的大小是\(2 \times 2\)。当然,这里可以用average,也可以用max,也可以两个都用。但是实践上,max的效果好像比average要好一点。那事实上,现在的框架中,pooling层也有stride。
根据要做的事情不一样,不管是filter还是pooling,不一定非要将窗口设定为长宽相等的,也可以是不同的,比如filter也可以设计为\(2 \times 1\)的矩阵这样。另外卷积的过程也可以反复进行好几次。比如VGG-16就有16层卷积。
另外需要提一点的就是,用现在的方法做卷积,原始图片的边边角角会丢失掉,如果filter设计的越大,丢失的就越多。那么为了避免丢失,有一种做法是filter设计的小一点,另一种就是把图片的边边角角拼一段像素上去。拼像素的方法在这里就叫做padding,有几种常见的方法,一种是填0,另一种是将边边角角的像素直接复制一个填进去。那padding要拼多少像素可以根据filter大小来定。filter越大,需要拼的就越多。padding是不是一定比不做效果好,这个视情况而定,多炼丹才知道。
那做完卷积后,我们需要做一个flatten的步骤,也就是将矩阵摊平成向量。如下图:
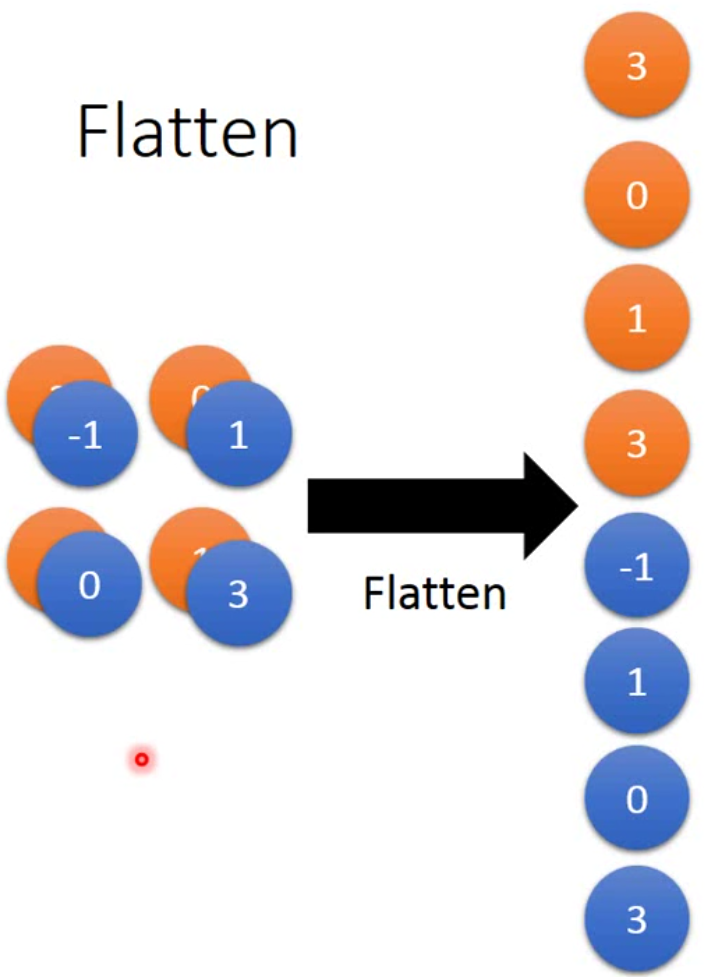
这样的结果最后就可以过fully connected network做分类或者回归了。当然,现在深度学习做分类的还是比较多的。
我们现在可以看一看CNN到底在做什么,下图是AlexNet第一个layer的参数:

这个图我们可以看到,上面的filter主要是看是否有一些pattern存在,而下面则是侦测颜色。事实上有各种各样的可视化方法,比如我们也可以把每个layer的output拿出来做图。
还有一种方法来看CNN是如何work的。例如我们想要分析更高层次layer,我们可以定义一个指标,degree of the activation of the k-th filter: \[ a^k = \sum_i^m\sum_j^n a_{ij}^k \] 我们希望当input一个image(用\(x\)表示)的时候,可以让\(a^k\)最大。也就是\(x^* = \arg \max_x a^k\)。举例来说,如果做了一个识别猫狗的分类器,从仿生的角度而言,我们可以认为一张猫的照片,可以让一个识别猫的特征的神经元兴奋,而识别狗的神经元静默。
那这个公式就可以求导用梯度下降来做这个事情。也就是计算\(\frac{a^k}{x_{ij}}\)。如下图就是这样的效果:
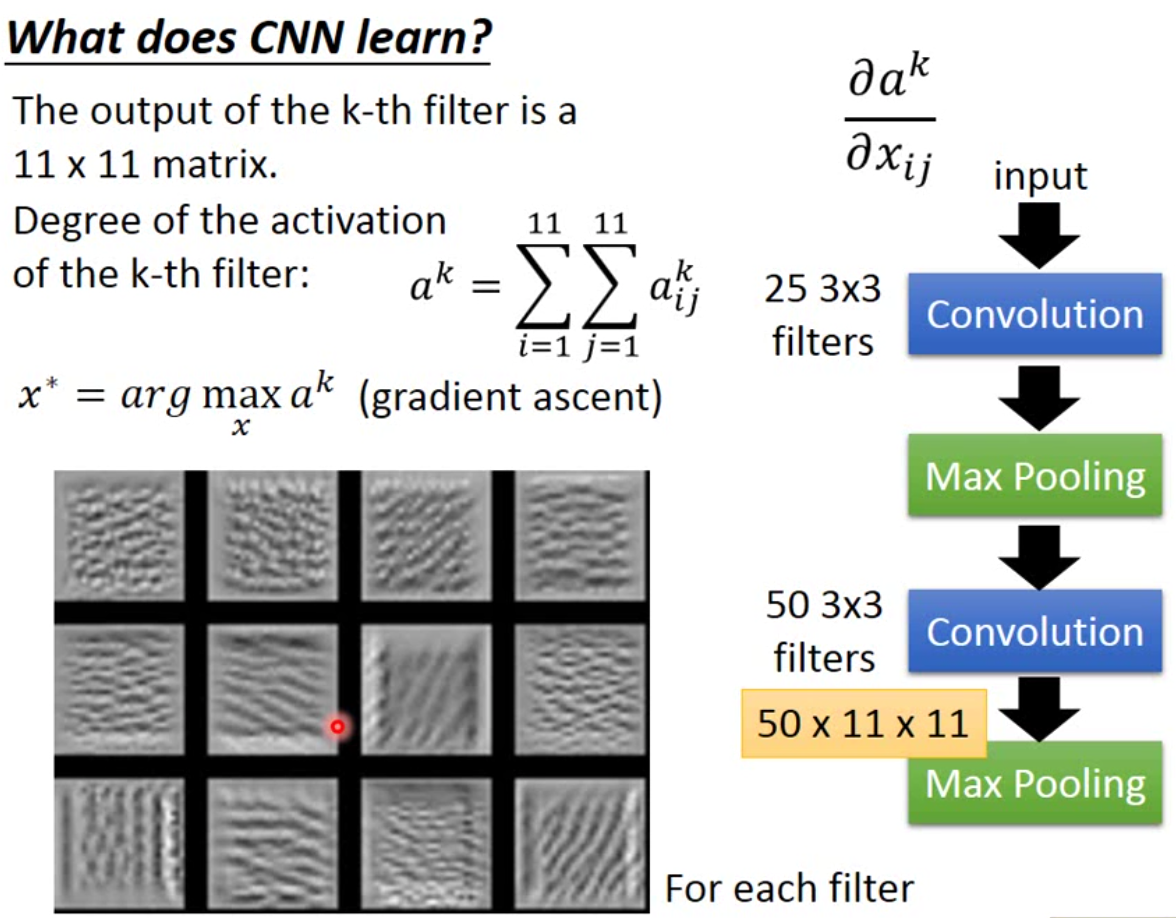
但是在CNN中,如果输出最后一层output的image,实际上我是得不到我们想象中的图片。比如说如果我们做mnist的分类,最后一层输出的图片并不会是数字,很可能得到的就是一片上世纪老电视的雪花屏。所以这样的结果是很容易被欺骗的,也就有了对抗样本这样的存在。另外就是网上有不少介绍的,将同一张图片变换一些像素,就会被识别为别的,比如把熊猫识别成汽车之类的。
那如果我们做一些regularization,比如\(x^* = \arg \max_x (a^k + \sum|x_{ij}|)\),这样最后一个layer的输出相对会规则一点。
当然我们还可以用另一个方式来看CNN到底是不是work的,比如我们取image中某个pixel,\(x_{ij}\),计算\(|\frac{\partial y_k}{\partial x_{ij}}|\),如果这个值很大,那么这个pixel是很重要的。将每个pixel算出来,我们就能知道模型到底聚焦在图片的哪个部分。如下图:
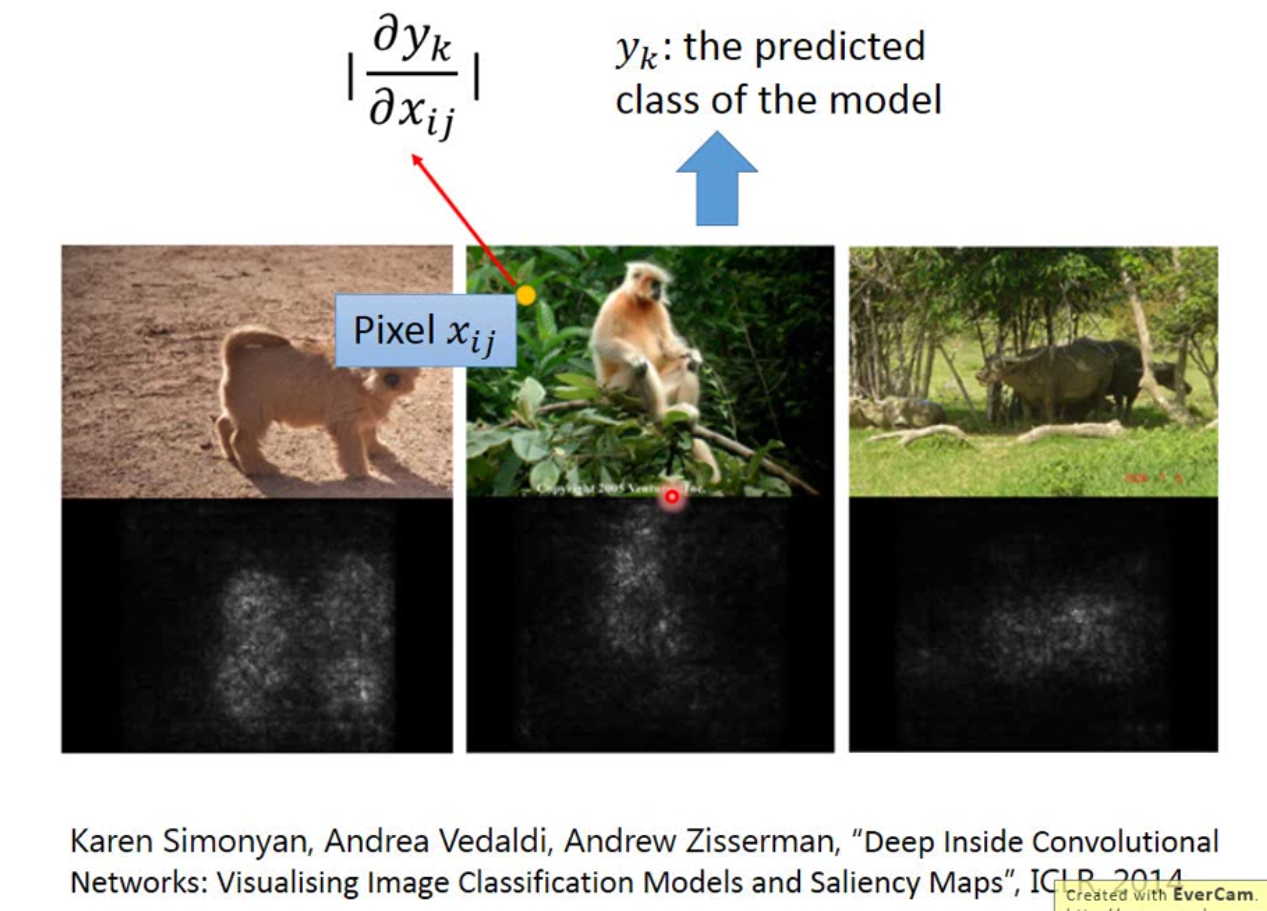
那另外一种简单一点的方法是用一个纯色的框挡掉一些image,这样就能判断模型是不是无法正确识别,这样也能达到类似的效果。比如识别狗的模型,就挡掉狗,不挡掉狗分别试一下模型是不是可以正确分类。
CNN入门大概就这些,应用场景非常的多,反正还是那句话,多炼丹,多开脑洞。
