碎碎念

好久不更新，四月重新开始！

DBSCAN & OPTICS

Posted on Edited on In
Symbols count in article: 7.6k Reading time ≈ 7 mins.

我如期来更新啦！！！聚类算法是很常用的一种算法，不过最常见的就是KMeans了，虽然很多人都会用，不过讲道理，如果是调用现成机器学习库里面的KMeans的话，我敢保证90%的人答不上来具体的是什么算法。相信我，库里的KMeans跟教科书讲的那个随机取初始点的KMeans不是一个算法哟～

因为KMeans依赖K，但是我怎么知道K要用多少呢？另外，KMeans受限于算法本身，对于球状的数据效果较好，但是不规则形状的就不行了。这种情况下，相对而言，基于密度的聚类算法就比较好用了。sklearn里面现在是放了一个DBSCAN，下一版会更新OPTICS。刚好最近都用了，这里把DBSCAN跟OPTICS算法复现一遍。

DBSCAN

DBSCAN算法的原始论文是96年的这篇《A Density-Based Algorithm for Discovering Clusters in Large Spatial Database with Noise》。

DBSCAN是一种基于密度的聚类算法，也就是说，密度高的区域自动聚成一类。这样一来，我们就避免了人为去设定群组数量的问题，算法可以自动发现群组数量。另外用这种方法，如果一个sample不在高密度区域，就有可能被判定为异常值，那么也可以拿来作为异常值检验的方法。

DBSCAN的思路非常简单，有两个参数，一个是\(\varepsilon\)，另一个是minimum points。这里首先定义DBSCAN的几个核心概念，一个是\(\varepsilon\)-neighborhood，另一个是core object，还有就是reachable。

首先是\(\varepsilon\)-neighborhood。DBSCAN开始的时候会随机选取一个初始点，然后按照\(\varepsilon\)的距离寻找临近点，这些点的集合叫做\(\varepsilon\)-neighborhood。参数里面的minimum points就是限定这个点的集合的。minimum points限定了这个集合最小需要包含多少样本点，\(\varepsilon\)则是限定了要用多大的范围去框定这些样本点。这里有个小细节要注意，那就是，算neighborhood的时候，中心点自己是算进来的。

那么这样圈完一波neighborhood后，我们会将符合样本数量大于等于minpts的中心点叫做core object。而core object跟这些neighbor就是reachable的。

然后为了让算法运作起来，只要neighborhood这个集合里面有点，我们就不断重复这样圈地的动作，然后把中心点从集合中拿掉，直到neighborhood为空。

那我们很自然就会想到，一定会圈到一些点，它们不是core object，但是也在集合里面。这些点我们叫做border，也就是说，这些点是这个类的边界了。那么我们就很自然会想到，也有一些点压根不在neighborhood里面，也不是core的点，这些点就是noise。那既然样本点多了两个状态，reachable的情况也就变得多了，如果是直接可以在neighborhood里面找到的，我们叫做directly-reachable；如果通过neighborhood一层层找，最后找到的，我们叫density-reachable。

可以看图说话：

这个图里面，A是core，B、C是border，N是noise。A跟B、C都是density-reachable。但是有没有发现，B是没法返回去找到A的。所以这种reachable是有方向的。

如果对SNA有点了解的朋友就知道，就是一度人脉和N度人脉，但是是一个有向图。

那么算法思路理清了，代码就好写了，这里我就用最常用的欧氏距离了。有人可能会想，如果还是欧氏距离，那跟KMeans还有什么分别，都是画圈圈嘛！请回想一个微积分，只要圈画的够小，就能做出各种形状来。下面是核心部分的代码，详细的可以去看我的notebook。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def _euclidean_dist(p, q):
    return np.sqrt(np.power(p - q, 2).sum())


def _eps_reachable(p, q, eps):
    return _euclidean_dist(p, q) < eps


def _eps_neighborhood(data, point_id, eps):
    neighborhood = []
    point = data[point_id]
    for q in range(len(data)):
        if _eps_reachable(point, data[q], eps):
            neighborhood.append(q)
    return neighborhood


def _is_core_object(neighborhood, minpts):
    if len(neighborhood) >= minpts:
        return True
    else:
        return False


def dbscan(data, eps, minpts):
    class_id = 0
    class_label = np.full(len(data), -1)
    for p_id in range(len(data)):
        if class_label[p_id] == -1:
            neighborhood = _eps_neighborhood(data, p_id, eps)
        if _is_core_object(neighborhood, minpts):
            class_label[neighborhood] = class_id
            neighborhood.remove(p_id)
            while len(neighborhood) > 0:
                current_p = neighborhood[0]
                current_neighborhood = _eps_neighborhood(data, current_p, eps)
                for n in current_neighborhood:
                    if class_label[n] == -1:
                        class_label[n] = class_id
                        neighborhood.append(n)
                neighborhood = neighborhood[1:]
            class_id += 1
    return class_label

OPTICS

那么DBSCAN本身是一个非常牛逼的算法，它解决了我们找K的问题，这样在海量群组的时候，我们不用像KMeans一样去到处尝试K的大小。但是DBSCAN有个问题，那就是这个算法只能检测一个密度。换句话说，如果现在存在一个数据集有两个类，一个类是方差小的，一个类是方差大的。且这两个群组离得不算太远。如果我们为了照顾方差大的群组将eps设得很大，minpts设得很小，那么可能把两个类聚在一起。反过来，我们就可能找不到方差大的类。

那么问题来了，有没有办法量化这个距离呢？三年后，同一组作者在DBSCAN的基础上进化出了OPTICS算法。

既然是DBSCAN的进化版，所以很多概念上都是互通的，只是OPTICS算法多了几个概念，一个是core-distance，一个是reachability-distance。

我们知道，DBSCAN是不断跑马圈地的一个过程，但是我们很直观想就知道，有些密度大的地方，可能不需要\(\varepsilon\)那么大的范围就可以圈到minpts个样本，所以在OPTICS算法里面，我们将满足minpts这么多样本点的\(\varepsilon'\)叫做core-distance。而reachability-distance就是中心点与临近点的距离，但是，如果临近点落在\(\varepsilon'\)内，reachability-distance就用core-distance来替代。如下图：

那么用OPTICS的时候我们就需要定义两个列表，一个是seeds，一个是ordered result。seeds就是我们每一轮迭代时候的候选列表，而ordered result就是最终的结果。

具体的过程是这样的。我们先找到一个点，然后一样跑马圈地，接着计算reachability-distance，然后放到seeds里面从小到大排序。每次取第一个seed出来继续圈地，把被取出来的点以及这个点的reachability distance存在ordered result里面。接着就跟DBSCAN一样，不断重复，直到neighborhood为空。这样做的好处就是，我们可以量化评估每个群的密度大小。效果如下图：

那么我们又会想到，有些seeds里面的点可能随着核心点的移动，reachability distance会不断变小。因为A的core distance里可能是B，而C不在A的core distance里面，但是C在B的core distance里面。如果第一个处理的点是A，第二个处理的点是B，那C其实还是很核心的一个点。那这种时候我们就要跟一它开始的reachability distance做比较，如果新的reachability distance比原来的小，就把原来的值替换掉。

那么废话不多说，上代码，很多地方跟DBSCAN是可以复用的，我就放了一些OPTICS的核心部分，老规矩，详细见notebook：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
def _eps_neighborhood(data, point_id, eps):
    neighborhood = []
    rdist = []
    point = data[point_id]
    for q in range(len(data)):
        dist = _euclidean_dist(point, data[q])
        if dist < eps:
            neighborhood.append((q, dist))
    neighborhood = np.array(neighborhood, dtype=[('id', 'i'), ('dist', 'f')])
    neighborhood = np.delete(neighborhood, np.where(neighborhood['id'] == point_id))
    return neighborhood


def _update_order_seeds(neighborhood, minpts, reach_dists, processed, seeds):
    if not _is_core_object(neighborhood, minpts):
        return seeds
    core_dist = np.sort(neighborhood['dist'])[minpts - 2]
    for obj in neighborhood['id']:
        if not processed[obj]:
            obj_dist = neighborhood[neighborhood['id'] == obj]['dist'][0]
            newRdist = max(core_dist, obj_dist)
            if np.isnan(reach_dists[obj]):
                reach_dists[obj] = newRdist
                seeds[obj] = newRdist
            elif newRdist < reach_dists[obj]:
                reach_dists[obj] = newRdist
                seeds[obj] = newRdist
    return seeds


def optics(data, eps, minpts):
    processed = np.array([False] * len(data))
    core_dists = np.full(len(data), np.nan)
    reach_dists = np.full(len(data), np.nan)
    ordered_res = []
    seeds = {}
    for p_id in range(len(data)):
        if not processed[p_id]:
            ordered_res.append(p_id)
            processed[p_id] = True
            neighbors = _eps_neighborhood(data, p_id, eps)
            if _is_core_object(neighbors, minpts):
                core_dists[p_id] = np.sort(neighbors['dist'])[minpts - 2]
            seeds = _update_order_seeds(neighbors, minpts, reach_dists, processed, seeds)
            while len(seeds) > 0:
                nextId = sorted(seeds.items(), key=operator.itemgetter(1))[0][0]
                del seeds[nextId]
                processed[nextId] = True
                ordered_res.append(nextId)
                newNeighbors = _eps_neighborhood(data, nextId, eps)
                if _is_core_object(newNeighbors, minpts):
                    core_dists[nextId] = np.sort(newNeighbors['dist'])[minpts - 2]
                    seeds = _update_order_seeds(newNeighbors, minpts, reach_dists, processed, seeds)
    # 这里只是我的一个操作，强迫症看不惯有个nan存在。
    reach_dists[ordered_res[0]] = core_dists[ordered_res[0]]
    return ordered_res, reach_dists, core_dists


def cluster_optics_dbscan(data, eps_reachable, eps, minpts):
    orders, reach_dists, core_dists = optics(data, eps, minpts)
    n_samples = len(data)
    labels = np.zeros(n_samples, dtype=int)
    far_reach = reach_dists > eps_reachable
    near_core = core_dists <= eps_reachable
    labels[orders] = np.cumsum(far_reach[orders] & near_core[orders])
    labels[far_reach & ~near_core] = -1
    return labels, orders, reach_dists, core_dists

OPTICS的优点就是，不管是什么形状的密度，基本上都可以把这个凹槽给跑出来，但是问题就是最后的这个抽取群组小算法。目前我还没找到一个比较好的方法来自动抽取，如果是按照论文里面的分层抽取，我试过会抽的太细，如果是按照论文里面的DBSCAN来抽，就是我实现的这个，不过是一刀切的方式，太复杂的样本效果就不好了。目前还在探索用其他平滑方法来替代，有突破再来更新。

试了两种平滑方式，最后的做法是，先用一维高斯平滑，然后用max filter抹掉因为高斯平滑最大值向左漂的问题。

HDBSCAN

然后又发现了一个新的聚类算法，类似OPTICS算法，叫HDBSCAN，顾名思义，就是H就是hierarchical。事实上就是OPTICS算法的一个改进版本。

与OPTICS类似，HDBSCAN一样要算core distance和reachability distance。这个算法跟OPTICS是一样的。但是reachability distance的公式是：\(d_{\text{reach}-k}(a, b) = \max\{\text{core}_k(a), \text{core}_k(b), d(a, b)\}\)，这里的\(d(a, b)\)是两个点用距离公式算的距离。如下图所示：

蓝绿两点直接的reachability distance就是绿点的core distance，红绿两点的就是红绿两点的距离。

那么这样一来，就可以得到每个点之间的reachability distance。然后就可以用这个距离作为权重来绘制一个带权重的连接图。Beyond Hartigan Consistency这篇论文认为，无论是那种概率密度分布，这种相互距离可以更好的表示单链接聚类的层次结构。

然后可以用Prim算法构建最小生成树，然后转化为层次结构，就类似层次聚类了。这个可以参考一下基于最小生成树的层次聚类。然后通过设定最小簇大小，对这个树进行剪枝。也就从下面的第一个图变成第二个图：

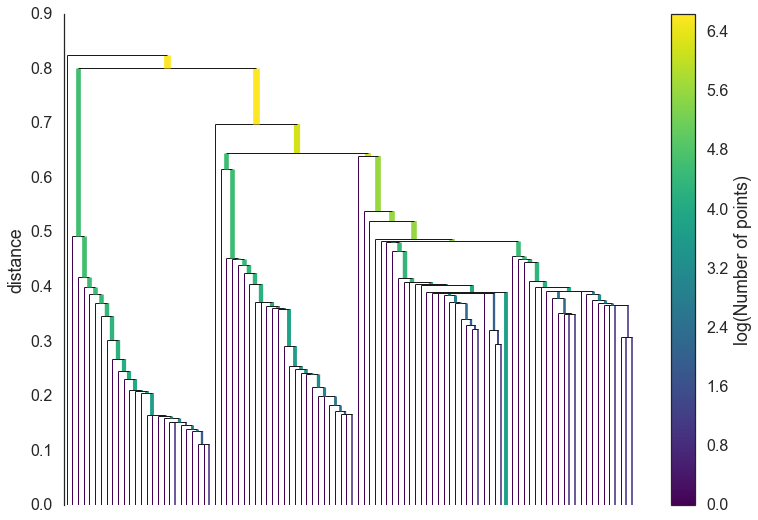
之后就是抽取簇。上面剪枝后的树其实已经有了结果，但是我们希望抽的簇可以自动抽取，且是稳定的。因此我们需要一种度量方式来衡量簇的稳定性。我们定义一个值\(f(x) = \lambda = \frac{1}{\text{distance}_{\text{core}}}\)。这里的distance就是一个点。所以用\(\lambda_{\text{birth}}\)和\(\lambda_{\text{death}}\)分别表示簇生成和簇分裂时候的\(\lambda\)大小，也就是\(\lambda_{\text{min}}C_i\)和\(\lambda_{\text{max}}C_i\)，那么簇的稳定性就是\(S = \sum_{p \in \text{cluster}} (\lambda_p - \lambda_{\text{birth}})\)，\(\lambda_p = \lambda_{\text{max}}(x, C) = \min(f(x), \lambda_{\text{max}}C)\)每轮优化的方向就是让这个稳定性最大，同时满足最小簇大小。

那么HDBSCAN跟DBSCAN比的话，DBSCAN实际上就是上面剪枝前的hierarchical tree切一刀，而HDBSCAN会自适应地去寻找合适的划分。